广东省深圳市南山区2022年三月份中考模拟数学试题
试卷更新日期:2022-04-18 类型:中考模拟
一、单选题
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 下列事件中,是必然事件的是( )A、掷一枚质地均匀的骰子,掷出的点数不超过6; B、一个射击运动员每次射击的命中环数; C、任意买一张电影票,座位号是2的倍数; D、早上的太阳从西方升起3. 有以下说法:
①△ABC在平移的过程中,对应线段一定相等;②△ABC在平移过程中,对应线段一定平行;③△ABC在平移过程中,周长保持不变;④△ABC在平移过程中,对应角分别相等.正确的是( )
A、①②③④ B、①③④ C、②③④ D、①②③4. 一双皮鞋现在售价为100元,比原价降低了20%,则原价为( )A、元 B、元 C、元 D、元5. 对于函数y=2x+1下列结论错误的是( )A、它的图象必过点(1,3) B、它的图象经过一、二、三象限 C、当x> 时,y>0 D、y值随x值的增大而增大6. 把一根长7m的钢管截成2m和1m长两种规格的钢管(每种钢管的数量都不为0),一共有几种不同的截法( ).A、1种 B、2种 C、3种 D、4种7. 如图,在Rt△ABC中,直角边BC的长为m,∠A=40°,则斜边AB的长是( )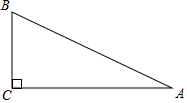 A、msin40° B、mcos40° C、 D、8. 已知抛物线y=ax2+bx+c与反比例函数y= 的图象在第一象限有一个公共点,其横坐标为1,则一次函数y=bx+ac的图象可能是( )A、
A、msin40° B、mcos40° C、 D、8. 已知抛物线y=ax2+bx+c与反比例函数y= 的图象在第一象限有一个公共点,其横坐标为1,则一次函数y=bx+ac的图象可能是( )A、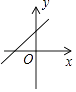 B、
B、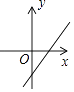 C、
C、 D、
D、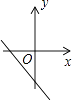 9. 下列运算正确的是( )A、 B、 C、 D、10. 直角三角形的两条直角边的长分别为6和8,则斜边长为( )A、10 B、5 C、4 D、3
9. 下列运算正确的是( )A、 B、 C、 D、10. 直角三角形的两条直角边的长分别为6和8,则斜边长为( )A、10 B、5 C、4 D、3二、填空题
-
11. 如图,已知∠ABC与∠DCB互补,AC⊥BD,如果∠A=40°,那么∠D的度数是 .
 12. 已知直线的解析式为y=ax+b,现从﹣1,﹣2,﹣3,4四个数中任选两个不同的数分别作为a、b的值,则直线y=ax+b同时经过第一象限和第二象限的概率是.13. 当代数式的值等于 , 则代数式的值为 .14. 一个圆锥的母线长为5,高为4,则这个圆锥的侧面积是 .15. 如图,点D(0,6),O(0,0),C(8,0)在⊙A上,BD是⊙A的一条弦,则cos∠OBD= .
12. 已知直线的解析式为y=ax+b,现从﹣1,﹣2,﹣3,4四个数中任选两个不同的数分别作为a、b的值,则直线y=ax+b同时经过第一象限和第二象限的概率是.13. 当代数式的值等于 , 则代数式的值为 .14. 一个圆锥的母线长为5,高为4,则这个圆锥的侧面积是 .15. 如图,点D(0,6),O(0,0),C(8,0)在⊙A上,BD是⊙A的一条弦,则cos∠OBD= . 16. 如图,一条光线照在坡度为1:的斜坡上,被坡面上的平面镜反射成与地面平行的直线,求这条光线与坡面的夹角α
16. 如图,一条光线照在坡度为1:的斜坡上,被坡面上的平面镜反射成与地面平行的直线,求这条光线与坡面的夹角α
三、解答题
-
17. 计算(1)、先化简,再求值:(2x+3)(2x-3)-4x(x-1)+ , 其中x=2.(2)、先化简代数式(1-) , 再从-2≤a≤2范围中选一个恰当的整数作为a的值代入求值.18. 在一次数学活动中,小明设计了一个配紫色的游戏.游戏规则是:在一个不透明的袋子里装有除颜色以外其它均相同的3个小球,其中有2个红球,1个蓝球.甲先从袋中随机摸出1个小球,乙再从袋中剩下的两个小球中随机摸出1个小球.若摸出的两个小球的颜色恰好能配成紫色(红色和蓝色可以配成紫色),则甲获胜;否则乙获胜(1)、用树状图或列表法求出甲获胜的概率;(2)、你认为这个游戏公平吗?请说明理由19. 如图,以BC为直径的⊙O交△CFB的边CF于点A,BM平分∠ABC交AC于点M,AD⊥BC于点D,AD交BM于点N,ME⊥BC于点E, , cos∠ABD= , AD=12.
 (1)、求证:△ANM≌△ENM;(2)、求证:FB是⊙O的切线;(3)、证明四边形AMEN是菱形,并求该菱形的面积S.20. 某开发公司生产的960件新产品需要精加工后才能投放市场.现有甲、乙两个工厂都想加工这批产品,已知甲厂单独加工这批产品比乙工厂单独加工完这批产品多用20天,而甲工厂每天加工的数量是乙工厂每天加工数量的 , 甲、乙两个工厂每天各能加工多少个新产品?21. 如图
(1)、求证:△ANM≌△ENM;(2)、求证:FB是⊙O的切线;(3)、证明四边形AMEN是菱形,并求该菱形的面积S.20. 某开发公司生产的960件新产品需要精加工后才能投放市场.现有甲、乙两个工厂都想加工这批产品,已知甲厂单独加工这批产品比乙工厂单独加工完这批产品多用20天,而甲工厂每天加工的数量是乙工厂每天加工数量的 , 甲、乙两个工厂每天各能加工多少个新产品?21. 如图 (1)、如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,说明理由.(2)、在四边形ABCD中,点E、F分别在BC、CD上,当AB=AD,∠B+∠D=180,∠EAF=∠BAD时,EF=BE+DF成立吗?请直接写出结论.22. 如图1,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx-6经过A(-3,0),B(2,0)两点.
(1)、如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,说明理由.(2)、在四边形ABCD中,点E、F分别在BC、CD上,当AB=AD,∠B+∠D=180,∠EAF=∠BAD时,EF=BE+DF成立吗?请直接写出结论.22. 如图1,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx-6经过A(-3,0),B(2,0)两点. (1)、求抛物线的解析式;(2)、如图2,点C是第三象限抛物线上的一个动点,过点C作x轴的平行线交抛物线于另一点D,连接BC,设点C的横坐标为t,∠BCD的正切值为m,当t<-时,求m与t的函数关系式(不要求写出自变量t的取值范围);(3)、如图3,在(2)的条件下,过点A作x轴的垂线l,点E在直线l上,连接AC,DE交于点F,当2∠CDF+∠CFD=90°,且AC=DE时,求m的值;请在射线CB上取点G,连接AG,EG,若△AEG为等腰三角形,直接写出符合条件的所有点G的坐标.
(1)、求抛物线的解析式;(2)、如图2,点C是第三象限抛物线上的一个动点,过点C作x轴的平行线交抛物线于另一点D,连接BC,设点C的横坐标为t,∠BCD的正切值为m,当t<-时,求m与t的函数关系式(不要求写出自变量t的取值范围);(3)、如图3,在(2)的条件下,过点A作x轴的垂线l,点E在直线l上,连接AC,DE交于点F,当2∠CDF+∠CFD=90°,且AC=DE时,求m的值;请在射线CB上取点G,连接AG,EG,若△AEG为等腰三角形,直接写出符合条件的所有点G的坐标.