广东省深圳市2022年九年级数学二模试题
试卷更新日期:2022-04-18 类型:中考模拟
一、单选题
-
1. 下面几何体的左视图为( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 据统计,全国共有346支医疗队,将近42600名医护工作者加入到支援湖北武汉的抗疫队伍,将42600用科学记数法表示为( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 不等式的解集是( )A、 B、 C、 D、5. 一副三角板如图所示摆放,若 ,则 的度数是( )
2. 据统计,全国共有346支医疗队,将近42600名医护工作者加入到支援湖北武汉的抗疫队伍,将42600用科学记数法表示为( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 不等式的解集是( )A、 B、 C、 D、5. 一副三角板如图所示摆放,若 ,则 的度数是( )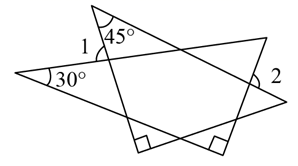 A、80° B、95° C、100° D、110°6. 九年级(3)班小王和小张两人练习跳绳,小王每分钟比小张少跳60个,小王跳120个所用的时间和小张跳180个所用的时间相等.设小王跳绳速度为x个每分钟,则列方程正确的是( )A、 B、 C、 D、7. 下列命题中,是真命题的是( )A、三角形的外心是三角形三个内角角平分线的交点 B、16的平方根是4 C、对角线相等的四边形各边中点连线所得四边形是矩形 D、五边形的内角和为540°8. 如图,小明利用一个锐角是30°的三角板测操场旗杆的高度,已知他与旗杆之间的水平距离BC为15m,AB为1.5m(即小明的眼睛与地面的距离),那么旗杆的高度是( )
A、80° B、95° C、100° D、110°6. 九年级(3)班小王和小张两人练习跳绳,小王每分钟比小张少跳60个,小王跳120个所用的时间和小张跳180个所用的时间相等.设小王跳绳速度为x个每分钟,则列方程正确的是( )A、 B、 C、 D、7. 下列命题中,是真命题的是( )A、三角形的外心是三角形三个内角角平分线的交点 B、16的平方根是4 C、对角线相等的四边形各边中点连线所得四边形是矩形 D、五边形的内角和为540°8. 如图,小明利用一个锐角是30°的三角板测操场旗杆的高度,已知他与旗杆之间的水平距离BC为15m,AB为1.5m(即小明的眼睛与地面的距离),那么旗杆的高度是( ) A、 B、 C、 D、9. 如图,抛物线y=ax2+bx+c和直线y=kx+b都经过点(﹣1,0),抛物线的对称轴为x=1,那么下列说法正确的是( )
A、 B、 C、 D、9. 如图,抛物线y=ax2+bx+c和直线y=kx+b都经过点(﹣1,0),抛物线的对称轴为x=1,那么下列说法正确的是( )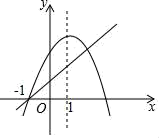 A、ac>0 B、b2﹣4ac<0 C、k=2a+c D、x=4是ax2+(b﹣k)x+c<b的解10. 如图,E为正方形ABCD边AB上一动点(不与A重合),AB=4,将△DAE绕着点A逆时针旋转90°得到△BAF,再将△DAE沿直线DE折叠得到△DME.下列结论:①连结AM,则AM∥FB;②连结FE,当F、E、M共线时,AE=4-4;③连结EF、EC、FC,若△FEC是等腰三角形,则AE=4-4;④连结EF,设FC、ED交于点O,若FE平分∠BFC,则O是FC的中点,且AE=2-2,其中正确的个数有( )个.
A、ac>0 B、b2﹣4ac<0 C、k=2a+c D、x=4是ax2+(b﹣k)x+c<b的解10. 如图,E为正方形ABCD边AB上一动点(不与A重合),AB=4,将△DAE绕着点A逆时针旋转90°得到△BAF,再将△DAE沿直线DE折叠得到△DME.下列结论:①连结AM,则AM∥FB;②连结FE,当F、E、M共线时,AE=4-4;③连结EF、EC、FC,若△FEC是等腰三角形,则AE=4-4;④连结EF,设FC、ED交于点O,若FE平分∠BFC,则O是FC的中点,且AE=2-2,其中正确的个数有( )个. A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
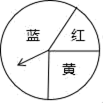
11. 因式分解: .12. 如图,一个游戏转盘中,红、黄、蓝三个扇形的圆心角度数分别为60°,90°,210°.让转盘自由转动,则指针停止后落在黄色区域的概率是 .
 13. 如图,△ABC中,∠ACB=90°,AC=BC=4,点P在以斜边AB为直径的半圆上,点M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长为 .
13. 如图,△ABC中,∠ACB=90°,AC=BC=4,点P在以斜边AB为直径的半圆上,点M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长为 .
三、解答题
-
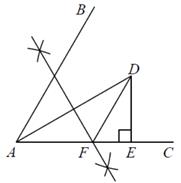
14. 如图,已知 , 是角平分线且 ,作 的垂直平分线交 于点F , 作 ,则 周长为 .
 15. 如图,在平面直角坐标系中,将直线y=-3x向上平移3个单位,与y轴、x轴分别交于点A、B,以线段AB为斜边在第一象限内作等腰直角三角形ABC.若反比例函数(x>0)的图象经过点C,则k的值为 .
15. 如图,在平面直角坐标系中,将直线y=-3x向上平移3个单位,与y轴、x轴分别交于点A、B,以线段AB为斜边在第一象限内作等腰直角三角形ABC.若反比例函数(x>0)的图象经过点C,则k的值为 .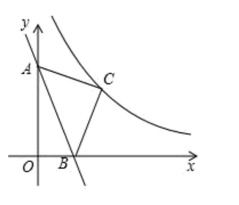 16. 计算: .17. 已知△ABC中,BC边的长为x,BC边上的高为y,△ABC的面积为3.(1)、写出y关于x的函数关系式;x的取值范围是 .(2)、列表,得
16. 计算: .17. 已知△ABC中,BC边的长为x,BC边上的高为y,△ABC的面积为3.(1)、写出y关于x的函数关系式;x的取值范围是 .(2)、列表,得x
…
1
2
3
4
…
y
…
▲
▲
▲
▲
…
在给出的坐标系中描点并连线;
 (3)、如果A(x1 , y1),B(x2 , y2)是图象上的两个点,且x1>x2>0,试判断y1 , y2的大小.18. 某校教务处为了解九年级学生“居家学习”的学习能力,随机抽取该年级部分学生,对他们的学习能力进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图(其中学习能力指数级别“1”级,代表学习能力很强;“2”级,代表学习能力较强;“3”级,代表学习能力一般;“4“级,代表学习能力较弱)请结合图中相关数据回答问题.
(3)、如果A(x1 , y1),B(x2 , y2)是图象上的两个点,且x1>x2>0,试判断y1 , y2的大小.18. 某校教务处为了解九年级学生“居家学习”的学习能力,随机抽取该年级部分学生,对他们的学习能力进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图(其中学习能力指数级别“1”级,代表学习能力很强;“2”级,代表学习能力较强;“3”级,代表学习能力一般;“4“级,代表学习能力较弱)请结合图中相关数据回答问题. (1)、本次抽查的学生人数 ▲ 人,并将条形统计图补充完整;(2)、本次抽查学生“居家学习”能力指数级别的众数为级,中位数为级.(3)、已知学习能力很强的学生中只有1名女生,现从中随机抽取两人写有关“居家学习”的报告,请用列表或画树状图的方法求所抽查的两位学生中恰好是一男一女的概率.19. 如图,在中, , 点O在上, , 点D在上,以点O为圆心,为半径作圆,交的延长线于点E,交于点F, .
(1)、本次抽查的学生人数 ▲ 人,并将条形统计图补充完整;(2)、本次抽查学生“居家学习”能力指数级别的众数为级,中位数为级.(3)、已知学习能力很强的学生中只有1名女生,现从中随机抽取两人写有关“居家学习”的报告,请用列表或画树状图的方法求所抽查的两位学生中恰好是一男一女的概率.19. 如图,在中, , 点O在上, , 点D在上,以点O为圆心,为半径作圆,交的延长线于点E,交于点F, . (1)、求证:为⊙O的切线;(2)、若⊙O的半径为3, , 求的长.20. 冰墩墩(BingDwenDwen),是2022年北京冬季奥运会的吉祥物.将熊猫形象与富有超能量的冰晶外壳相结合,头部外壳造型取自冰雪运动头盔,装饰彩色光环,整体形象酷似航天员.冬奥会来临之际,冰墩墩玩偶非常畅销.小冬在某网店选中A,B两款冰墩墩玩偶,决定从该网店进货并销售.两款玩偶的进货价和销售价如下表:
(1)、求证:为⊙O的切线;(2)、若⊙O的半径为3, , 求的长.20. 冰墩墩(BingDwenDwen),是2022年北京冬季奥运会的吉祥物.将熊猫形象与富有超能量的冰晶外壳相结合,头部外壳造型取自冰雪运动头盔,装饰彩色光环,整体形象酷似航天员.冬奥会来临之际,冰墩墩玩偶非常畅销.小冬在某网店选中A,B两款冰墩墩玩偶,决定从该网店进货并销售.两款玩偶的进货价和销售价如下表:A款玩偶
B款玩偶
进货价(元/个)
20
15
销售价(元/个)
28
20
(1)、第一次小冬550元购进了A,B两款玩偶共30个,求两款玩偶各购进多少个.(2)、第二次小冬进货时,网店规定A款玩偶进货数量不得超过B款玩偶进货数量的一半.小冬计划购进两款玩偶共30个,应如何设计进货方案才能获得最大利润,最大利润是多少?21.(1)、【问题情境】
如图1,在正方形ABCD中,E,F,G分别是BC,AB,CD上的点,FG⊥AE于点Q.求证:AE=FG.
(2)、【尝试应用】如图2,正方形网格中,点A,B,C,D为格点,AB交CD于点O.求tan∠AOC的值;
(3)、【拓展提升】如图3,点P是线段AB上的动点,分别以AP,BP为边在AB的同侧作正方形APCD与正方形PBEF,连接DE分别交线段BC,PC于点M,N.
①求∠DMC的度数;
②连接AC交DE于点H,直接写出的值.
22. 如图,对称轴为直线x=﹣1的抛物线y=a(x﹣h)2+k(a≠0)图象与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,其中点B的坐标为(2,0),点C的坐标为(0,4). (1)、求该抛物线的解析式:(2)、如图1,若点P为抛物线上第二象限内的一个动点,点M为线段CO上一动点,当△APC的面积最大时,求△APM周长最小值;(3)、如图2,将原抛物线绕点A旋转180°,得新抛物线y',在新抛物线)y'的对称轴上是否存在点Q使得△ACQ为等腰三角形?若存在,请直接写出点Q的坐标;若不存在,说明理由.
(1)、求该抛物线的解析式:(2)、如图1,若点P为抛物线上第二象限内的一个动点,点M为线段CO上一动点,当△APC的面积最大时,求△APM周长最小值;(3)、如图2,将原抛物线绕点A旋转180°,得新抛物线y',在新抛物线)y'的对称轴上是否存在点Q使得△ACQ为等腰三角形?若存在,请直接写出点Q的坐标;若不存在,说明理由.