广东省梅州市2022年中考数学模拟试题(一)
试卷更新日期:2022-04-18 类型:中考模拟
一、单选题
-
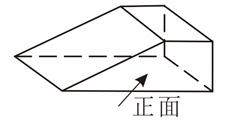
1. 在下列实数中,无理数是( )A、 B、 C、 D、2. 若 , 那么( )A、1 B、-1 C、-3 D、-53. 如图所示的几何体的俯视图是( )
 A、
A、 B、
B、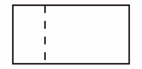 C、
C、 D、
D、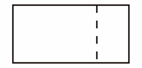 4. 按下图程序计算,若开始输入的值为x=5,则最后输出的结果是( )
4. 按下图程序计算,若开始输入的值为x=5,则最后输出的结果是( ) A、13 B、33 C、83 D、2085. 在△ABC中,∠C=90°,BC=2,sinA= ,则边AC的长是( )A、 B、3 C、 D、6. 某商品经过两次降价,售价由原来的每件25元降到每件16元,已知两次降价的百分率相同,则每次降价的百分率为( )A、 B、 C、 D、7. 下面四个手机应用图标中是轴对称图形的是( )
A、13 B、33 C、83 D、2085. 在△ABC中,∠C=90°,BC=2,sinA= ,则边AC的长是( )A、 B、3 C、 D、6. 某商品经过两次降价,售价由原来的每件25元降到每件16元,已知两次降价的百分率相同,则每次降价的百分率为( )A、 B、 C、 D、7. 下面四个手机应用图标中是轴对称图形的是( )
A、 B、
B、 C、
C、 D、
D、 8. 某中学七(1)班的6位同学在课间体育活动时进行一分钟跳绳比赛,成绩(单位:个)如下:122,146,134,146,152,121.这组数据的众数和中位数分别是( )A、152,134 B、146,146 C、146,140 D、152,1409. 在△ABC中,∠A=20°,∠B=4∠C,则∠C等于( )A、32° B、36° C、40° D、128°10. 二次函数的部分图象如图所示,图象经过点 , 对称轴为直线 , 下列结论:①;②;③若点、点、点在该函数图象上,则;④若方程的两根为和 , 且 , 则 , 其中正确的结论有( )
8. 某中学七(1)班的6位同学在课间体育活动时进行一分钟跳绳比赛,成绩(单位:个)如下:122,146,134,146,152,121.这组数据的众数和中位数分别是( )A、152,134 B、146,146 C、146,140 D、152,1409. 在△ABC中,∠A=20°,∠B=4∠C,则∠C等于( )A、32° B、36° C、40° D、128°10. 二次函数的部分图象如图所示,图象经过点 , 对称轴为直线 , 下列结论:①;②;③若点、点、点在该函数图象上,则;④若方程的两根为和 , 且 , 则 , 其中正确的结论有( ) A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
11. 用科学记数法表示的近似数精确到了 .12. 如图,四边形与四边形位似,其位似中心为点O,且 , 则 .
 13. 若分式 有意义,则 的取值范围是.14. 如图,在中,点、分别为边、上的点,连接 , 将沿翻折得到 , 使 . 若 , , 则的大小为 .
13. 若分式 有意义,则 的取值范围是.14. 如图,在中,点、分别为边、上的点,连接 , 将沿翻折得到 , 使 . 若 , , 则的大小为 . 15. 分解因式: .16. 如图,点M是函数y=x与y=的图象在第一象限内的交点,OM=8,则k的值为 .
15. 分解因式: .16. 如图,点M是函数y=x与y=的图象在第一象限内的交点,OM=8,则k的值为 . 17. 如图,菱形 中, , ,延长 至 ,使 ,以 为一边,在 的延长线上作菱形 ,连接 ,得到 ;再延长 至 ,使 ,以 为一边,在 的延长线上作菱形 ,连接 ,得到 ……按此规律,得到 ,记 的面积为 , 的面积为 …… 的面积为 ,则 .
17. 如图,菱形 中, , ,延长 至 ,使 ,以 为一边,在 的延长线上作菱形 ,连接 ,得到 ;再延长 至 ,使 ,以 为一边,在 的延长线上作菱形 ,连接 ,得到 ……按此规律,得到 ,记 的面积为 , 的面积为 …… 的面积为 ,则 .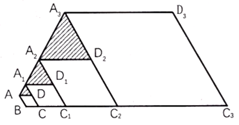
三、解答题
-
18.(1)、计算:(2)、先化简,再求值: , 其中 .19. 如图,四边形中, , , 连接 .
 (1)、尺规作图:过点作的垂线,垂足为(不要求写作法,保留作图痕迹);(2)、在(1)的条件下,已知四边形的面积为20, , 求的长.20. 教育部下发的《关于进一步加强中小学生睡眠管理工作的通知》要求,初中生每天睡眠时间应达到9h.某初中为了解学生每天的睡眠时间,随机调查了部分学生,将学生睡眠时间分为A , B , C , D四组(每名学生必须选择且只能选择一种情况):
(1)、尺规作图:过点作的垂线,垂足为(不要求写作法,保留作图痕迹);(2)、在(1)的条件下,已知四边形的面积为20, , 求的长.20. 教育部下发的《关于进一步加强中小学生睡眠管理工作的通知》要求,初中生每天睡眠时间应达到9h.某初中为了解学生每天的睡眠时间,随机调查了部分学生,将学生睡眠时间分为A , B , C , D四组(每名学生必须选择且只能选择一种情况):A组:睡眠时间<8h
B组:8h≤睡眠时间<9h
C组:9h≤睡眠时间<10h
D组:睡眠时间≥10h
如图1和图2是根据调查结果绘制的不完整的统计图,请根据图中提供的信息,解答下列问题:
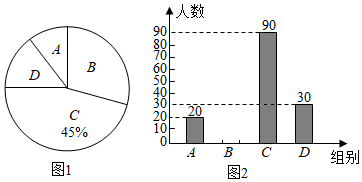 (1)、被调查的学生有人;(2)、通过计算补全条形统计图;(3)、请估计全校1200名学生中睡眠时间不足9h的人数.21. 某超市经销甲、乙两种品牌的洗衣液,进货时发现,甲品牌洗衣液每瓶的进价比乙品牌高6元,用1800元购进甲品牌洗衣液的数量是用1800元购进乙品牌洗衣液数量的 . 销售时,甲品牌洗衣液的售价为36元/瓶,乙品牌洗衣液的售价为28元/瓶.(1)、求两种品牌洗衣液的进价;(2)、若超市需要购进甲、乙两种品牌的洗衣液共120瓶,且购进两种洗衣液的总成本不超过3120元,超市应购进甲、乙两种品牌洗衣液各多少瓶,才能在两种洗衣液完全售出后所获利润最大?最大利润是多少元?22. 全国历史文化名城宜宾有许多名胜古迹,始建于明朝的白塔是其中之一.如图,为了测量白塔的高度AB,在C处测得塔顶A的仰角为45°,再向白塔方向前进15米到达D处,又测得塔顶A的仰角为60°,点B、D、C在同一水平线上,求白塔的高度AB.( ≈1.7,精确到1米)
(1)、被调查的学生有人;(2)、通过计算补全条形统计图;(3)、请估计全校1200名学生中睡眠时间不足9h的人数.21. 某超市经销甲、乙两种品牌的洗衣液,进货时发现,甲品牌洗衣液每瓶的进价比乙品牌高6元,用1800元购进甲品牌洗衣液的数量是用1800元购进乙品牌洗衣液数量的 . 销售时,甲品牌洗衣液的售价为36元/瓶,乙品牌洗衣液的售价为28元/瓶.(1)、求两种品牌洗衣液的进价;(2)、若超市需要购进甲、乙两种品牌的洗衣液共120瓶,且购进两种洗衣液的总成本不超过3120元,超市应购进甲、乙两种品牌洗衣液各多少瓶,才能在两种洗衣液完全售出后所获利润最大?最大利润是多少元?22. 全国历史文化名城宜宾有许多名胜古迹,始建于明朝的白塔是其中之一.如图,为了测量白塔的高度AB,在C处测得塔顶A的仰角为45°,再向白塔方向前进15米到达D处,又测得塔顶A的仰角为60°,点B、D、C在同一水平线上,求白塔的高度AB.( ≈1.7,精确到1米)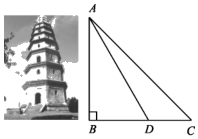 23. 如图,以△ABC的边BC为直径作⊙O,点A在⊙O上,点D在线段BC的延长线上,AD=AB,∠D=30°.
23. 如图,以△ABC的边BC为直径作⊙O,点A在⊙O上,点D在线段BC的延长线上,AD=AB,∠D=30°. (1)、求证:直线AD是⊙O的切线;(2)、过点O作OE∥AB交AC与点E,若直径BC=4,求OE的长.24. 如图1,在Rt△ABC中,∠ACB=90°,CA=CB,点D为AB边上一动点,连接CD,并将CD绕点C逆时针旋转90°得到CE,连接BE、DE,点F为DE中点,连接BF.
(1)、求证:直线AD是⊙O的切线;(2)、过点O作OE∥AB交AC与点E,若直径BC=4,求OE的长.24. 如图1,在Rt△ABC中,∠ACB=90°,CA=CB,点D为AB边上一动点,连接CD,并将CD绕点C逆时针旋转90°得到CE,连接BE、DE,点F为DE中点,连接BF. (1)、求证:△ACD△BCE;(2)、如图2所示,在点D的运动过程中,当时(n>1),分别延长AC、BF相交于G:
(1)、求证:△ACD△BCE;(2)、如图2所示,在点D的运动过程中,当时(n>1),分别延长AC、BF相交于G:①当时,求CG与AB的数量关系;
②当=n时(n>1),= ▲ .
(3)、当点D运动时,在线段CD上存在一点M,使得AM+BM+CM的值最小,若CM=2,则BE= .25. 如图,在平面直角坐标系中,抛物线的顶点坐标为 , 与轴交于点 , 与交于点 , . (1)、求二次函数的表达式;(2)、过点作平行于轴,交抛物线于点 , 点为抛物线上的一点(点在上方),作平行于轴交于点 , 当点在何位置时,四边形的面积最大?求出最大面积;(3)、若点在抛物线上,点在其对称轴上,以 , , , 为顶点的四边形是平行四边形,且为其一边,求点的坐标.
(1)、求二次函数的表达式;(2)、过点作平行于轴,交抛物线于点 , 点为抛物线上的一点(点在上方),作平行于轴交于点 , 当点在何位置时,四边形的面积最大?求出最大面积;(3)、若点在抛物线上,点在其对称轴上,以 , , , 为顶点的四边形是平行四边形,且为其一边,求点的坐标.