广东省广州市黄埔区2022年中考一模数学试题
试卷更新日期:2022-04-18 类型:中考模拟
一、单选题
-
1. 实数 , ,2,-3中,为负整数的是( )A、 B、 C、2 D、-32. 如图,数轴上有三个点A,B,C,若点A,B表示的数互为相反数,则图中点C对应的数是( )
 A、﹣2 B、0 C、1 D、43. 方程 的解为( )A、 B、 C、 D、4. 下列运算中,正确的是( )A、 B、 C、 D、5. 下列命题是真命题的是( )A、对角线相等的四边形是平行四边形 B、对角线互相平分且相等的四边形是矩形 C、对角线互相垂直的四边形是菱形 D、对角线互相垂直平分的四边形是正方形6. 在一个不透明的袋子里装有5个小球,每个球上都写有一个数字,分别是1,2,3,4,5,这些小球除数字不同外其它均相同.从中随机一次摸出两个小球,小球上的数字都是奇数的概率为( )A、 B、 C、 D、7. 如图,等边 的三个顶点都在 上, 是 的直径.若 ,则劣弧 的长是( )
A、﹣2 B、0 C、1 D、43. 方程 的解为( )A、 B、 C、 D、4. 下列运算中,正确的是( )A、 B、 C、 D、5. 下列命题是真命题的是( )A、对角线相等的四边形是平行四边形 B、对角线互相平分且相等的四边形是矩形 C、对角线互相垂直的四边形是菱形 D、对角线互相垂直平分的四边形是正方形6. 在一个不透明的袋子里装有5个小球,每个球上都写有一个数字,分别是1,2,3,4,5,这些小球除数字不同外其它均相同.从中随机一次摸出两个小球,小球上的数字都是奇数的概率为( )A、 B、 C、 D、7. 如图,等边 的三个顶点都在 上, 是 的直径.若 ,则劣弧 的长是( )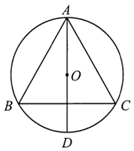 A、 B、 C、 D、8. 已知抛物线 上的部分点的横坐标x与纵坐标y的对应值如表:
A、 B、 C、 D、8. 已知抛物线 上的部分点的横坐标x与纵坐标y的对应值如表:x
…
-1
0
1
2
3
…
y
…
3
0
-1
m
3
…
以下结论正确的是( )
A、抛物线 的开口向下 B、当 时,y随x增大而增大 C、方程 的根为0和2 D、当 时,x的取值范围是9. 如图,在△ABC中,点O是角平分线AD、BE的交点,若AB=AC=10,BC=12,则tan∠OBD的值是( ) A、 B、2 C、 D、10. 如图,在平面直角坐标系中,矩形ABCD的对角线AC的中点与坐标原点重合,点E是x轴上一点,连接AE.若AD平分 ,反比例函数 的图象经过AE上的两点A,F,且 , 的面积为18,则k的值为( )
A、 B、2 C、 D、10. 如图,在平面直角坐标系中,矩形ABCD的对角线AC的中点与坐标原点重合,点E是x轴上一点,连接AE.若AD平分 ,反比例函数 的图象经过AE上的两点A,F,且 , 的面积为18,则k的值为( )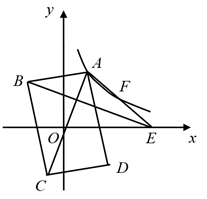 A、6 B、12 C、18 D、24
A、6 B、12 C、18 D、24二、填空题
-
11. 若 在实数范围内有意义,则x的取值范围为 .12. 一元二次方程 的根是 .13. 若点 、 、 都在反比例函数 (k为常数)的图象上,则 、 、 的大小关系为 .14. 如图,将分别含有 、 角的一副三角板重叠,使直角顶点重合,若两直角重叠形成的角为 ,则图中角 的度数为.
 15. 如图,AB为半圆O的直径,M,C是半圆上的三等分点,AB=8,BD与半圆O相切于点B.点P为上一动点(不与点A,M重合),直线PC交BD于点D,BE⊥OC于点E,延长BE交PC于点F,则下列结论正确的是 . (写出所有正确结论的序号)
15. 如图,AB为半圆O的直径,M,C是半圆上的三等分点,AB=8,BD与半圆O相切于点B.点P为上一动点(不与点A,M重合),直线PC交BD于点D,BE⊥OC于点E,延长BE交PC于点F,则下列结论正确的是 . (写出所有正确结论的序号)①PB=PD;②的长为;③∠DBE=45°;④△BCF∽△PFB;⑤为定值.

三、解答题
-
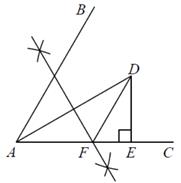
16. 如图,已知 , 是角平分线且 ,作 的垂直平分线交 于点F , 作 ,则 周长为 .
 17. 解方程组:18. 如图,AC是∠BAE的平分线,点D是线段AC上的一点,∠C=∠E,AB=AD.求证:BC=DE.
17. 解方程组:18. 如图,AC是∠BAE的平分线,点D是线段AC上的一点,∠C=∠E,AB=AD.求证:BC=DE.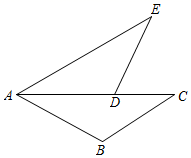 19. 已知 , 且 , 求的值.20. 中华文化源远流长,文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查,根据调查结果绘制成如下尚不完整的统计图.
19. 已知 , 且 , 求的值.20. 中华文化源远流长,文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查,根据调查结果绘制成如下尚不完整的统计图.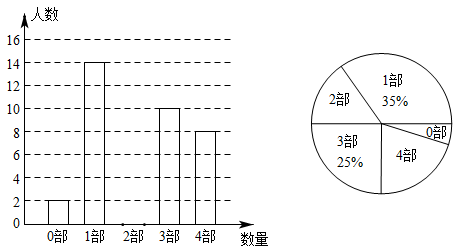
请根据以上信息,解决下列问题:
(1)、本次调查所得数据的众数是部,中位数是部;(2)、扇形统计图中“4部”所在扇形的圆心角为度;(3)、请将条形统计图补充完整;(4)、没有读过四大古典名著的两名学生准备从中各自随机选择一部来阅读,请用列表或画树状图的方法求他们恰好选中同一名著的概率.21. 为保障新冠病毒疫苗接种需求,某生物科技公司开启“加速”模式,生产效率比原先提高了20%,现在生产240万剂疫苗所用的时间比原先生产220万剂疫苗所用的时间少0.5天,问原先每天生产多少万剂疫苗?22. 如图,已知△ABC是锐角三角形(AC<AB). (1)、请在图1中用无刻度的直尺和圆规作图:作直线l,使l上的各点到B、C两点的距离相等;设直线l与AB、BC分别交于点M、N,作一个圆,使得圆心O在线段MN上,且与边AB、BC相切;(不写作法,保留作图痕迹)(2)、在(1)的条件下,若 , BC=2,求⊙O的半径.23. 在平面直角坐标系中,直线y=kx+4(k≠0)交x轴于点A(8,0),交y轴于点B,
(1)、请在图1中用无刻度的直尺和圆规作图:作直线l,使l上的各点到B、C两点的距离相等;设直线l与AB、BC分别交于点M、N,作一个圆,使得圆心O在线段MN上,且与边AB、BC相切;(不写作法,保留作图痕迹)(2)、在(1)的条件下,若 , BC=2,求⊙O的半径.23. 在平面直角坐标系中,直线y=kx+4(k≠0)交x轴于点A(8,0),交y轴于点B, (1)、k的值是;(2)、点C是直线AB上的一个动点,点D和点E分别在x轴和y轴上.
(1)、k的值是;(2)、点C是直线AB上的一个动点,点D和点E分别在x轴和y轴上.①如图,点E为线段OB的中点,且四边形OCED是平行四边形时,求▱OCED的周长;
②当CE平行于x轴,CD平行于y轴时,连接DE,若△CDE的面积为 , 请直接写出点C的坐标.
24. 已知抛物线y=ax2+bx+3经过点和点 , 与y轴交于点C,P为第二象限内抛物线上一点. (1)、求抛物线的解析式,并写出顶点坐标;(2)、如图,连接PB,PO,PC,BC,OP交BC于点D,当S△CPD:S△BPD=1:2时,求出点D的坐标.25. 在△ABC和△ADE中,AC=BC,AE=DE,且AE<AC,∠ACB=∠AED=90°,将△ADE绕点A顺时针方向旋转,把点E在AC边上时△ADE的位置作为起始位置(此时点B和点D位于AC的两侧),设旋转角为α,连接BD,点P是线段BD的中点,连接PC,PE.
(1)、求抛物线的解析式,并写出顶点坐标;(2)、如图,连接PB,PO,PC,BC,OP交BC于点D,当S△CPD:S△BPD=1:2时,求出点D的坐标.25. 在△ABC和△ADE中,AC=BC,AE=DE,且AE<AC,∠ACB=∠AED=90°,将△ADE绕点A顺时针方向旋转,把点E在AC边上时△ADE的位置作为起始位置(此时点B和点D位于AC的两侧),设旋转角为α,连接BD,点P是线段BD的中点,连接PC,PE. (1)、如图1,当△ADE在起始位置时,猜想:PC与PE的数量关系和位置关系,并说明理由;(2)、如图2,当时,点D落在AB边上,请判断PC与PE的数量关系和位置关系,并证明你的结论;(3)、当α=150°时,若BC=3,DE=1,请直接写出PC2的值.
(1)、如图1,当△ADE在起始位置时,猜想:PC与PE的数量关系和位置关系,并说明理由;(2)、如图2,当时,点D落在AB边上,请判断PC与PE的数量关系和位置关系,并证明你的结论;(3)、当α=150°时,若BC=3,DE=1,请直接写出PC2的值.