广东省佛山市南海区2022年中考一模数学试题
试卷更新日期:2022-04-18 类型:中考模拟
一、单选题
-
1. 在下列各数中,比小的数是( )A、1 B、0 C、 D、-22. 可燃冰,学名叫“天然气水合物”,是一种高效清洁、储量巨大的新能源.据报道,仅我国可燃冰预测远景资源量就超过了1000亿吨油当量.将1000亿用科学记数法可表示为( )A、1×103 B、100×108 C、1×1011 D、1×10143. 一个不透明的布袋里装有7个只有颜色不同的球,其中4个白球,2个红球,1个黄球。从布袋里任意摸出1个球,是红球的概率为( )A、 B、 C、 D、4. 在 中, , 平分 ,交 于点D, ,垂足为点E,若 ,则 的长为( )
 A、3 B、 C、2 D、65. 下列运算结果正确的是( )A、 B、 C、 D、6. 一副三角板如图就置,两三角板的斜边互相平行,每个三角板的直角顶点都在另一个三角板的斜边上,图中 的度数为( )
A、3 B、 C、2 D、65. 下列运算结果正确的是( )A、 B、 C、 D、6. 一副三角板如图就置,两三角板的斜边互相平行,每个三角板的直角顶点都在另一个三角板的斜边上,图中 的度数为( )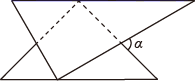 A、45° B、60° C、75° D、85°7. 将抛物线 向左平移2个单位,得到抛物线的解析式是( )A、 B、 C、 D、8. 不等式组的解集为( )A、 B、 C、 D、9. 如图,四边形 是平行四边形,点 为 的中点,延长 至点 ,使 ,连接 、 、 ,则在 中 ( )
A、45° B、60° C、75° D、85°7. 将抛物线 向左平移2个单位,得到抛物线的解析式是( )A、 B、 C、 D、8. 不等式组的解集为( )A、 B、 C、 D、9. 如图,四边形 是平行四边形,点 为 的中点,延长 至点 ,使 ,连接 、 、 ,则在 中 ( ) A、 B、 C、 D、10. 如图,菱形ABCD的边长为2,∠A=60°,点P和点Q分别从点B和点C出发,沿射线BC向右运动,且速度相同,过点Q作QH⊥BD,垂足为H,连接PH,设点P运动的距离为x(0<x≤2),△BPH的面积为S,则能反映S与x之间的函数关系的图象大致为( )
A、 B、 C、 D、10. 如图,菱形ABCD的边长为2,∠A=60°,点P和点Q分别从点B和点C出发,沿射线BC向右运动,且速度相同,过点Q作QH⊥BD,垂足为H,连接PH,设点P运动的距离为x(0<x≤2),△BPH的面积为S,则能反映S与x之间的函数关系的图象大致为( ) A、
A、 B、
B、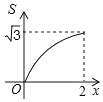 C、
C、 D、
D、
二、填空题
-
11. 分解因式:2 =.12. 若代数式 有意义,则实数x的取值范围是.13. 某个函数具有性质:当 >0时, 随 的增大而增大,这个函数的表达式可以是(只要写出一个正确的答案即可)14. 若 , 则关于x的方程解的取值范围为 .15. 如图,菱形 和菱形 的边长分别为 和 , ,则图中阴影部分的面积是 .
 16. 如图是一张矩形纸片ABCD,点M是对角线AC的中点,点E在BC边上,把沿直线DE折叠,使点C落在对角线AC上的点F处,连接DF,EF.若 , 则 .
16. 如图是一张矩形纸片ABCD,点M是对角线AC的中点,点E在BC边上,把沿直线DE折叠,使点C落在对角线AC上的点F处,连接DF,EF.若 , 则 . 17. 在平面直角坐标系中,已知点 . 若在x轴正半轴上有一点C.使 , 则点C的横坐标是 .
17. 在平面直角坐标系中,已知点 . 若在x轴正半轴上有一点C.使 , 则点C的横坐标是 .三、解答题
-
18. 计算:19. 先化简,再求值:( ﹣ )÷ ,其中a= .20. 随着社会的发展,私家车变得越来越普及,使用节能低油耗汽车,对环保有着非常积极的意义,某市有关部门对本市的某一型号的若干辆汽车,进行了一项油耗抽样实验:即在同一条件下,被抽样的该型号汽车,在油耗1L的情况下,所行驶的路程(单位:km)进行统计分析,结果如图所示:

(注:记A为12~12.5,B为12.5~13,C为13~13.5,D为13.5~14,E为14~14.5)
请依据统计结果回答以下问题:
(1)、试求进行该试验的车辆数;(2)、请补全频数分布直方图;(3)、若该市有这种型号的汽车约900辆(不考虑其他因素),请利用上述统计数据初步预测,该市约有多少辆该型号的汽车,在耗油1L的情况下可以行驶13km以上?21. 在“母亲节”前期,某花店购进康乃馨和玫瑰两种鲜花,销售过程中发现康乃馨比玫瑰销售量大,店主决定将玫瑰每枝降价1元促销,降价后30元可购买玫瑰的数量是原来购买玫瑰数量的1.5倍.(1)、求降价后每枝玫瑰的售价是多少元?(2)、根据销售情况,店主用不多于900元的资金再次购进两种鲜花共500枝,康乃馨进价为2元/枝,玫瑰进价为1.5元/枝,问至少购进玫瑰多少枝?22. 如图,AB为⊙O的直径,C为⊙O上一点,AD与过点C的切线互相垂直,垂足为点D,AD交⊙O于点E,连接CE,CB.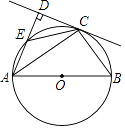 (1)、求证:CE=CB;(2)、若AC=2 ,CE= ,求AE的长.23. 如图,过C点的直线y=﹣ x﹣2与x轴,y轴分别交于点A,B两点,且BC=AB,过点C作CH⊥x轴,垂足为点H,交反比例函数y= (x>0)的图象于点D,连接OD,△ODH的面积为6
(1)、求证:CE=CB;(2)、若AC=2 ,CE= ,求AE的长.23. 如图,过C点的直线y=﹣ x﹣2与x轴,y轴分别交于点A,B两点,且BC=AB,过点C作CH⊥x轴,垂足为点H,交反比例函数y= (x>0)的图象于点D,连接OD,△ODH的面积为6 (1)、求k值和点D的坐标;(2)、如图,连接BD,OC,点E在直线y=﹣ x﹣2上,且位于第二象限内,若△BDE的面积是△OCD面积的2倍,求点E的坐标.24. 如图,在正方形ABCD中,点E、G分别是边AD、BC的中点,AF=AB
(1)、求k值和点D的坐标;(2)、如图,连接BD,OC,点E在直线y=﹣ x﹣2上,且位于第二象限内,若△BDE的面积是△OCD面积的2倍,求点E的坐标.24. 如图,在正方形ABCD中,点E、G分别是边AD、BC的中点,AF=AB (1)、求证:EF⊥AG;(2)、若点F、G分别在射线AB、BC上同时向右、向上运动,点G运动速度是点F运动速度的2倍,EF⊥AG是否成立(只写结果,不需说明理由)?(3)、正方形ABCD的边长为4,P是正方形ABCD内一点,当 , 求△PAB周长的最小值.25. 如图,二次函数 的图象过原点,与 轴的另一个交点为
(1)、求证:EF⊥AG;(2)、若点F、G分别在射线AB、BC上同时向右、向上运动,点G运动速度是点F运动速度的2倍,EF⊥AG是否成立(只写结果,不需说明理由)?(3)、正方形ABCD的边长为4,P是正方形ABCD内一点,当 , 求△PAB周长的最小值.25. 如图,二次函数 的图象过原点,与 轴的另一个交点为 (1)、求该二次函数的解析式;(2)、在 轴上方作 轴的平行线 ,交二次函数图象于 、 两点,过 、 两点分别作 轴的垂线,垂足分别为点 、点 .矩形 为正方形,求 的值;(3)、在(2)的条件下,动点 从点 出发沿射线 以每秒1个单位长度匀速运动,同时动点 以相同的速度从点 出发沿线段 匀速运动,到达点 时立即原速返回,当动点 返回到点 时, 、 两点同时停止运动,设运动时间为 秒( ).过点 向 轴作垂线,交抛物线于点 ,交直线 于点 ,当以 、 、 、 四点为顶点构成的四边形为平行四边形时,请求出 的值.
(1)、求该二次函数的解析式;(2)、在 轴上方作 轴的平行线 ,交二次函数图象于 、 两点,过 、 两点分别作 轴的垂线,垂足分别为点 、点 .矩形 为正方形,求 的值;(3)、在(2)的条件下,动点 从点 出发沿射线 以每秒1个单位长度匀速运动,同时动点 以相同的速度从点 出发沿线段 匀速运动,到达点 时立即原速返回,当动点 返回到点 时, 、 两点同时停止运动,设运动时间为 秒( ).过点 向 轴作垂线,交抛物线于点 ,交直线 于点 ,当以 、 、 、 四点为顶点构成的四边形为平行四边形时,请求出 的值.