广东省佛山市南海区里水镇2022年中考模拟数学试题
试卷更新日期:2022-04-18 类型:中考模拟
一、单选题
-
1. -3的倒数是( )A、 B、 C、 D、-32. 下列图形中,是中心对称图形,但不是轴对称图形的是( )A、
 B、
B、 C、
C、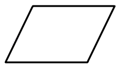 D、
D、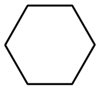 3. 一组数据5,3,3,2,5,7的中位数是( )A、2 B、2.5 C、3 D、44. 据专家预测,到2022年冬残奥会结束时,冬奥会场馆预计共消耗绿电4亿度,预计可减少标煤燃烧12.8万吨,减排二氧化碳32万吨,将“32万”用科学记数法表示为( )A、32×104 B、3.2×105 C、3.2×104 D、0.32×1065. 正多边形的一个内角为135°,则该多边形的边数为( )A、5 B、6 C、7 D、86. 已知a2﹣b2=15,a﹣b=3,则a+b的值是( )A、5 B、7 C、﹣5 D、﹣77. 如图,在等腰中, , , BD是的角平分线,则的度数等于( )
3. 一组数据5,3,3,2,5,7的中位数是( )A、2 B、2.5 C、3 D、44. 据专家预测,到2022年冬残奥会结束时,冬奥会场馆预计共消耗绿电4亿度,预计可减少标煤燃烧12.8万吨,减排二氧化碳32万吨,将“32万”用科学记数法表示为( )A、32×104 B、3.2×105 C、3.2×104 D、0.32×1065. 正多边形的一个内角为135°,则该多边形的边数为( )A、5 B、6 C、7 D、86. 已知a2﹣b2=15,a﹣b=3,则a+b的值是( )A、5 B、7 C、﹣5 D、﹣77. 如图,在等腰中, , , BD是的角平分线,则的度数等于( ) A、 B、 C、 D、8. 若x=5是方程﹣6x+k=0的一个根,则此方程的另一个根是( )A、1 B、2 C、3 D、49. 如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE.若AD=1,AB=2,则DE:AC的值为( )
A、 B、 C、 D、8. 若x=5是方程﹣6x+k=0的一个根,则此方程的另一个根是( )A、1 B、2 C、3 D、49. 如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE.若AD=1,AB=2,则DE:AC的值为( ) A、 B、 C、 D、10. 如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点G坐标为(1,k),且与x轴的一个交点在点(2,0)和(3,0)之间(不含两端点).则下列结论:
A、 B、 C、 D、10. 如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点G坐标为(1,k),且与x轴的一个交点在点(2,0)和(3,0)之间(不含两端点).则下列结论:①abc<0;②a﹣b+c>0;③3a+b<0;4a﹣2b+c>0;④一元二次方程ax2+bx+c=k+1没有实数根.其中正确结论的个数是( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 不等式组的解集是 .12. 分解因式a2+4ab+4b2﹣1= .13. 已知|x+2y|+(x﹣4)2=0,则xy= .14. 将半径为3m的半圆形铁皮围成一个圆锥形烟囱帽,则该圆锥的底面圆的半径为 m.15. 若关于x的方程无解,则a= .16. 如图,四边形ABCD是边长为5的正方形,∠CEB和∠CFD都是直角且点C,E,F三点共线,BE=2,则阴影部分的面积是 .
 17. 如图,在平面直角坐标系中,直线l:y=x﹣1与x轴交于点A1 , 以OA1为一边作正方形OA1B1C1 , 使得点C1在y轴正半轴上,延长C1B1交直线l于点A2 , 按同样方法依次作正方形C1A2B2C2、正方形C2A3B3C3…、正方形Cn-1AnBnCn , 使得点A1、A2、A3、…An均在直线l上,点C1、C2、C3、…Cn在y轴正半轴上,则点B2022的横坐标是 .
17. 如图,在平面直角坐标系中,直线l:y=x﹣1与x轴交于点A1 , 以OA1为一边作正方形OA1B1C1 , 使得点C1在y轴正半轴上,延长C1B1交直线l于点A2 , 按同样方法依次作正方形C1A2B2C2、正方形C2A3B3C3…、正方形Cn-1AnBnCn , 使得点A1、A2、A3、…An均在直线l上,点C1、C2、C3、…Cn在y轴正半轴上,则点B2022的横坐标是 .
三、解答题
-
18. 先化简,再求值: , 其中x=π0+1.19. 如图,△ABC中,AB=AC=4.
 (1)、请用尺规作图法,作AB边上的中线CD(要求:保留画图痕迹,不写作法);(2)、在所作的图形中,若CD=CB,求BC的长.20. 为提高教育质量,落实立德树人的根本任务,中共中央办公厅、国务院办公厅颁布了“双减”政策.为了调查学生对“双减”政策的了解程度,某学校数学兴趣小组通过网上调查的方式在本校学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查结果,绘制了如图的统计图,结合统计图,回答下列问题:
(1)、请用尺规作图法,作AB边上的中线CD(要求:保留画图痕迹,不写作法);(2)、在所作的图形中,若CD=CB,求BC的长.20. 为提高教育质量,落实立德树人的根本任务,中共中央办公厅、国务院办公厅颁布了“双减”政策.为了调查学生对“双减”政策的了解程度,某学校数学兴趣小组通过网上调查的方式在本校学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查结果,绘制了如图的统计图,结合统计图,回答下列问题: (1)、若该校有学生2000人,请根据调查结果估计这些学生中“比较了解”“双减”政策的人数约为多少?(2)、根据调查结果,学校准备开展关于“双减”政策宣传工作,要从某班“非常了解”的小明和小刚中选一个人参加,现设计了如下游戏来确定,具体规则是:在一个不透明的袋中装有2个红球和2个白球,它们除了颜色外无其他差别,从中随机摸出两个球,若摸出的两个球颜色相同,则小明去;否则小刚去.请用树状图或列表法说明这个游戏规则是否公平.21. 已知:如图,△ABC内接于圆O,且AB过圆心O,D是弧BC上的一点,OD⊥BC,垂足为H,连接AD、CD,AD与BC交于点P.
(1)、若该校有学生2000人,请根据调查结果估计这些学生中“比较了解”“双减”政策的人数约为多少?(2)、根据调查结果,学校准备开展关于“双减”政策宣传工作,要从某班“非常了解”的小明和小刚中选一个人参加,现设计了如下游戏来确定,具体规则是:在一个不透明的袋中装有2个红球和2个白球,它们除了颜色外无其他差别,从中随机摸出两个球,若摸出的两个球颜色相同,则小明去;否则小刚去.请用树状图或列表法说明这个游戏规则是否公平.21. 已知:如图,△ABC内接于圆O,且AB过圆心O,D是弧BC上的一点,OD⊥BC,垂足为H,连接AD、CD,AD与BC交于点P. (1)、求证:∠ACD=∠APB.(2)、若AC=6,AB=10,求AD的长.22. 面对世界百年未有之大变局和中华民族伟大复兴战略全局,党中央提出构建“国内国际双循环”新发展格局具有重大战略.某物流公司承接A、B两种出口货物的运输业务,已知3月份A货物运费单价为70元/吨,B货物运费单价为40元/吨,共收取运费180000元;4月份由于油价下调,运费单价下降为:A货物50元/吨,B货物30元/吨;该物流公司4月承接的两种货物的数量与3月份相同,4月份共收取运费130000元.(1)、该物流公司3月份运输两种货物各多少吨?(2)、该物流公司预计5月份运输这两种货物共3600吨,且A货物的数量不大于B货物的2倍,在运费单价与4月份相同的情况下,该物流公司5月份最多将收到多少运费?23. 我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为“勾股四边形”,这两条相邻的边称为这个四边形的勾股边.如图在四边形ABCD中,∠B=60°,∠D=30°,AB=BC.
(1)、求证:∠ACD=∠APB.(2)、若AC=6,AB=10,求AD的长.22. 面对世界百年未有之大变局和中华民族伟大复兴战略全局,党中央提出构建“国内国际双循环”新发展格局具有重大战略.某物流公司承接A、B两种出口货物的运输业务,已知3月份A货物运费单价为70元/吨,B货物运费单价为40元/吨,共收取运费180000元;4月份由于油价下调,运费单价下降为:A货物50元/吨,B货物30元/吨;该物流公司4月承接的两种货物的数量与3月份相同,4月份共收取运费130000元.(1)、该物流公司3月份运输两种货物各多少吨?(2)、该物流公司预计5月份运输这两种货物共3600吨,且A货物的数量不大于B货物的2倍,在运费单价与4月份相同的情况下,该物流公司5月份最多将收到多少运费?23. 我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为“勾股四边形”,这两条相邻的边称为这个四边形的勾股边.如图在四边形ABCD中,∠B=60°,∠D=30°,AB=BC. (1)、求∠A+∠C的度数;(2)、判断四边形ABCD是否“勾股四边形”,并说明理由.(3)、若AB=1,直接写出对角线BD长度的最大值.24. 如图,在△ABC中,点D、E、F分别在边BC、AB、CA上,且DE∥CA,DF∥AB.
(1)、求∠A+∠C的度数;(2)、判断四边形ABCD是否“勾股四边形”,并说明理由.(3)、若AB=1,直接写出对角线BD长度的最大值.24. 如图,在△ABC中,点D、E、F分别在边BC、AB、CA上,且DE∥CA,DF∥AB. (1)、若点D是边BC的中点,且BE=CF,求证:DE=DF;(2)、若AD⊥BC于D,且BD=CD,求证:四边形AEDF是菱形;(3)、若AE=AF=1,求的值.25. 抛物线y=ax2+4x+c交x轴于A、B两点,交y轴于点C,其顶点为M,且经过点B、C的直线解析式为y=﹣x+5.(1)、求抛物线的解析式.(2)、点D为抛物线对称轴上一点,点E为抛物线上一点,且以B、C、D、E为顶点的四边形为平行四边形,求点E的坐标.(3)、直线y=kx﹣2k+4(k>0)与抛物线交于点P、Q,若△MPQ的面积等于15,求k的值.
(1)、若点D是边BC的中点,且BE=CF,求证:DE=DF;(2)、若AD⊥BC于D,且BD=CD,求证:四边形AEDF是菱形;(3)、若AE=AF=1,求的值.25. 抛物线y=ax2+4x+c交x轴于A、B两点,交y轴于点C,其顶点为M,且经过点B、C的直线解析式为y=﹣x+5.(1)、求抛物线的解析式.(2)、点D为抛物线对称轴上一点,点E为抛物线上一点,且以B、C、D、E为顶点的四边形为平行四边形,求点E的坐标.(3)、直线y=kx﹣2k+4(k>0)与抛物线交于点P、Q,若△MPQ的面积等于15,求k的值.