安徽省全椒县2022年九年级下学期中考一模数学试题
试卷更新日期:2022-04-18 类型:中考模拟
一、单选题
-
1. 在5,0、-3、-5四个数中最小的数是( )A、5 B、0 C、-3 D、-52. 2022年1月4日上午备受瞩目的安徽G3铜陵长江公铁大桥正式动工兴建,新的一年开建的这座大桥总投资87.8亿元,其中87.8亿用科学记数法表示为( )A、 B、 C、 D、3. 如图是某一物体的三视图,则此三视图对应的物体是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列计算正确的是( )A、 B、 C、 D、5. 已知 , 则的值为( )A、 B、-3 C、 D、36. 刘老师每天从家去学校上班行走的路程为1200米,某天他从家去学校上班时以每分钟40米的速度行走了前半程,为了不迟到他加快了速度,以每分钟50米的速度行走完了剩下的路程,那么刘老师距离学校的路程(米)与他行走的时间(分)()之间的函数关系为( )A、 B、 C、 D、7. 若、、、是正整数,且 , , 下列结论正确的是( )A、 B、 C、 D、8. 如图,在矩形中, , , 以点为圆心,长为半径画弧,交边于点 , 则四边形的周长为( )
4. 下列计算正确的是( )A、 B、 C、 D、5. 已知 , 则的值为( )A、 B、-3 C、 D、36. 刘老师每天从家去学校上班行走的路程为1200米,某天他从家去学校上班时以每分钟40米的速度行走了前半程,为了不迟到他加快了速度,以每分钟50米的速度行走完了剩下的路程,那么刘老师距离学校的路程(米)与他行走的时间(分)()之间的函数关系为( )A、 B、 C、 D、7. 若、、、是正整数,且 , , 下列结论正确的是( )A、 B、 C、 D、8. 如图,在矩形中, , , 以点为圆心,长为半径画弧,交边于点 , 则四边形的周长为( ) A、79 B、86 C、82 D、929. 如图是建平同学收集到的四张“新基建”图标卡片,这四张卡片除正面的图标内容外,其余完全相同,将卡片背面朝上,洗匀放好,从中随机抽取一张(不放回),再从中随机抽取一张,则抽到的两张卡片恰好是“5G基站建设”和“大数据中心”的概率是( )
A、79 B、86 C、82 D、929. 如图是建平同学收集到的四张“新基建”图标卡片,这四张卡片除正面的图标内容外,其余完全相同,将卡片背面朝上,洗匀放好,从中随机抽取一张(不放回),再从中随机抽取一张,则抽到的两张卡片恰好是“5G基站建设”和“大数据中心”的概率是( ) A、 B、 C、 D、10. 正方形的边长为8,点、分别在边、上,将正方形沿折叠,使点落在处,点落在处,交于 . 下列结论不正确的是( )
A、 B、 C、 D、10. 正方形的边长为8,点、分别在边、上,将正方形沿折叠,使点落在处,点落在处,交于 . 下列结论不正确的是( ) A、当为中点时,则 B、当时,则 C、连接 , 则 D、当(点不与、重合)在上移动时,周长随着位置变化而变化
A、当为中点时,则 B、当时,则 C、连接 , 则 D、当(点不与、重合)在上移动时,周长随着位置变化而变化二、填空题
-
11. 计算: .12. 大自然是美的设计师,即使是一片小小的树叶,也蕴含着“美学”,如图, , 这个比值介于整数和之间,则的值是 .
 13. 如图,内接于 . 若 , , , 则的长是 .
13. 如图,内接于 . 若 , , , 则的长是 . 14. 如图,是等腰直角三角形, , 边上高为3.动点从点开始出发,以每秒3个单位长度的速度在射线上运动.连接 , 以为直角边向右作等腰 , 使 , 连接 , 设点的运动时间为秒.
14. 如图,是等腰直角三角形, , 边上高为3.动点从点开始出发,以每秒3个单位长度的速度在射线上运动.连接 , 以为直角边向右作等腰 , 使 , 连接 , 设点的运动时间为秒. (1)、长度为;(2)、当 , 且时,则的值为 .
(1)、长度为;(2)、当 , 且时,则的值为 .三、解答题
-
15. 解不等式: .16. 如图,在平面坐标内,三个顶点的坐标分别为 , , . (正方形网格中,每个小正方形的边长是1个单位长度)
 (1)、先将向下平移5个单位长度,再向左平移3个单位长度得到 , 请画出;(2)、把绕点顺时针方向旋转后得到 , 请画出并直接写出点的坐标.17. 为了丰富学生社会实践活动,学校组织学生到红色文化基地和人工智能科技馆参观学习.如图,学校在点处,位于学校的东北方向,位于学校南偏东方向,在的南偏西方向的处.求学校和红色文化基地之间的距离.
(1)、先将向下平移5个单位长度,再向左平移3个单位长度得到 , 请画出;(2)、把绕点顺时针方向旋转后得到 , 请画出并直接写出点的坐标.17. 为了丰富学生社会实践活动,学校组织学生到红色文化基地和人工智能科技馆参观学习.如图,学校在点处,位于学校的东北方向,位于学校南偏东方向,在的南偏西方向的处.求学校和红色文化基地之间的距离. 18. 观察下列等式:
18. 观察下列等式:第1个等式:;第2个等式:;
第3个等式:;第4个等式: .
…
请解答下列问题:
(1)、按以上规律列出第5个等式:;(2)、用含有的代数式表示第个等式:;(为正整数)(3)、试比较代数式的值与的大小关系.19. 如图,一次函数的图象交反比例函数的图象于点和点 . (1)、求 , 的值;(2)、根据图象,写出一次函数的值不小于反比例函数的值时取值范围.20. 如图,中两条互相垂直的弦 , 交于点 .
(1)、求 , 的值;(2)、根据图象,写出一次函数的值不小于反比例函数的值时取值范围.20. 如图,中两条互相垂直的弦 , 交于点 .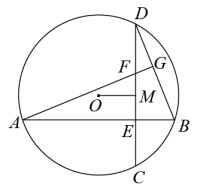 (1)、于点 , , 的半径长为 , 求的长;(2)、点在上,且交于点 , 求证: .21. 2021年12月4日是第八个国家宪法日,11月29日至12月5日是第四个“宪法宣传周”,合肥某校主办了以“学习法理,弘扬法治”为主题的大赛,全校10000名学生都参加了此次大赛,赛后发现所有参赛学生的成绩均不低于50分且没有满分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩取整数,总分100分)进行分组,分别为组:;组:;组:;组:;组: , 并绘制了频数分布直方图.
(1)、于点 , , 的半径长为 , 求的长;(2)、点在上,且交于点 , 求证: .21. 2021年12月4日是第八个国家宪法日,11月29日至12月5日是第四个“宪法宣传周”,合肥某校主办了以“学习法理,弘扬法治”为主题的大赛,全校10000名学生都参加了此次大赛,赛后发现所有参赛学生的成绩均不低于50分且没有满分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩取整数,总分100分)进行分组,分别为组:;组:;组:;组:;组: , 并绘制了频数分布直方图. (1)、求出频数分布直方图中的值;(2)、判断这200名学生的成绩的中位数落在哪一组(直接写出结果);(3)、根据上述信息,估计全校10000名学生中成绩不低于70分的约有多少人.22. 已知二次函数的图象经过点 , 且对称轴为直线 .(1)、求的值;(2)、当时,求的最大值;(3)、平移抛物线 , 使其顶点始终在二次函数上,求平移后所得抛物线与轴交点纵坐标的最小值.23. 感知:数学课上,老师给出了一个模型:如图1,点在直线上,且 , 像这种一条直线上的三个顶点含有三个相等的角的模型我们把它称为“一线三等角”模型.
(1)、求出频数分布直方图中的值;(2)、判断这200名学生的成绩的中位数落在哪一组(直接写出结果);(3)、根据上述信息,估计全校10000名学生中成绩不低于70分的约有多少人.22. 已知二次函数的图象经过点 , 且对称轴为直线 .(1)、求的值;(2)、当时,求的最大值;(3)、平移抛物线 , 使其顶点始终在二次函数上,求平移后所得抛物线与轴交点纵坐标的最小值.23. 感知:数学课上,老师给出了一个模型:如图1,点在直线上,且 , 像这种一条直线上的三个顶点含有三个相等的角的模型我们把它称为“一线三等角”模型.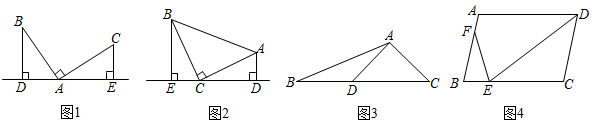 (1)、如图2,中, , , 直线经过点 , 过作于点 , 过作于点 . 求证:;(2)、如图3,在中,是上一点, , , , , 求点到边的距离;(3)、如图4,在中,为边上的一点,为边上的一点.若 , , , 求的值.
(1)、如图2,中, , , 直线经过点 , 过作于点 , 过作于点 . 求证:;(2)、如图3,在中,是上一点, , , , , 求点到边的距离;(3)、如图4,在中,为边上的一点,为边上的一点.若 , , , 求的值.