安徽省2022年名校联考三月份中考模拟数学试题

试卷更新日期：2022-04-18 类型：中考模拟

进入出卷网下载

一、单选题

1. 在﹣1、8、0、﹣2这四个数中，最小的数是（）

A、﹣1 B、8 C、0 D、﹣2

查看试题解析
2. 下列运算正确的是（）

A、 $x^{2} \cdot x^{3} = x^{6}$ B、 $2 a + 3 b = 5 a b$ C、 $(- 2 x)^{2} = - 4 x^{2}$ D、 $a^{8} \div a^{2} = a^{6}$

查看试题解析
3. 截至2018 年底，国家开发银行对“一带一路”沿线国家累积发放贷款超过1800 亿美元. 其中1800亿美元用科学记数法表示为（）

A、 $1.8 \times 1 0^{12}$ 美元 B、 $1.8 \times 1 0^{11}$ 美元 C、 $0.18 \times 1 0^{12}$ 美元 D、 $18 \times 1 0^{11}$ 美元

查看试题解析
4. 如图，将周长为 $12 c m$ 的 $△ A B C$ 沿边 $B C$ 向右平移 $3 c m$ 得到 $△ A^{'} B^{'} C^{'}$ ，则四边形 $A B C^{'} A^{'}$ 的周长为（）

A、 $17 c m$ B、 $18 c m$ C、 $19 c m$ D、 $20 c m$

查看试题解析
5. 如图，已知a//b，∠1＝73°，则∠2等于（）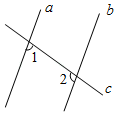

A、73° B、97° C、107° D、117°

查看试题解析
6. 把代数式 $a b^{2} - 6 a b + 9 a$ 分解因式，下列结果中正确的是（）

A、 $a (b + 3)^{2}$ B、 $a (b + 3) (b - 3)$ C、 $a (b - 4)^{2}$ D、 $a (b - 3)^{2}$

查看试题解析
7. 国家实行一系列“三农”优惠政策后，农民收入大幅度增加.某乡所辖村庄去年的月人均收入（单位：百元）情况如下表：

年人均收入

2

3

4

5

6

村庄个数

2

1

2

3

1

该乡去年各村庄年人均收入的中位数、平均数分别是（）

A、4、3 B、4、4 C、5、4 D、5、5

查看试题解析
8.
如图，边长为a，b的矩形的周长为14，面积为10，则a²b+ab²的值为（　　）

A、140 B、70 C、35 D、24

查看试题解析
9. 如图，菱形ABCD的边长为2cm，动点E，F同时从点A都以1cm/s的速度出发，点E沿A→B→C路线，点F沿A→D→C路线运动，连接EF．设运动时间为ts，△AEF的面积为Scm²，则下列图象中能大致表示S与t的函数关系的是（）

A、 B、 C、 D、

查看试题解析
10. 如图，正方形ABCD边长为2，BM、DN分别是正方形的两个外角的平分线，点P，Q分别是平分线BM、DN上的点，且满足∠PAQ＝45°，连接PQ、PC、CQ．则下列结论：①BP•DQ＝3.6；②∠QAD＝∠APB；③∠PCQ＝135°；④ $B P^{2} + D Q^{2} = P Q^{2}$ ．其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. -0.008的立方根是。

查看试题解析
12. 命题“如果ab=0，那么a=0”是命题；命题“如果a=0，那么ab=0”是命题．

查看试题解析
13. 如图，直线 $y = \frac{\sqrt{3}}{3} x + \sqrt{3}$ 与x轴、y轴分别相交于A，B两点，圆心P的坐标为（1，0），⊙P与y轴相切于点O．若将⊙P沿x轴向左移动，当⊙P与该直线相交时，横坐标为整数的点P坐标为．

查看试题解析
14. 关于x的一元二次方程x²+（m²+4m）x+m²﹣m﹣1=0的两根互为相反数，则m= ．

查看试题解析

三、解答题

15. 计算： $- (- 2) + | - 2 | + {(\sqrt{2020} - 2)}^{0}$ ．

查看试题解析
16. 如图，在平面直角坐标系中， $△ A B C$ 的三个顶点的坐标为 $A (1 ， - 4) ， B (3 ， - 3) ， C (1 ， - 1)$
⑴将△ABC沿y轴向上平移5个单位，画出后得到的△A₁B₁C₁；
⑵将△ABC绕点O顺时针旋转90°画出转到的△A₂B₂C₂ ，并直写出点A到点A₂所经过的路径长．

查看试题解析
17. 有A、B两家复印社，A4纸复印计费方式如表：

A4纸复印计费方式
A复印社
复印页数不超过20页时，每页0.12元；复印页数超过20页时，
超过部分每页收费0.09元
B复印社
不论复印多少页，每页收费0.1元

(1)、若要用A4纸复印x（x＞20）页，用含有x的式子表示两个复印社的收费？

(2)、用A4纸复印30页时，选哪家复印社划算？能便宜多少钱？

查看试题解析
18. 一天，数学课外活动小组的同学们，带着皮尺去测量某河道因挖沙形成的“圆锥形坑”的深度，来评估这些坑道对河道的影响，如图是同学们选择（确保测量过程中无安全隐患）的测量对象，测量方案如下：
①先测出沙坑坑沿的圆周长34.54米；
②甲同学直立于沙坑坑沿的圆周所在的平面上，经过适当调整自己所处的位置，当他位于B时恰好他的视线经过沙坑坑沿圆周上一点A看到坑底S（甲同学的视线起点C与点A，点S三点共线），经测量：AB=1.2米，BC=1.6米．
根据以上测量数据，求圆锥形坑的深度（圆锥的高）．（π取3.14，结果精确到0.1米）

查看试题解析
19. 如图，直线了l₁：y₁=kx+b与反比例函数y₂= $\frac{k}{x}$ 相交于A（-1，4）和B（-4，a），直线l₂：y₃=-x+c与反比例函数y₂= $\frac{k}{x}$ 相交于B、C两点，交y轴于点D，连接OB、OC、OA．

(1)、求反比例函数的解析式和c的值．

(2)、求△BOC的面积．

查看试题解析
20. 如图，AB是⊙O的直径，点C，D在⊙O上，且AD平分∠CAB，过点D作AC的垂线，与AC的延长线相交于E，与AB的延长线相交于点F，连接BD

(1)、求证：EF与⊙O相切；

(2)、若⊙O的半径为3，AD=4 $\sqrt{2}$ ，求△ABD的面积．

查看试题解析
21. 2015年12月14—16日，上合组织峰会在郑州CBD举行，为向市民宣传会议期间保持环境卫生，某报社举行了“维护‘郑州蓝’，我为郑州添光彩”的征文活动．现有甲、乙两校学生各上交30篇征文，现将两班的各30篇征文的成绩（单位：分）统计如下：
甲校
等级
成绩（S）
频数
A
$90 < S \leq 100$
x
B
$80 < S \leq 90$
15
C
$70 < S \leq 80$
10
D
$S \leq 70$
3
合计
30
根据上面提供的信息，解答下列问题：

(1)、表中x= ，甲校学生成绩的中位数落在等级中；

(2)、扇形统计图中等级D部分的扇形圆心角n= ．

(3)、现报社决定从两校所有A等级成绩的学生中随机抽取2名同学的征文刊登在报纸上．求抽取到两名学生恰好来自同一学校的概率（请列树状图或列表求解）．

查看试题解析
22. 某学校打算用篱笆围成矩形的生物园饲养小兔

(1)、若篱笆的长为16m，怎样围可使小兔的活动范围最大；

(2)、求证：当矩形的周长确定时，则一边长为周长的 $\frac{1}{4}$ 时，矩形的面积最大.

查看试题解析
23. 如图，在平面直角坐标系中，直线AB分别交x轴、y轴于点A(a，0)点，B(0，b)，且a、b满足a²﹣4a+4+|2a﹣b|＝0，点P在直线AB的左侧，且∠APB＝45°．

(1)、求a、b的值；

(2)、若点P在x轴上，求点P的坐标；

(3)、若 $△ A B P$ 为直角三角形，求点P的坐标．

查看试题解析

等级	成绩（S）	频数
A	$90 < S \leq 100$	x
B	$80 < S \leq 90$	15
C	$70 < S \leq 80$	10
D	$S \leq 70$	3
合计		30

年人均收入	2	3	4	5	6
村庄个数	2	1	2	3	1