安徽省合肥市2022年九年级下学期中考数学模拟试题

试卷更新日期：2022-04-18 类型：中考模拟

进入出卷网下载

一、单选题

1. 在数0，2，-3，-1中，最小的数是（　　）

A、0 B、2 C、-3 D、-1

查看试题解析
2. 计算 ${(- a)}^{2} \cdot {(- a)}^{3}$ 的结果正确的是（）

A、 $a^{5}$ B、 $a^{6}$ C、 $- a^{5}$ D、 $- a^{6}$

查看试题解析
3. 1月4日，2022年第一批全省重大项目集中开工动员会在合肥举行，此次集中开工重大项目共有731个，总投资约3761亿元．其中“3761亿”用科学记数法表示为（）

A、 $3.761 × 1 0^{10}$ B、 $3761 × 1 0^{8}$ C、 $3.761 × 1 0^{11}$ D、 $0.3761 × 1 0^{12}$

查看试题解析
4. 如图所示是一个放在水平面上的几何体，它的主视图是（）

A、 B、 C、 D、

查看试题解析
5. 如图，五边形ABCDE是正五边形， $A F ∥ D G$ ，若 $∠ 2 = 20 °$ ，则 $∠ 1 =$ （）

A、60° B、56° C、52° D、40°

查看试题解析
6. 李明明同学利用业余时间在小区摆地摊，他对某一周7天的收入数据进行分析，并列出方差公式： $s^{2} = \frac{1}{7} × [{(90 - \bar{x})}^{2} × 2 + {(100 - \bar{x})}^{2} × 3 + {(110 - \bar{x})}^{2} × 2]$ ，则该组数据的平均数与众数分别（）

A、100，100 B、100，90 C、110，110 D、110，100

查看试题解析
7. 如图， $△ A B C$ 中，AD平分 $∠ B A C$ ， E是BC中点， $A D ⊥ B D$ ， $A C = 7$ ， $A B = 4$ ，则DE的值为（）

A、1 B、2 C、 $\frac{1}{2}$ D、 $\frac{3}{2}$

查看试题解析
8. 若 $m > n > 0$ ，则下列代数式的值最大的是（）

A、4mn B、 $m^{2} + 4 n^{2}$ C、 $4 m^{2} + n^{2}$ D、 ${(m - n)}^{2}$

查看试题解析
9. 如图， $A D ∥ B C$ ， AC与BD交于点O，过点O作 $E F ∥ A D$ ，分别交AB，CD于点E，F，则下列结论不正确的是（）

A、 $\frac{A E}{B E} = \frac{D F}{C F}$ B、 $\frac{1}{A D} + \frac{1}{B C} = \frac{1}{O E}$ C、 $\frac{1}{A D} + \frac{1}{B C} = \frac{1}{O F}$ D、 $\frac{A D}{E F} = \frac{E F}{B C}$

查看试题解析
10. 如图， $△ A B C$ 和四边形DEFG分别是直角三角形和矩形， $∠ A = 90 °$ ， $A B = 4$ cm， $A C = 3$ cm， $F G ⊥ B C$ 于点B．若矩形DEFG从点B开始以每秒1cm的速度向右平移至点C，且矩形的边FG扫过 $△ A B C$ 的面积为S（ $c m^{2}$ ），平移的时间为t（秒），则S与t之间的函数图象可能是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 不等式 $4 x > 5 x - 2$ 的解集为．

查看试题解析
12. 因式分解： $a^{2} b - 6 a b + 9 b =$ ．

查看试题解析
13. 如图，一次函数 $y = k x$ 与反比例函数 $y = \frac{k}{x}$ 上的图象交于A，C两点， $A B ∥ y$ 轴， $B C ∥ x$ 轴，若 $△ A B C$ 的面积为4，则 $k =$ ．

查看试题解析

三、解答题

14. 如图，点E是菱形ABCD的边AD的中点，点F是AB上的一点，点G是BC上的一点，先以CE为对称轴将 $△ C D E$ 折叠，使点D落在CF上的点D'处，再以EF为对称轴折叠 $△ A E F$ ，使得点A的对应点 $A^{'}$ 与点 $D^{'}$ 重合，以FG为对称轴折叠 $△ B F G$ ，使得点B的对应点B'落在CF上．

(1)、写出图中一组相似三角形（除全等三角形）：

(2)、若 $∠ A = 60 °$ ，则 $\frac{F G}{C E}$ 的值为．

查看试题解析
15. 计算： $2 s i n 45 ° \cdot c o s 45 ° + {(\sqrt{2} - 1)}^{0} - \sqrt[3]{- 8}$ ．

查看试题解析
16. 如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点O，直线l和格点 $△ A B C$ （顶点是网格线的交点）．

(1)、以点O为旋转中心，将 $△ A B C$ 顺时针旋转90°得到 $△ A_{1} B_{1} C_{1}$ ，请画出 $△ A_{1} B_{1} C_{1}$ ；

(2)、画出 $△ A_{2} B_{2} C_{2}$ ，使得 $△ A B C$ 与 $△ A_{2} B_{2} C_{2}$ 关于直线l对称；

(3)、计算： $△ A_{2} B_{2} C_{2}$ 的面积= ．

查看试题解析
17. 已知甲市有1200名幼儿教师，乙市有800名幼儿教师，现新招聘590名新幼儿教师去这两市上岗若新招聘幼儿教师分配后，乙市的幼儿教师人数是甲市幼儿教师人数的 $\frac{3}{4}$ ，则分配甲、乙两市各多少名新招聘幼儿教师？

查看试题解析
18. 观察下列等式：
第1个等式： $\frac{1}{1 \times 2} + \frac{1 - 2}{1 + 1} + 1 = 1$ ；
第2个等式： $\frac{1}{2 \times 3} + \frac{4 - 2}{4 + 2} + \frac{1}{2} = 1$ ；
第3个等式： $\frac{1}{3 \times 4} + \frac{9 - 2}{9 + 3} + \frac{1}{3} = 1$ ；
第4个等式： $\frac{1}{4 \times 5} + \frac{16 - 2}{16 + 4} + \frac{1}{4} = 1$ ；
第5个等式： $\frac{1}{5 \times 6} + \frac{25 - 2}{25 + 5} + \frac{1}{5} = 1$ ；
……
按照以上规律，解决下列问题：

(1)、写出第6个等式：；

(2)、写出你猜想的第n个等式：（用含n的等式表示），并证明．

查看试题解析
19. 如图1是一辆消防车工作的瞬间，图2是其示意简图，AD是车身高度，且垂直地平面DE，从点A观察点B的仰角 $∠ 1 = 34 °$ ， CE垂直DE于点E．已知 $∠ A B C = 116 °$ ， $A D = 2$ 米， $A B = 6$ 米， $B C = 3$ 米，求DE和CE的长．（结果精确到0.1米，参考数据： $s i n 34 ° \approx 0.56$ ， $c o s 34 ° \approx 0.83$ ， $\sqrt{3} \approx 1.732$ ）

查看试题解析
20. 如图，点A，C是 $⊙ O$ 上的点，且 $∠ A O C = 90 °$ ，过点A作 $A B ⊥ O A$ ，连接BC交 $⊙ O$ 于点D，点D是BC的中点．

(1)、求 $∠ B$ 的度数；

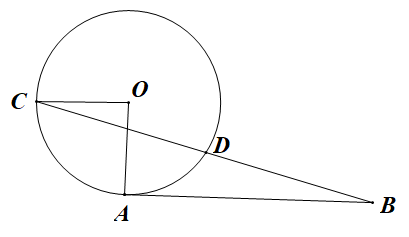(2)、求 $\frac{A B}{O C}$ 的值．

查看试题解析
21. 为了调查某地区九年级学生的身体素质情况，随机抽查了部分九年级学生进行体能测试，并依据其中仰卧起坐测试（次数/分钟）的结果绘制统计图表如下（不完整）：
组别
次数段
频数
频率
1
$0 \leq x < 15$
5
0.1
2
$15 \leq x < 30$
12
0.24
3
$30 \leq x < 45$
a
m
4
$45 \leq x < 60$
b
n
5
$60 \leq x < 75$
4
0.08

(1)、将统计表中的数据补充完整： $a =$ ， $b =$ ， $m =$ ， $n =$ ；

(2)、若该地区九年级有12000名学生，请估算该地区九年级每分钟仰卧起坐次数多于45次的学生数；

(3)、若测试结果大于60次（含60次）为优秀，需要抽取其中两名同学进行复核，已知优秀的学生中含有2个女生，求恰好抽到同性别学生的概率．

查看试题解析
22. 已知关于x的二次函数 $y = x^{2} - 2 a x + a^{2} + 2 a$ ．

(1)、当 $a = 1$ 时，求已知二次函数对应的抛物线的顶点和对称轴；

(2)、当 $a = 2$ 时，直线 $y = 2 x$ 与该抛物线相交，求抛物线在这条直线上所截线段的长度；

(3)、若抛物线 $y = x^{2} - 2 a x + a^{2} + 2 a$ 与直线 $x = 4$ 交于点A，求点A到x轴的最小值．

查看试题解析
23. 如图， $△ A B C$ 是等腰直角三角形，AD是其斜边BC上的高，点E是AD上的一点，以CE为边向上作等边 $△ C E F$ ，连接BF．

(1)、如图1，求 $∠ C B F$ 的度数；

(2)、连接AF，如图2，若 $E F ∥ A B$ ， BF与AC交于点G．
①证明：AF²=AG $\cdot$ AB；
②若BC=2，求FG的长．

查看试题解析

组别	次数段	频数	频率
1	$0 \leq x < 15$	5	0.1
2	$15 \leq x < 30$	12	0.24
3	$30 \leq x < 45$	a	m
4	$45 \leq x < 60$	b	n
5	$60 \leq x < 75$	4	0.08