安徽省亳州市2022年中考第一次模拟考试数学试题
试卷更新日期:2022-04-18 类型:中考模拟
一、单选题
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 计算的结果为( )A、 B、 C、 D、3. 如图所示的几何体是由5个大小相同的小立方块搭成的,该几何体的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 若 , 且 , 则的值等于( )A、 B、1 C、 D、-15. 不等式5x-3(2x-2)>5的解集在数轴上表示出来应为( )A、
4. 若 , 且 , 则的值等于( )A、 B、1 C、 D、-15. 不等式5x-3(2x-2)>5的解集在数轴上表示出来应为( )A、 B、
B、 C、
C、 D、
D、 6. 将一对直角三角板如图放置,点C在的延长线上,点B在上, , , , , 则( )
6. 将一对直角三角板如图放置,点C在的延长线上,点B在上, , , , , 则( ) A、 B、 C、 D、7. 为了解某校八年级400名学生的跳绳情况(60秒跳绳的次数),随机对该年级50名学生进行了调查,根据收集的数据绘制了如图所示的频数分布直方图(每组数据包括左端值不包括右端值,如最左边第一组的次数x为:),则以下说法正确的是( )
A、 B、 C、 D、7. 为了解某校八年级400名学生的跳绳情况(60秒跳绳的次数),随机对该年级50名学生进行了调查,根据收集的数据绘制了如图所示的频数分布直方图(每组数据包括左端值不包括右端值,如最左边第一组的次数x为:),则以下说法正确的是( )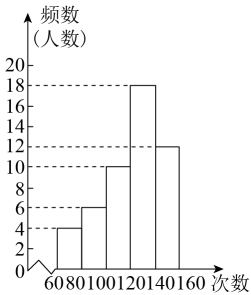 A、跳绳次数不少于100次的占80% B、大多数学生跳绳次数在140~160范围内 C、跳绳次数最多的是160次 D、由样本可以估计全年级400人中跳绳次数在60~80次的大约有48人8. 某企业因生产转型,二月份产值比一月份下降了20%,转型成功后产值呈现良好上升势头,四月份比一月份增长15.2%,若三、四、五月份的增长率相同,则五月份与一月份相比增长的百分数约为( )A、32% B、34% C、36% D、38%9. 已知反比例函数y=的图象如图所示,则一次函数y=cx+a和二次函数y=ax2﹣bx+c在同一直角坐标系中的图象可能是( )
A、跳绳次数不少于100次的占80% B、大多数学生跳绳次数在140~160范围内 C、跳绳次数最多的是160次 D、由样本可以估计全年级400人中跳绳次数在60~80次的大约有48人8. 某企业因生产转型,二月份产值比一月份下降了20%,转型成功后产值呈现良好上升势头,四月份比一月份增长15.2%,若三、四、五月份的增长率相同,则五月份与一月份相比增长的百分数约为( )A、32% B、34% C、36% D、38%9. 已知反比例函数y=的图象如图所示,则一次函数y=cx+a和二次函数y=ax2﹣bx+c在同一直角坐标系中的图象可能是( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 在四边形中, , , , , 点P在上运动,则取最小值时,边AP上的高是( )
10. 在四边形中, , , , , 点P在上运动,则取最小值时,边AP上的高是( )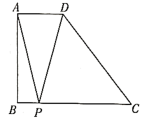 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 根据安徽省统计局数据,2021年安徽GDP约为43000亿元,同比增长8.3%,增速比全国(8.1%)快0.2个百分点,居全国第8位.将43000用科学记数法表示为 .12. 因式分解:2a2﹣4ab+2b2= .13. 如图,若的半径为 , , , , 则的长为 .
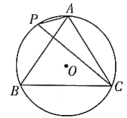
三、解答题
-
14. 如图,四边形为平行四边形,的平分线交于点F,交的延长线于点E,且 .
 (1)、若 , 则;(2)、若 , , 则 .15. 计算: .16. 《孙子算经》是我国古代经典数学名著.其中一个问题:今有三人共车,二车空;二人共车,九人步,问人与车各几何?这道题的意思是:有若干人乘车,每3人乘一车,最终剩余2辆车;若每2人乘一车,最终剩余9人无车可乘,问有多少人,多少辆车?17. 一棵大树AB(假定大树AB垂直于地面)被刮倾斜15°后折断在地上,树的顶部恰好接触到地面D处(如示意图所示),量得大树的倾斜角∠BAC=15°,大树被折断部分和地面所成的角∠ADC=60°,AD=4米,求大树AB原来的高度是多少米?(结果保留整数,参考数据:≈1.4,≈1.7,≈2.4)
(1)、若 , 则;(2)、若 , , 则 .15. 计算: .16. 《孙子算经》是我国古代经典数学名著.其中一个问题:今有三人共车,二车空;二人共车,九人步,问人与车各几何?这道题的意思是:有若干人乘车,每3人乘一车,最终剩余2辆车;若每2人乘一车,最终剩余9人无车可乘,问有多少人,多少辆车?17. 一棵大树AB(假定大树AB垂直于地面)被刮倾斜15°后折断在地上,树的顶部恰好接触到地面D处(如示意图所示),量得大树的倾斜角∠BAC=15°,大树被折断部分和地面所成的角∠ADC=60°,AD=4米,求大树AB原来的高度是多少米?(结果保留整数,参考数据:≈1.4,≈1.7,≈2.4) 18. 如图,给出了格点 , 线段在网格线的交点上,且点C在线段上.
18. 如图,给出了格点 , 线段在网格线的交点上,且点C在线段上.
⑴将向右平移7个单位长度,得到 , 请画出;
⑵请画出关于对称的;
⑶连接 , 求的长度.
19. 用同样大小的两种不同颜色的正方形纸片,按如图方式拼成长方形:第①个图形中有2张正方形纸片;
第②个图形中有张正方形纸片;
第③个图形中有张正方形纸片;
第④个图形中有张正方形纸片;

请你观察上述图形与算式,完成下列问题:
(1)、第⑤个图形中有张正方形纸片(直接写出结果);根据上面的发现我们可以猜想:(用含n的代数式表示);(2)、根据你的发现计算: .20. 如图,为⊙O的直径,过点的切线与弦的延长线交于点 , 为半径,于点 , 连接 . (1)、求证:;(2)、若 , 求的长.21. 某校为了解学生每周课外阅读的情况,在本校随机抽取80名学生进行问卷调查,现将调查结果绘制成不完整的统计图表,请根据图表中的信息解答下列问题:
(1)、求证:;(2)、若 , 求的长.21. 某校为了解学生每周课外阅读的情况,在本校随机抽取80名学生进行问卷调查,现将调查结果绘制成不完整的统计图表,请根据图表中的信息解答下列问题:
组别
阅读时间x/h
频数(人数)
A
8
B
24
C
32
D
n
E
4小时以上
4
(1)、表中的n= , 中位数落在组;(2)、请补全频数分布直方图;(3)、该校准备召开阅读经验分享会,计划在E组学生中随机选出两人作经验交流.已知E组的四名学生中,七八年级各有1人,九年级有2人,请用树状图法或列表法求抽取的两名学生都来自九年级的概率.
