安徽省蚌埠市2022年九年级下学期第一次模拟数学试题
试卷更新日期:2022-04-18 类型:中考模拟
一、单选题
-
1. 如图是由7个相同的小正方体搭成的几何体,则该几何体的主视图是( )
 A、
A、 B、
B、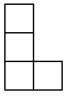 C、
C、 D、
D、 2. 某二次函数图象与二次函数的图象关于轴对称,该二次函数的解析式是( )A、 B、 C、 D、3. 如图,在菱形ABCD中,DE⊥AB,cosA= , AE=3,则tan∠DBE的值是( )
2. 某二次函数图象与二次函数的图象关于轴对称,该二次函数的解析式是( )A、 B、 C、 D、3. 如图,在菱形ABCD中,DE⊥AB,cosA= , AE=3,则tan∠DBE的值是( ) A、 B、2 C、 D、4. 如果两点和在反比例函数的图象上,那么与间的关系是( )A、 B、 C、 D、5. 已知圆锥的底面半径为4,母线长为6,则它的侧面展开图的面积是( )A、24 B、48 C、 D、6. 下列事件中,是确定事件的是( ) .A、打雷后会下雨 B、明天是睛天 C、1小时等于60分钟 D、下雨后有彩虹7. 如图,在平面直角坐标系中,以1.5为半径的圆的圆心P的坐标为 , 将沿y轴负方向平移1.5个单位长度,则x轴与的位置关系是( )
A、 B、2 C、 D、4. 如果两点和在反比例函数的图象上,那么与间的关系是( )A、 B、 C、 D、5. 已知圆锥的底面半径为4,母线长为6,则它的侧面展开图的面积是( )A、24 B、48 C、 D、6. 下列事件中,是确定事件的是( ) .A、打雷后会下雨 B、明天是睛天 C、1小时等于60分钟 D、下雨后有彩虹7. 如图,在平面直角坐标系中,以1.5为半径的圆的圆心P的坐标为 , 将沿y轴负方向平移1.5个单位长度,则x轴与的位置关系是( )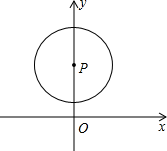 A、相交 B、相切 C、相离 D、无法确定8. 如图,中, , , , P是内部的一个动点,满足 , 则线段CP长的最小值为( )
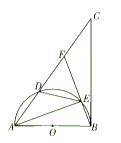
A、相交 B、相切 C、相离 D、无法确定8. 如图,中, , , , P是内部的一个动点,满足 , 则线段CP长的最小值为( ) A、 B、2 C、 D、9. 如图,已知⊙中, , , , 过点A作DF的垂线AE,垂足为点E,那么线段AE的长度为( )
A、 B、2 C、 D、9. 如图,已知⊙中, , , , 过点A作DF的垂线AE,垂足为点E,那么线段AE的长度为( ) A、 B、 C、 D、10. 如图,在矩形ABCD中,AB=5,BC=6,点E在BC边上,且BE=2,F为AB边上的一个动点,连接EF,以EF为边作等边△EFG,且点G在矩形ABCD内,连接CG,则CG的最小值为( )
A、 B、 C、 D、10. 如图,在矩形ABCD中,AB=5,BC=6,点E在BC边上,且BE=2,F为AB边上的一个动点,连接EF,以EF为边作等边△EFG,且点G在矩形ABCD内,连接CG,则CG的最小值为( )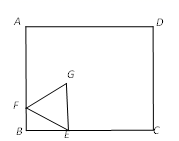 A、3 B、2.5 C、4 D、2
A、3 B、2.5 C、4 D、2二、填空题
-
11. 已知点P是线段AB的黄金分割点,AP>PB.若AB=10.则AP=(结果保留根号).12. ⊙O的直径AB=10cm,C为⊙O上不同于A,B一点,在△ABC中,∠B=30°,则AC长为cm.13. 如图,矩形 , 对角线与双曲线交于点D,若 , 则矩形的面积为 .
 14. 对于一个函数,自变量取时,函数值也等于 , 则称是这个函数的不动点.
14. 对于一个函数,自变量取时,函数值也等于 , 则称是这个函数的不动点.已知二次函数.
(1)、若3是此函数的不动点,则的值为.(2)、若此函数有两个相异的不动点 , , 且 , 则的取值范围为.三、解答题
-
15.
(1)、求x的值:5:(x+1)=3:x。(2)、已知线段a=2,b=8,求a,b的比例中项线段c。16. 一次数学活动课上,老师带领学生去测一条南北流向的河宽,如图所示,某学生在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西31°的方向上,沿河岸向北前行40米到达B处,测得C在B北偏西45°的方向上,请你根据以上数据,求这条河的宽度.(参考数值:tan31°≈ )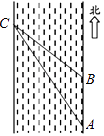 17. 如图,△ABC中,∠ABC=90°,以AB为直径的⊙O交AB于点D,点E为BC的中点,连接OD、DE.
17. 如图,△ABC中,∠ABC=90°,以AB为直径的⊙O交AB于点D,点E为BC的中点,连接OD、DE. (1)、求证:OD⊥DE.(2)、若∠BAC=30°,AB=8,求阴影部分的面积.18. 计算:19. 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)、求证:OD⊥DE.(2)、若∠BAC=30°,AB=8,求阴影部分的面积.18. 计算:19. 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).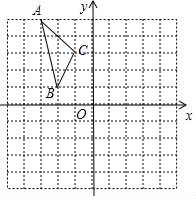
⑴画出△ABC和△A1B1C1关于原点O对称,画出△A1B1C1 , 并写出△A1B1C1的各顶点的坐标;
⑵将△ABC绕着点O按顺时针方向旋转90°得到的△A2B2C2 , 画出△A2B2C2 , 并写出△A2B2C2的各顶点的坐标.
20. 【问题】探究一次函数y=kx+k+1(k≠0)图象特点.
【探究】可做如下尝试:
y=kx+k+1=k(x+1)+1,当x=﹣1时,可以消去k,求出y=1.
【发现】结合一次函数图象,发现无论k取何值,一次函数y=kx+k+1的图象一定经过一个固定的点,该点的坐标是 ▲ ;
【应用】一次函数y=(k+2)x+k的图象经过定点P.
①点P的坐标是 ▲ ;
②已知一次函数y=(k+2)x+k的图象与y轴相交于点A,若△OAP的面积为3,求k的值.
21. 党的十八大以来,文山州牢固树立科学发展、绿色发展理念,把生态文明建设贯穿于经济、政治、文化和社会建设各个方面,深入实施“七彩云南文山保护行动”和“森林文山”建设.截止2017年底,全州共投入林业生态项目资金35亿元,完成了四项林业生态项目表示新一轮退耕还林,B表示石漠化治理,C表示天保工程森林管护,D表示天然商品林停伐的综合治理.并绘制出以下两幅不完整的统计图.请根据图中提供的信息,解答下列问题: (1)、此次林业生态项目共完成综合治理面积 ▲ 万亩.并将条形统计图补充完整;(2)、项目C占综合治理面积的百分比是多少?(3)、求扇形统计图中,项目D所对应的圆心角的度数.
(1)、此次林业生态项目共完成综合治理面积 ▲ 万亩.并将条形统计图补充完整;(2)、项目C占综合治理面积的百分比是多少?(3)、求扇形统计图中,项目D所对应的圆心角的度数.