安徽省安庆市2022年五校联考中考一模数学试题
试卷更新日期:2022-04-18 类型:中考模拟
一、单选题
-
1. 下列各数中,比-1小3的数字是( )A、-2 B、-4 C、0 D、22. 计算的结果是( )A、 B、 C、 D、3. 下面四个几何体中,左视图不是矩形的是( )A、
 B、
B、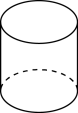 C、
C、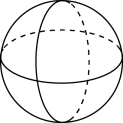 D、
D、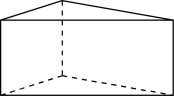 4. 安徽省2021年全省户籍人口7119.4万人,比上年增加36.5万人,其中7119.4万用科学记数法表示为( )A、 B、 C、 D、5. 下列一元二次方程中,没有实数根的是( )A、 B、 C、 D、6. 已知一次函数 , y随x的增大而增大,则k的值可以是( )A、-2 B、1 C、0 D、-37. 在某校九年级模拟考试中,1班的六名学生的数学成绩如下:104,116,110,118,116,90.下列关于这组数据的描述不正确的是( )A、众数是116 B、中位数是113 C、平均数是109 D、方差是868. 如图,在△ABC中,∠B=45°,AD⊥BC交BC于点D,若 , , 则BC=( )
4. 安徽省2021年全省户籍人口7119.4万人,比上年增加36.5万人,其中7119.4万用科学记数法表示为( )A、 B、 C、 D、5. 下列一元二次方程中,没有实数根的是( )A、 B、 C、 D、6. 已知一次函数 , y随x的增大而增大,则k的值可以是( )A、-2 B、1 C、0 D、-37. 在某校九年级模拟考试中,1班的六名学生的数学成绩如下:104,116,110,118,116,90.下列关于这组数据的描述不正确的是( )A、众数是116 B、中位数是113 C、平均数是109 D、方差是868. 如图,在△ABC中,∠B=45°,AD⊥BC交BC于点D,若 , , 则BC=( )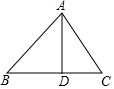 A、6 B、62 C、7 D、729. 如图,⊙O的内接四边形ABCD,AB是⊙O的直径,过点D的切线PD与AB的延长线交于点P,∠B=60°,则下列命题为假命题的是( )
A、6 B、62 C、7 D、729. 如图,⊙O的内接四边形ABCD,AB是⊙O的直径,过点D的切线PD与AB的延长线交于点P,∠B=60°,则下列命题为假命题的是( )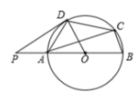 A、若 , 则PA=AD B、若∠BCD=120°,则△AOD是等边三角形 C、若 , 则四边形OBCD是菱形 D、若弦AC平分半径OD,则半径OD平分弦AC10. 如图,一个长方体铁块放置在圆柱形水槽容器内,向容器内按一定的速度均匀注水,60秒后将容器内注满.容器内水面的高度h(cm)与注水时间t(s)之间的函数关系图象大致是( )
A、若 , 则PA=AD B、若∠BCD=120°,则△AOD是等边三角形 C、若 , 则四边形OBCD是菱形 D、若弦AC平分半径OD,则半径OD平分弦AC10. 如图,一个长方体铁块放置在圆柱形水槽容器内,向容器内按一定的速度均匀注水,60秒后将容器内注满.容器内水面的高度h(cm)与注水时间t(s)之间的函数关系图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 计算:= .12. 分解因式的结果是 .13. 在同一个平面直角坐标系中,反比例函数与一次函数y=-x-1交于A、B两点,O为坐标原点,则△AOB的面积= .14. 将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展平纸片,如图(1);再次折叠该三角形纸片,使得点A与点D重合,折痕为EF,再次展平后连接DE、DF,如图2.解决下列问题:
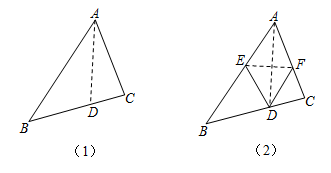 (1)、四边形AEDF的形状是;(2)、当∠BAC=60°时, .
(1)、四边形AEDF的形状是;(2)、当∠BAC=60°时, .三、解答题
-
15. 计算: .16. 如图,在由边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点分别是格点.

⑴将△ABC以点C为旋转中心旋转180°,画出旋转后对应的;
⑵将△ABC先左移2个单位,再下移4个单位,画出平移后的 .
17. 某工厂去年的总产值比总支出多90万元,今年比去年的总产值增加10%,总支出节约20%.如果今年的总产值比总支出多120万,那么去年的总产值和总支出分别是多少万元?18. 如图,东东和方方住在同一幢楼上,周末,他们在距离所住楼15米的点A处测得东东家(B点)的仰角为52°、方方家(C点)的仰角为35°.求东东家与方方垂直相隔多少米?(精确到0.1米).(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70;sin52°≈0.79,cos52°≈0.62,tan52°≈1.28)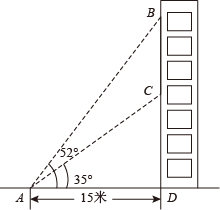 19. 观察以下等式:
19. 观察以下等式:第1个等式: , 第2个等式: , 第3个等式: ,
第4个等式: , ……,按照以上规律,解决下列问题:
(1)、写出第5个等式:;(2)、写出你猜想的第个等式: ▲ (用含n的等式表示,并证明).20. 如图,AB是⊙O的直径,AD是⊙O的切线,点C在⊙O上,OD∥BC交AC相交于点E.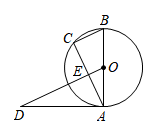 (1)、若AC=2CB,求证:△ABC≌△DAE;(2)、若AB=6,OD=8,求BC的长.21. 如图,在△ABC中,AB=AC,点D在BC上,DE∥AC,交AB于点E,点F在AC上,DC=DF,若BC=3,EB=4,CD=x,CF=y,求y与x的函数关系式,并写出自变量x的取值范围.
(1)、若AC=2CB,求证:△ABC≌△DAE;(2)、若AB=6,OD=8,求BC的长.21. 如图,在△ABC中,AB=AC,点D在BC上,DE∥AC,交AB于点E,点F在AC上,DC=DF,若BC=3,EB=4,CD=x,CF=y,求y与x的函数关系式,并写出自变量x的取值范围.

