辽宁省营口市2020-2021学年八年级下学期期末数学试题
试卷更新日期:2022-04-18 类型:期末考试
一、单选题
-
1. 下列各式是最简二次根式的是( )A、 B、 C、 D、2. 满足下列条件的三角形中,是直角三角形的是( )A、三个内角度数之比是3:4:5 B、三边长的平方比为5:12:13 C、三边长度是1: : D、三个内角度数比为2:3:43. 下列计算正确的是( )A、 B、=4 C、()2=6 D、=24. 2021年正值中国共产党建党100周年之际,某校开展“致敬建党百年,传承红色基因”党史知识竞赛活动.八年级甲、乙、丙、丁四个小组的同学分别参加了年级预赛,四个小组的平均分相同,若要从中选择出一个各成员实力更平均的小组代表年级参加学校决赛,那么应选( )
甲
乙
丙
丁
方差
3.6
3.2
4
4.3
A、甲组 B、乙组 C、丙组 D、丁组5. 如图,数轴上A点表示的数为-2,B点表示的数是1,过点B作 , 且 , 以点A为圆心,的长为半径作弧,弧与数轴的交点D表示的数为( ) A、 B、 C、 D、6. 一次函数y=kx+b(k≠0)与y=bx+k(b≠0)在同一直角坐标系内的图象大致是( )A、
A、 B、 C、 D、6. 一次函数y=kx+b(k≠0)与y=bx+k(b≠0)在同一直角坐标系内的图象大致是( )A、 B、
B、 C、
C、 D、
D、 7. 矩形ABCD与ECFG如图放置,点B , C , F共线,点C , E , D共线,连接AG , 取AG的中点H,连接EH . 若 , ,则 ( )
7. 矩形ABCD与ECFG如图放置,点B , C , F共线,点C , E , D共线,连接AG , 取AG的中点H,连接EH . 若 , ,则 ( )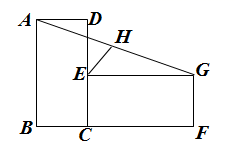 A、 B、2 C、 D、8. A、B两地相距 , 甲、乙两人沿同一条路从A地到B地. , 分别表示甲、乙两人离开A地的距离与时间之间的关系.对于以下说法正确的是( )
A、 B、2 C、 D、8. A、B两地相距 , 甲、乙两人沿同一条路从A地到B地. , 分别表示甲、乙两人离开A地的距离与时间之间的关系.对于以下说法正确的是( ) A、乙车出发1.5小时后甲才出发 B、两人相遇时,他们离开A地 C、甲的速度是 D、乙的速度是9. 如图,正方形的对角线相交于点 , 将正方形沿直线折叠,点C落在对角线上的E处,折痕与交于点G,则( )
A、乙车出发1.5小时后甲才出发 B、两人相遇时,他们离开A地 C、甲的速度是 D、乙的速度是9. 如图,正方形的对角线相交于点 , 将正方形沿直线折叠,点C落在对角线上的E处,折痕与交于点G,则( ) A、 B、 C、 D、10. 如图,等边的边长为 , 射线 , 点E从点A出发沿射线以的速度运动,点F从点B出发沿射线以的速度运动.设运动时间为 , 当t=( )s时,以A、C、E、F为顶点的四边形是平行四边形.
A、 B、 C、 D、10. 如图,等边的边长为 , 射线 , 点E从点A出发沿射线以的速度运动,点F从点B出发沿射线以的速度运动.设运动时间为 , 当t=( )s时,以A、C、E、F为顶点的四边形是平行四边形. A、1或2 B、2或3 C、2或4 D、2或6
A、1或2 B、2或3 C、2或4 D、2或6二、填空题
-
11. 函数y= 中自变量x的取值范围是 .12. 计算: .13. 北大附中实验学校科技节的作品得分包括三部分,专家评委给出的专业得分,宣传展示得分以及通过同学们投票得到的支持得分.已知某个作品各项得分如表所示(各项得分均按百分制计):按专业得分占50%、展示得分占40%、支持得分占10%,计算该作品的综合成绩(百分制),则该作品的最后得分是 .
项目
专业得分
展示得分
支持得分
成绩(分)
96
98
96
14. 如图,AB=BC,D在∠ABC外角平分线上,且CD⊥BC,△ABD的面积为12 cm2 , 则△BCD的面积为 cm2. 15. 如图,直线与相交于点P,则关于x的不等式的解集为 .
15. 如图,直线与相交于点P,则关于x的不等式的解集为 . 16. 如图,在平面直角坐标系中,菱形的顶点A在y轴正半轴上,顶点B,C在x轴上,且位于y轴两侧, , , 则对角线的长为 .
16. 如图,在平面直角坐标系中,菱形的顶点A在y轴正半轴上,顶点B,C在x轴上,且位于y轴两侧, , , 则对角线的长为 .
三、解答题
-
17. 计算题:(1)、+﹣+;(2)、(+)2×(5﹣2).18. 问题情境:“一粒米千滴汗,粒粒粮食汗珠换.”“为积极响应习近平总书记提出的坚决抵制餐饮浪费行为的重要指示,某送餐公司推出了“半份餐”服务,餐量是整份餐的一半,价格也是整份餐的一半,整份餐单价为16元,希望小学每天中午从该送餐公司订200份午餐,其中半份餐订 份( ),其余均为整份餐,该小学每天午餐订单总费用为 元.
 (1)、建立模型:求 与 之间的函数关系式;(2)、问题解决:若希望小学某天半份餐订了50份,求当天该小学午餐订单的总费用;(3)、已知某天希望小学午餐订单的总费用为2720元,当天订半份餐多少份?19. 一艘轮船从A港向南偏西48°方向航行到达B岛,再从B岛沿方向航行到达CA岛,A港到航线的最短距离是 .
(1)、建立模型:求 与 之间的函数关系式;(2)、问题解决:若希望小学某天半份餐订了50份,求当天该小学午餐订单的总费用;(3)、已知某天希望小学午餐订单的总费用为2720元,当天订半份餐多少份?19. 一艘轮船从A港向南偏西48°方向航行到达B岛,再从B岛沿方向航行到达CA岛,A港到航线的最短距离是 . (1)、若轮船速度为小时,求轮船从C岛沿返回A港所需的时间.(2)、C岛在A港的什么方向?20. “疫情远未结束,防疫绝不放松”.为了了解同学们掌握防疫知识的情况,增强防疫意识,某校举行了疫情防护知识测试活动,现从该校七、八年级各随机抽取20名学生的测试成绩(90分及以上为优秀)进行整理、描述和分析,以下是部分信息.
(1)、若轮船速度为小时,求轮船从C岛沿返回A港所需的时间.(2)、C岛在A港的什么方向?20. “疫情远未结束,防疫绝不放松”.为了了解同学们掌握防疫知识的情况,增强防疫意识,某校举行了疫情防护知识测试活动,现从该校七、八年级各随机抽取20名学生的测试成绩(90分及以上为优秀)进行整理、描述和分析,以下是部分信息.七年级20名学生的测试成绩:72,80,85,90,78,82,80,90,92,90,100,90,83,88,97,98,99,80,81,85.
八年级20名学生的测试成绩条形统计图如图:

【七、八年级抽取的学生的测试成绩的平均数、众数、中位数、90分及以上人数所占百分比如下表所示】:
年级
平均数
众数
中位数
90分及以上人数所占百分比
七年级
87
a
86.5
45%
八年级
87
94
b
c
根据以上信息,解答下列问题:
(1)、a=、b=、c=;(2)、根据上述数据,你认为该校七、八年级中,哪个年级掌握防疫知识更好?请说明理由;(3)、该校七、八年级共有3000名学生参加了此次测试活动,估计参加此次测试活动成绩优秀的学生有多少人?21. 如图,在四边形 中, ,对角线 、 交于点 ,且 ,过点 作 ,交 于点 ,交 于点 ,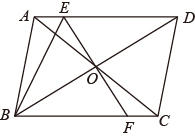 (1)、求证:四边形 为平行四边形;(2)、连接 ,若 , ,求 的度数.22. 如图,直线分别与x轴,y轴交于A、B两点,A、B的坐标分别为、 , 过点B的直线交x轴于点C,点是直线l上的一点,连接 .
(1)、求证:四边形 为平行四边形;(2)、连接 ,若 , ,求 的度数.22. 如图,直线分别与x轴,y轴交于A、B两点,A、B的坐标分别为、 , 过点B的直线交x轴于点C,点是直线l上的一点,连接 .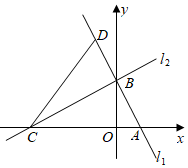 (1)、求的解析式;(2)、求C、D的坐标;(3)、求的面积.23. 正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.
(1)、求的解析式;(2)、求C、D的坐标;(3)、求的面积.23. 正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°. (1)、求证:EF=AE+CF(2)、当AE=1时,求EF的长.24. 某商场欲购进果汁饮料和碳酸饮料共50箱,两种饮料每箱的进价和售价如下表所示.设购进果汁饮料x箱(x为正整数),且所购进的两种饮料能全部卖出,获得的总利润为W元(注:总利润=总售价﹣总进价).
(1)、求证:EF=AE+CF(2)、当AE=1时,求EF的长.24. 某商场欲购进果汁饮料和碳酸饮料共50箱,两种饮料每箱的进价和售价如下表所示.设购进果汁饮料x箱(x为正整数),且所购进的两种饮料能全部卖出,获得的总利润为W元(注:总利润=总售价﹣总进价).饮料
果汁饮料
碳酸饮料
进价(元/箱)
51
36
售价(元/箱)
61
43
(1)、设商场购进碳酸饮料y箱,直接写出y与x的函数关系式;(2)、求总利润w关于x的函数关系式;(3)、如果购进两种饮料的总费用不超过2100元,那么该商场如何进货才能获利最多?并求出最大利润.25. 如图,四边形ABCD、BEFG均为正方形, (1)、(1)如图1,连接AG、CE,试判断AG和CE的数量和位置关系并证明.(2)、将正方形BEFG绕点B顺时针旋转β角(0°<β<180°),如图2,连接AG、CE相交于点M,连接MB,当角β发生变化时,∠EMB的度数是否发生变化?若不变化,求出∠EMB的度数;若发生变化,请说明理由.(3)、在(2)的条件下,过点A作AN⊥MB交MB的延长线于点N,请直接写出线段CM与BN的数量关系.
(1)、(1)如图1,连接AG、CE,试判断AG和CE的数量和位置关系并证明.(2)、将正方形BEFG绕点B顺时针旋转β角(0°<β<180°),如图2,连接AG、CE相交于点M,连接MB,当角β发生变化时,∠EMB的度数是否发生变化?若不变化,求出∠EMB的度数;若发生变化,请说明理由.(3)、在(2)的条件下,过点A作AN⊥MB交MB的延长线于点N,请直接写出线段CM与BN的数量关系.