内蒙古自治区乌海市2020-2021学年八年级下学期期末数学试题
试卷更新日期:2022-04-18 类型:期末考试
一、单选题
-
1. 化简 的结果是( )A、 B、 C、 D、2. 若代数式有意义,则x的取值范围是( )A、 B、 C、且 D、且3. 以下各组数为三角形的三边长,其中能够构成直角三角形的是( )A、 , , B、7,24,25 C、8,13,17 D、10,15,204. 如图,在平面直角坐标系中,点P坐标为(-2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
 A、-4和-3之间 B、3和4之间 C、-5和-4之间 D、4和5之间5. 平行四边形的两条对角线长分别为6和10,则平行四边形的一条边的长x的取值范围为( )A、4<x<6 B、2<x<8 C、0<x<10 D、0<x<66. 快递公司快递员小张一周内投递快递物品件数情况为:有4天是每天投递65件,有2天是每天投递70件,有1天是90件,这一周小张平均每天投递物品的件数为( )A、80件 B、75件 C、70件 D、65件7. 下列命题:①若 , 则 ②的算术平方根是2 ③对角线相等的四边形是矩形 ④一组数据5,6,7,8,9的中位数和众数都是7,其中真命题的个数是( )A、0 B、1 C、2 D、38. 如图,四边形是菱形,对角线 , 相交于点O,于点H,连接 , , 则的度数是( )
A、-4和-3之间 B、3和4之间 C、-5和-4之间 D、4和5之间5. 平行四边形的两条对角线长分别为6和10,则平行四边形的一条边的长x的取值范围为( )A、4<x<6 B、2<x<8 C、0<x<10 D、0<x<66. 快递公司快递员小张一周内投递快递物品件数情况为:有4天是每天投递65件,有2天是每天投递70件,有1天是90件,这一周小张平均每天投递物品的件数为( )A、80件 B、75件 C、70件 D、65件7. 下列命题:①若 , 则 ②的算术平方根是2 ③对角线相等的四边形是矩形 ④一组数据5,6,7,8,9的中位数和众数都是7,其中真命题的个数是( )A、0 B、1 C、2 D、38. 如图,四边形是菱形,对角线 , 相交于点O,于点H,连接 , , 则的度数是( ) A、 B、 C、 D、9. 四个点A,B,C,D在同一平面内,从①;②;③;④;⑤ , 这五个条件中任选三个,能使四边形是菱形的选法有( )A、1种 B、2种 C、3种 D、4种10. 若关于x的函数 是一次函数,则m的值为( )A、 B、 C、1 D、211. 已知点 、点 在一次函数 的图像上,且 ,则m的取值范围是( )A、 B、 C、 D、12. 如图,正方形ABCD的边长为4,点E在边AB上,AE=1,若点P为对角线BD上的一个动点,则△PAE周长的最小值是( )
A、 B、 C、 D、9. 四个点A,B,C,D在同一平面内,从①;②;③;④;⑤ , 这五个条件中任选三个,能使四边形是菱形的选法有( )A、1种 B、2种 C、3种 D、4种10. 若关于x的函数 是一次函数,则m的值为( )A、 B、 C、1 D、211. 已知点 、点 在一次函数 的图像上,且 ,则m的取值范围是( )A、 B、 C、 D、12. 如图,正方形ABCD的边长为4,点E在边AB上,AE=1,若点P为对角线BD上的一个动点,则△PAE周长的最小值是( ) A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题
-
13. 一组数据3,4,3,a,8的平均数为5,则这组数据的方差是 .14. 已知x,y为实数,且 , 则的值是 .15. 已知是直线上的点,则的值是 .16. 如图,在中, . 以点B为圆心,以小于长为半径作弧,分别交、于点P、Q,再分别以P、Q为圆心,以大于的长为半径作弧,两弧在内交于点M,连接并延长交于点E,则 .
 17. 如图所示,为的中位线,点F在上,且 , 若 , , 则的长为 .
17. 如图所示,为的中位线,点F在上,且 , 若 , , 则的长为 .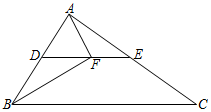 18. 如图,将矩形纸片ABCD沿MN折叠,使点B与点D重合,再将△CDN沿DN折叠.使点C恰好落在MN上的点F处.若MN=5,则AD的长为 .
18. 如图,将矩形纸片ABCD沿MN折叠,使点B与点D重合,再将△CDN沿DN折叠.使点C恰好落在MN上的点F处.若MN=5,则AD的长为 .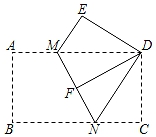 19. 如图,一次函数与一次函数的图像相交于点P,则关于x的不等式的解集为 .
19. 如图,一次函数与一次函数的图像相交于点P,则关于x的不等式的解集为 .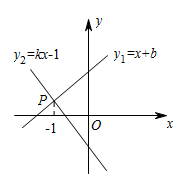 20. 如图,中, , 于点E,于点F, , 相交于点H,与的延长线相交于点G.下面给出四个结论:①;②;③;④ , 其中正确的结论是 .
20. 如图,中, , 于点E,于点F, , 相交于点H,与的延长线相交于点G.下面给出四个结论:①;②;③;④ , 其中正确的结论是 .
三、解答题
-
21. 计算:(1)、;(2)、 .22. 4月23日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”某校响应号召,鼓励师生利用课余时间广泛阅读,该校文学社为了解学生课外阅读的情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:
收集数据 从学校随机抽取20名学生,进行了每周用于课外阅读时间的调查,数据如下(单位:min):
30 60 81 50 40 110 130 146 90 100
60 81 120 140 70 81 10 20 100 81
(1)、整理数据 按如下分段整理样本数据并补全表格:课外阅读时间x(min)
等级
D
C
B
A
人数
3
8
(2)、分析数据 补全下列表格中的统计量:平均数
中位数
众数
80
(3)、得出结论用样本中的统计量估计该校学生每周用于课外阅读时间的情况等级为 ;
(4)、如果该校现有学生400人,估计等级为“B”的学生有多少名?(5)、假设平均阅读一本课外书的时间为160分钟,请你选择一种统计量估计该校学生每人一年 (按52周计算)平均阅读多少本课外书?23. 学校要在教学楼侧面悬挂中考励志的标语牌,如图所示,为了使标语牌醒目,计划设计标语牌的宽度为BC,为了测量BC,在距教学楼20米的升旗台P处利用测角仪测得教学楼AB的顶端点B的仰角为 ,点C的仰角为 ,求标语牌BC的宽度(结果保留根号) 24. 如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF,连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC
24. 如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF,连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC (1)、请判断:FG与CE的数量关系是 , 位置关系是;(2)、如图2,若点E、F分别是CB、BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请出判断判断并给予证明.25. 2021年3月20日,三星堆遗址考古新发现揭晓,出土文物500余件,三星堆考古发掘成果再次成为炙手可热的话题.某商家看准商机后,计划购进一批“考古盲盒”(三星堆文物模型盲盒)进行销售.已知该商家用1570元购进了10个甲种盲盒和15个乙种盲盒,甲种盲盒的进货单价比乙种盲盒的进货单价多2元.(1)、甲种盲盒和乙种盲盒的进货单价分别是多少元;(2)、由于“考古盲盒”畅销,商家决定再购进这两种盲盒共50个,其中甲种盲盒数量不多于乙种盲盒数量的2倍,且每种盲盒的进货单价保持不变.若甲种盲盒的销售单价为83元,乙种盲盒的销售单价为78元.
(1)、请判断:FG与CE的数量关系是 , 位置关系是;(2)、如图2,若点E、F分别是CB、BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请出判断判断并给予证明.25. 2021年3月20日,三星堆遗址考古新发现揭晓,出土文物500余件,三星堆考古发掘成果再次成为炙手可热的话题.某商家看准商机后,计划购进一批“考古盲盒”(三星堆文物模型盲盒)进行销售.已知该商家用1570元购进了10个甲种盲盒和15个乙种盲盒,甲种盲盒的进货单价比乙种盲盒的进货单价多2元.(1)、甲种盲盒和乙种盲盒的进货单价分别是多少元;(2)、由于“考古盲盒”畅销,商家决定再购进这两种盲盒共50个,其中甲种盲盒数量不多于乙种盲盒数量的2倍,且每种盲盒的进货单价保持不变.若甲种盲盒的销售单价为83元,乙种盲盒的销售单价为78元.①假设此次购进甲种盲盒的个数为a(个),售完这两批盲盒所获总利润为w(元),请写出w与a之间的函数关系式;
②商家如何安排第二批进货方案,才能使售完这两批盲盒获得总利润最大?最大利润是多少元?
26. 如图,在平面直角坐标系中,直线l1: 分别与x轴、y轴交于点B、C,且与直线l2: 交于点A.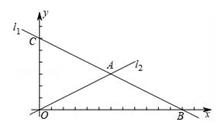 (1)、求出点A的坐标(2)、若D是线段OA上的点,且△COD的面积为12,求直线CD的解析式(3)、在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点P的坐标;若不存在,请说明理由.
(1)、求出点A的坐标(2)、若D是线段OA上的点,且△COD的面积为12,求直线CD的解析式(3)、在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点P的坐标;若不存在,请说明理由.