内蒙古自治区呼伦贝尔市扎兰屯市2020-2021学年八年级下学期期末数学试题

试卷更新日期：2022-04-18 类型：期末考试

进入出卷网下载

一、单选题

1. 下列式子中，一定属于二次根式的是（）

A、 $\sqrt{- 6}$ B、 $\sqrt{x - 2}$ C、 $\sqrt[3]{9}$ D、 $\sqrt{3}$

查看试题解析
2. 化简二次根式 $\sqrt{- a^{3}}$ 的正确结果是（）

A、 $a \sqrt{- a}$ B、 $a \sqrt{a}$ C、 $- a \sqrt{- a}$ D、 $- a \sqrt{a}$

查看试题解析
3. 在下列式子中，表示y是x的正比例函数的是（）．

A、 $y = \sqrt{x}$ B、 $y = x^{2}$ C、 $y = \frac{x}{2}$ D、 $y = \frac{2}{x}$

查看试题解析
4. 下列说法正确的是（　　）

A、对角线互相垂直的四边形是菱形 B、矩形的对角线互相垂直 C、一组对边平行的四边形是平行四边形 D、对角线相等的平行四边形是矩形

查看试题解析
5. 如图，在Rt△ABC中，∠ACB=90°，CM是斜边AB上的中线，E、F分别为MB、BC的中点，若EF=1，则AB等于（　）

A、3 B、 $\frac{7}{2}$ C、4 D、 $\frac{9}{2}$

查看试题解析
6. 如图，直线 $y = k x + b$ 与坐标轴的两交点分别为 $A (2 ， 0)$ 和 $B (0 ， - 3)$ ，则不等式 $k x + b + 3$ > $0$ 的解集为（）

A、x>0 B、x<0 C、x>2 D、x<2

查看试题解析
7. 一次函数y＝kx﹣2（k≠0）的函数值y随x增大而减小，那么该函数的图象不经过（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
8. 将直线 $y = - 2 x - 2$ 向右平移1个单位长度，可得直线的表达式为（）

A、 $y = 2 x$ B、 $y = - 2 x - 4$ C、 $y = - 2 x$ D、 $y = - 2 x + 4$

查看试题解析
9. 如下图，在 $R t △ A B C$ 中， $∠ B A C = 90 °$ ， D、E分别是 $A B$ 、 $B C$ 的中点，F在 $C A$ 延长线上， ∠FDA=∠B，AC=6，AB=8，则四边形 $A E D F$ 的周长为（）

A、 $14$ B、 $15$ C、 $16$ D、 $18$

查看试题解析
10. 如图，在矩形ABCD中，AD=m，E是AD边上的一个动点，点F，G，H分别是BC，BE，CE的中点．当四边形EGFH为正方形时， $S_{矩形 A B C D} ： S_{正方形 E G F H} =$ （）

A、4：1 B、1：4 C、5：2 D、2：1

查看试题解析
11. “清明节”期间，小海自驾去某地祭祖，如图是他们汽车行驶的路程y（千米）与汽车行驶时间x（小时）之间的函数图象．汽车行驶2小时到达目的地，这时汽车行驶了（）千米．

A、120 B、130 C、140 D、150

查看试题解析
12. 如图，已知直线 $l_{1} ：$ $y$ ＝ $3 x + 1$ 和直线 $l_{2} ：$ $y$ ＝ $m x + n$ 交于点 $P (a ， - 8)$ ，则关于x的不等式 $3 x + 1$ < $m x + n$ 的解集为（　　）

A、 $x$ > $3$ B、 $x$ < $- 3$ C、 $x$ < $- 8$ D、 $x$ > $- 8$

查看试题解析

二、填空题

13. 使式子 $\frac{\sqrt{3 - 5 x}}{x + 1}$ 有意义的x的取值范围是．

查看试题解析
14. 甲、乙两名同学参加古诗词大赛，五次比赛成绩的平均分都是90分，如果方差分别为 $S_{甲} {^{2}}_{}$ =20， $S_{乙}^{2}$ =16，则比赛成绩比较稳定的是．（填“甲”或“乙”）

查看试题解析
15. 直角三角形两条直角边长分别为2和4，则斜边上的中线长为．

查看试题解析
16. 如图， $A C$ 是边长为2的正方形 $A B C D$ 的对角线， $P$ 为 $B C$ 边上一动点， $E$ ， $F$ 为 $A B$ ， $A C$ 的中点.当 $P E + P F$ 的值最小时， $C P$ 的值为.

查看试题解析

三、解答题

17. 计算： $(4 \sqrt{2} - 3 \sqrt{6}) \div 2 \sqrt{2}$ ．

查看试题解析
18. 如图所示，四边形ABCD是平行四边形，E，F分别是对角线AC上的两点， ∠1=∠2．求证：四边形BEDF为平行四边形．

查看试题解析
19. 如图，小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙脚的距离为0.7米，顶端距离地面2.4米．如果保持梯子底端位置不动，将梯子斜靠在右墙时，顶端距离地面2米，求小巷的宽度．

查看试题解析
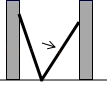20. 甲、乙两车从A地出发前往B地．两车离开A地的距离 $y (k m)$ 与时间 $x (h)$ 的关系如图所示．

(1)、A、B两地之间的距离为km，乙车的平均速度是km/h；

(2)、求图中a的值；

(3)、求甲车出发多长时间，两车相距20km．

查看试题解析
21. 为传承中华文化，激发学生爱国情怀，提高学生对中华民族的文化自信，某学校组织了一次“传统文化知识”竞赛，每班各选40名同学参加比赛，成绩分别为A，B，C，D四个等级，其中相应等级的得分依次记为100分、90分、80分、70分，学校将九年级一班和二班的成绩整理并绘制成如下两幅统计图．

(1)、请将一班竞赛成绩统计图补充完整．

(2)、求出下表中a，b，c的值．

平均数
中位数
众数
一班
a
90
c
二班
88
b
90

(3)、根据（2）中的数据，请你对这次竞赛成绩的结果进行分析．

查看试题解析
22. 如图，在平面直角坐标系中，直线l₁：y＝k₁x＋b（k₁≠0）经过点A（4，0），B（0，2），与直线l2：y＝k₂x（k₂≠0）交于点P（a，1）．

(1)、求直线l₁、l₂的表达式；

(2)、C为直线 $l_{1}$ 上一点，过点C作直线m⊥x轴于E，直线m交l2于点D．当CD＝3ED时，求C点的坐标．

查看试题解析
23. 如图，在△ABC中， BC=a，AC=b，AB=c，若∠C为直角，如图1，则有结论： $a^{2} + b^{2} = c^{2}$ ；当∠C为锐角（如图2）或钝角（如图3）时，请你完成下列探究：

(1)、分别猜想∠C为锐角或钝角这两种情况下 $a^{2} + b^{2}$ 与 $c^{2}$ 的大小关系；

(2)、任选（1）中的一个猜想进行证明．

查看试题解析

	平均数	中位数	众数
一班	a	90	c
二班	88	b	90