内蒙古自治区呼伦贝尔市满洲里市2020-2021学年八年级下学期期末数学试题
试卷更新日期:2022-04-18 类型:期末考试
一、单选题
-
1. 下列各式一定是二次根式的是( )A、 B、 C、 D、2. 四边形中, . 要判别四边形是平行四边形,还需满足条件( )
 A、 B、 C、 D、3. 以下列长度的线段为边 ,不能组成直角三角形的是 ( ).A、1,1, B、 , , C、2,3,4 D、8,15,174. 若 ,则 的值为( )A、2 B、 C、 D、5. 下列各曲线中不能表示y是x的函数的是( )A、
A、 B、 C、 D、3. 以下列长度的线段为边 ,不能组成直角三角形的是 ( ).A、1,1, B、 , , C、2,3,4 D、8,15,174. 若 ,则 的值为( )A、2 B、 C、 D、5. 下列各曲线中不能表示y是x的函数的是( )A、 B、
B、 C、
C、 D、
D、 6. 如图,在 中, , , ,点D,E,F分别是AB,BC,CA的中点,连结DE,EF,则四边形ADEF的周长为( )
6. 如图,在 中, , , ,点D,E,F分别是AB,BC,CA的中点,连结DE,EF,则四边形ADEF的周长为( ) A、6 B、9 C、12 D、157. 15名学生演讲赛的成绩各不相同,若某选手想知道自己能否进入前8名,则他不仅要知道自己的成绩,还应知道这15名学生成绩的( )A、平均数 B、众数 C、方差 D、中位数8. 如图,分别以直角 三边为边向外作三个正方形,其面积分别用 表示,若 , ,那么 ( )
A、6 B、9 C、12 D、157. 15名学生演讲赛的成绩各不相同,若某选手想知道自己能否进入前8名,则他不仅要知道自己的成绩,还应知道这15名学生成绩的( )A、平均数 B、众数 C、方差 D、中位数8. 如图,分别以直角 三边为边向外作三个正方形,其面积分别用 表示,若 , ,那么 ( ) A、9 B、5 C、53 D、459. 已知一次函数 的函数值 随 的增大而增大,则该函数的图象大致是( )A、
A、9 B、5 C、53 D、459. 已知一次函数 的函数值 随 的增大而增大,则该函数的图象大致是( )A、 B、
B、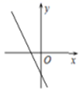 C、
C、 D、
D、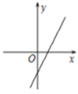 10. 一个直角三角形两条直角边的长分别为6,8,则其斜边上的高为( )A、 B、13 C、 D、2511. 对于函数y=- x+1,下列结论正确的是( )A、它的图象不经过第四象限 B、y的值随x的增大而增大 C、它的图象必经过点(0,1) D、当x>2时,y>012. 某单位招聘一名员工,从专业知识、工作业绩、面试成绩三个方面进行考核(考核的满分均为100分)方面的权重比依次为2∶4∶4.小明经过考核后所得的分数依次为90,85,80分,那么小明考核的最后得分是( )A、80 B、84 C、87 D、90
10. 一个直角三角形两条直角边的长分别为6,8,则其斜边上的高为( )A、 B、13 C、 D、2511. 对于函数y=- x+1,下列结论正确的是( )A、它的图象不经过第四象限 B、y的值随x的增大而增大 C、它的图象必经过点(0,1) D、当x>2时,y>012. 某单位招聘一名员工,从专业知识、工作业绩、面试成绩三个方面进行考核(考核的满分均为100分)方面的权重比依次为2∶4∶4.小明经过考核后所得的分数依次为90,85,80分,那么小明考核的最后得分是( )A、80 B、84 C、87 D、90二、填空题
-
13. 若 , 则 .14. 已知,正比例函数y=kx的图象经过点(a,b),且=2,则k的值等于 .15. 已知x1 , x2 , …,xn的方差为2,则2x1 , 2x2 , …,2xn的方差为 .16. 如图,△ABC中,∠C=90°,AD平分∠BAC,AB=5,AC=3,则BD的长是 .
 17. 如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于点E,F,连接PB,PD.若AE=2,PF=8.则图中阴影部分的面积为.
17. 如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于点E,F,连接PB,PD.若AE=2,PF=8.则图中阴影部分的面积为.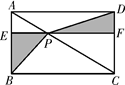
三、解答题
-
18. 计算: .19.20. 如图,在四边形 中,点 是对角线 的中点, , , , . 是直角三角形吗?若是请说明理由.
 21. 已知:y与x+2成正比例,且x=﹣4时,y=﹣2;(1)、求y与x之间的函数表达式;(2)、点P1(m,y1),P2(m﹣2,y2)在(1)中所得函数图象上,比较y1与y2的大小.22. 如图,在等腰三角形ABC中,于点H,点E是AH上一点,延长AH至点F,使.求证:四边形EBFC是菱形.
21. 已知:y与x+2成正比例,且x=﹣4时,y=﹣2;(1)、求y与x之间的函数表达式;(2)、点P1(m,y1),P2(m﹣2,y2)在(1)中所得函数图象上,比较y1与y2的大小.22. 如图,在等腰三角形ABC中,于点H,点E是AH上一点,延长AH至点F,使.求证:四边形EBFC是菱形. 23. 我市某中学举行“校园好声音”歌手大赛,甲、乙两班根据本班初赛成绩各选出5名选手组成甲班代表队和乙班代表队参加学校预赛,两个队各选出的5名选手的预赛成绩(满分100)如图所示:
23. 我市某中学举行“校园好声音”歌手大赛,甲、乙两班根据本班初赛成绩各选出5名选手组成甲班代表队和乙班代表队参加学校预赛,两个队各选出的5名选手的预赛成绩(满分100)如图所示:根据图示信息,整理分析数据如表:
平均数(分)
中位数(分)
众数(分)
方差
甲班
a
85
c
70
乙班
85
b
100
160
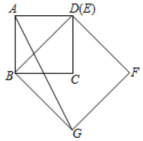
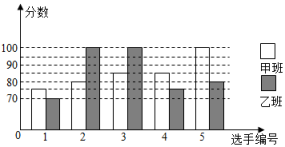 (1)、填空:甲班2号选手的预赛成绩是分,乙班3号选手的预赛成绩是分,班的预赛成绩更平衡,更稳定;(2)、求出表格中a= , b= , c=;(3)、学校决定在甲、乙两班中选取预赛成绩较好的5人参加该活动的区级比赛,求这5人预赛成绩的平均分数.24. 在边长为5的正方形ABCD中,点E在边CD所在直线上,连接BE,以BE为边,在BE的下方作正方形BEFG,并连接AG.如图,当点E与点D重合时,求AG的长.
(1)、填空:甲班2号选手的预赛成绩是分,乙班3号选手的预赛成绩是分,班的预赛成绩更平衡,更稳定;(2)、求出表格中a= , b= , c=;(3)、学校决定在甲、乙两班中选取预赛成绩较好的5人参加该活动的区级比赛,求这5人预赛成绩的平均分数.24. 在边长为5的正方形ABCD中,点E在边CD所在直线上,连接BE,以BE为边,在BE的下方作正方形BEFG,并连接AG.如图,当点E与点D重合时,求AG的长.