内蒙古自治区呼伦贝尔市阿荣旗2020-2021学年八年级下学期期末数学试题
试卷更新日期:2022-04-18 类型:期末考试
一、单选题
-
1. 函数y= 中,自变量x的取值范围是( )A、x≥1 B、x>1 C、x≥1且x≠2 D、x≠22. 下列图象中,表示y不是x的函数的是( )A、
 B、
B、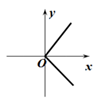 C、
C、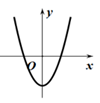 D、
D、 3. 由下列条件不能判定 为直角三角形的是( )A、 B、 C、 D、 , ,4. 根式中,最简二次根式有( )A、1个 B、2个 C、3个 D、4个5. 若关于x的函数 是一次函数,则m的值为( )A、 B、 C、1 D、26. 如图,在平行四边形ABCD中,∠ODA=90°,AC=10,BD=6,则AD的长为( )
3. 由下列条件不能判定 为直角三角形的是( )A、 B、 C、 D、 , ,4. 根式中,最简二次根式有( )A、1个 B、2个 C、3个 D、4个5. 若关于x的函数 是一次函数,则m的值为( )A、 B、 C、1 D、26. 如图,在平行四边形ABCD中,∠ODA=90°,AC=10,BD=6,则AD的长为( )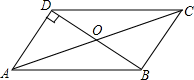 A、4 B、5 C、6 D、87. 某中学规定学生的学期体育成绩满分为100分,其中课外体育占20%,期中考试成绩占30%,期末考试成绩占50%.小彤的这三项成绩(百分制)分别为95分,90分,88分,则小彤这学期的体育成绩为( )A、89分 B、90分 C、92分 D、93分8. 下列四个命题中真命题是( )A、对角线互相垂直平分的四边形是正方形 B、对角线垂直且相等的四边形是菱形 C、对角线相等且互相平分的四边形是矩形 D、四边都相等的四边形是正方形9. 如图,直线y=kx+b交坐标轴于A(﹣2,0),B(0,3)两点,则不等式kx+b>0的解集是( )
A、4 B、5 C、6 D、87. 某中学规定学生的学期体育成绩满分为100分,其中课外体育占20%,期中考试成绩占30%,期末考试成绩占50%.小彤的这三项成绩(百分制)分别为95分,90分,88分,则小彤这学期的体育成绩为( )A、89分 B、90分 C、92分 D、93分8. 下列四个命题中真命题是( )A、对角线互相垂直平分的四边形是正方形 B、对角线垂直且相等的四边形是菱形 C、对角线相等且互相平分的四边形是矩形 D、四边都相等的四边形是正方形9. 如图,直线y=kx+b交坐标轴于A(﹣2,0),B(0,3)两点,则不等式kx+b>0的解集是( )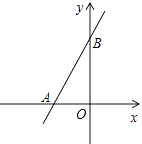 A、x>3 B、﹣2<x<3 C、x<﹣2 D、x>﹣210. 如图,在矩形 中,对角线 与 相交于点 ,若 ,那么 的度数是( )
A、x>3 B、﹣2<x<3 C、x<﹣2 D、x>﹣210. 如图,在矩形 中,对角线 与 相交于点 ,若 ,那么 的度数是( ) A、 B、 C、 D、11. 如图,从一个大正方形中裁去面积为30cm2和48 cm2的两个小正方形,则余下部分的面积为( )
A、 B、 C、 D、11. 如图,从一个大正方形中裁去面积为30cm2和48 cm2的两个小正方形,则余下部分的面积为( )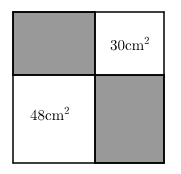 A、78 cm2 B、 cm2 C、 cm2 D、 cm212. 如图,在∠MON的两边上分别截取OA、OB,使OA=OB;分别以点A、B为圆心,OA长为半径作弧,两弧交于点C;连接AC、BC、AB、OC.若AB=2cm,四边形OACB的面积为4cm2 . 则OC的长为( )
A、78 cm2 B、 cm2 C、 cm2 D、 cm212. 如图,在∠MON的两边上分别截取OA、OB,使OA=OB;分别以点A、B为圆心,OA长为半径作弧,两弧交于点C;连接AC、BC、AB、OC.若AB=2cm,四边形OACB的面积为4cm2 . 则OC的长为( )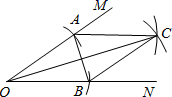 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
13. 实数a在数轴上的位置如图所示,则 化简后为.
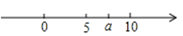 14. 《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为 .15. 如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠CBF为 .
14. 《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为 .15. 如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠CBF为 .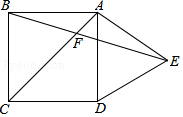 16. 如图,在平面直角坐标系 中,直线 与直线 相交于点 ,则关于 的二元一次方程组 的解是 .
16. 如图,在平面直角坐标系 中,直线 与直线 相交于点 ,则关于 的二元一次方程组 的解是 . 17. 观察下列各式: …请你将发现的规律用含自然数n(n≥1)的等式表示出来 .
17. 观察下列各式: …请你将发现的规律用含自然数n(n≥1)的等式表示出来 .三、解答题
-
18. 计算: .19. 已知a=+2,b=﹣2,求下列代数式的值:a2b+b2a.20. 一次函数的图象与x轴交于点A(1,0),与y轴交于点B(0,-2).
 (1)、一次函数的函数关系式;(2)、若直线AB上有一点C,且△BOC的面积为2,求点C 的坐标;21. 如图,笔直的公路上A、B两点相距25km,C、D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15km,CB=10km,现在要在公路的AB段上建一个土特产品收购站E,使得C、D两村到收购站E的距离相等,则收购站E应建在离A点多远处?
(1)、一次函数的函数关系式;(2)、若直线AB上有一点C,且△BOC的面积为2,求点C 的坐标;21. 如图,笔直的公路上A、B两点相距25km,C、D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15km,CB=10km,现在要在公路的AB段上建一个土特产品收购站E,使得C、D两村到收购站E的距离相等,则收购站E应建在离A点多远处?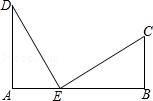 22. 甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
22. 甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图: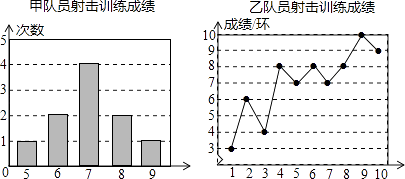
根据以上信息,整理分析数据如下:
平均成绩/环
中位数/环
众数/环
方差
甲
a
7
7
1.2
乙
7
b
8
c
(1)、写出表格中a,b,c的值;(2)、分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?23. 如图,平行四边形ABCD的对角线AC、BD相交于点O,EF过点O且与AB、CD分别相交于点E、F,连接EC.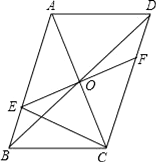 (1)、求证:OE=OF;(2)、若EF⊥AC,△BEC的周长是10,求平行四边形ABCD的周长.24. 某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
(1)、求证:OE=OF;(2)、若EF⊥AC,△BEC的周长是10,求平行四边形ABCD的周长.24. 某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.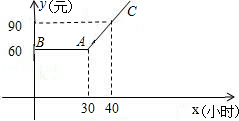 (1)、当x≥30,求y与x之间的函数关系式;(2)、若小李4月份上网20小时,他应付多少元的上网费用?(3)、若小李5月份上网费用为75元,则他在该月份的上网时间是多少?25. 台风是一种自然灾害,它以台风中心为圆心在周围上百千米的范围内形成极端气候,有极强的破坏力,如图,有一台风中心沿东西方向 由 行驶向 ,已知点 为一海港,且点 与直线 上的两点 , 的距离分别为 , ,又 ,以台风中心为圆心周围 以内为受影响区域.
(1)、当x≥30,求y与x之间的函数关系式;(2)、若小李4月份上网20小时,他应付多少元的上网费用?(3)、若小李5月份上网费用为75元,则他在该月份的上网时间是多少?25. 台风是一种自然灾害,它以台风中心为圆心在周围上百千米的范围内形成极端气候,有极强的破坏力,如图,有一台风中心沿东西方向 由 行驶向 ,已知点 为一海港,且点 与直线 上的两点 , 的距离分别为 , ,又 ,以台风中心为圆心周围 以内为受影响区域.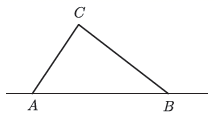 (1)、求 的度数.(2)、海港 受台风影响吗?为什么?(3)、若台风的速度为20千米/小时,当台风运动到点 处时,海港 刚好受到影响,当台风运动到点 时,海港 刚好不受影响,即 ,则台风影响该海港持续的时间有多长?26. 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,垂足为F,交直线MN于E,连接CD,BE.
(1)、求 的度数.(2)、海港 受台风影响吗?为什么?(3)、若台风的速度为20千米/小时,当台风运动到点 处时,海港 刚好受到影响,当台风运动到点 时,海港 刚好不受影响,即 ,则台风影响该海港持续的时间有多长?26. 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,垂足为F,交直线MN于E,连接CD,BE. (1)、求证:CE=AD;(2)、当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;(3)、在满足(2)的条件下,当△ABC满足什么条件时,四边形BECD是正方形?(不必说明理由)
(1)、求证:CE=AD;(2)、当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;(3)、在满足(2)的条件下,当△ABC满足什么条件时,四边形BECD是正方形?(不必说明理由)