内蒙古自治区鄂尔多斯市准格尔旗2020-2021学年八年级下学期期末数学试题

试卷更新日期：2022-04-18 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{0.2}$ B、 $\sqrt{12}$ C、 $\sqrt{3}$ D、 $\sqrt{18}$

查看试题解析
2. 下列计算正确的是（）

A、 $2 \sqrt{3} \times 3 \sqrt{3} = 6 \sqrt{3}$ B、 $\sqrt{2} \div \sqrt{3} = \frac{\sqrt{6}}{3}$ C、 $5 \sqrt{5} - 2 \sqrt{2} = 3 \sqrt{3}$ D、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$

查看试题解析
3. 以下列长度为边长的三角形是直角三角形的是（）

A、5，6，7 B、7，8，9 C、6，8，10 D、5，7，9

查看试题解析
4. 若把一次函数y=2x﹣3的图象向上平移3个单位长度，得到图象对应的函数解析式为（）

A、y=2x B、y=2x﹣6 C、y=4x﹣3 D、y=﹣x﹣3

查看试题解析
5. 下列命题是真命题的是（）

A、有一个角是直角的四边形是矩形 B、对角线互相平分且相等的四边形是矩形 C、一组对边平行且相等的四边形是矩形 D、对角线互相垂直平分的四边形是矩形

查看试题解析
6. 一组数据的方差可以用式子 $s^{2} = \frac{{(x_{1} - 50)}^{2} + {(x_{2} - 50)}^{2} + {(x_{3} - 50)}^{2} + \dots + {(x_{10} - 50)}^{2}}{10}$ 表示，则式子中的数字50所表示的意义是（）

A、这组数据的个数 B、这组数据的平均数 C、这组数据的众数 D、这组数据的中位数

查看试题解析
7. 如图，分别以Rt△ABC的三边为边长向外作等边三角形.若AB＝4，则三个等边三角形的面积之和是（）

A、8 $\sqrt{3}$ B、6 $\sqrt{3}$ C、18 D、12

查看试题解析
8. 如图，菱形ABCD的对角线AC，BD相交于点O，E，F分别是AB，BC边上的中点，连接EF.若 $E F = \sqrt{3}$ ，BD=4，则菱形ABCD的周长为（）

A、4 B、 $4 \sqrt{6}$ C、 $4 \sqrt{7}$ D、28

查看试题解析
9. 如图，在四边形ABCD中，∠DAB=90°，∠DCB=90°，E、F分别是BD、AC的中点，AC=6，BD=10，则EF的长为（）

A、3 B、4 C、5 D、 $\sqrt{7}$

查看试题解析
10. 某公司新产品上市30天全部售完．图1表示产品的市场日销售量与上市时间之间的关系，图2表示单件产品的销售利润与上市时间之间的关系，下列四个结论中不正确的是（　　）

A、第30天该产品的市场日销售量最大 B、第20天至30天该产品的单件产品的销售利润最大 C、第20天该产品的日销售总利润最大 D、第20天至30天该产品的日销售总利润逐日增多

查看试题解析

二、填空题

11. 函数y= $\sqrt{x}$ –1的自变量x的取值范围是.

查看试题解析
12. 在学校的卫生检查中，规定各班的教室卫生成绩占30%，环境卫生成绩占40%，个人卫生成绩占30%．八年级一班这三项成绩分别为85分，90分和95分，求该班卫生检查的总成绩．

查看试题解析
13. 小明从家跑步到学校，接着马上原路步行回家．如图是小明离家的路程y（米）与时间t（分）的关系图象，则小明回家的速度是每分钟步行米．

查看试题解析
14. 若直线 $y = 2 x + b$ 经过直线 $y = x - 2$ 与 $y = - x + 4$ 的交点，则b的值为．

查看试题解析
15. 如图，方格纸中每个最小正方形的边长为l，则两平行直线AB、CD之间的距离是．

查看试题解析
16. 如图，在锐角 $△ A B C$ 中， $A B = \sqrt{2}$ ， $∠ B A C = 45 °$ ， $∠ B A C$ 的平分线交BC于点D，M、N分别是AD和AB上的动点，则 $B M + M N$ 的最小值是．

查看试题解析

三、解答题

17. 计算：

(1)、 ${(\sqrt{2})}^{2} - {(\frac{1}{2})}^{- 1} + \sqrt{8} + {(2 - \sqrt{3})}^{0}$ ；

(2)、 $(\sqrt{50} - \sqrt{18}) \div \sqrt{2} \times \frac{1}{\sqrt{2}}$ ．

查看试题解析
18. 我市自开展“学习新思想，做好接班人”主题阅读活动以来，受到各校的广泛关注和同学们的积极响应，某校为了解全校学生主题阅读的情况，随机抽查了部分学生在某一周主题阅读文章的篇数，并制成统计图表．
某校抽查的学生文章阅读的篇数统计表
文章阅读的篇数/篇
3
4
5
6
7及以上
人数/人
20
28
m
16
12
请根据统计图表中的信息，解答下列问题：

(1)、求被抽查的学生人数和m的值；

(2)、求本次抽查的学生文章阅读篇数的中位数和众数；

(3)、若该校共有800名学生，根据抽查结果，估计该校学生在这一周内文章阅读的篇数为4篇的人数．

查看试题解析
19. 如图1，某商场在一楼到二楼之间设有上、下行自动扶梯和步行楼梯．甲、乙两人从二楼同时下行，甲乘自动扶梯，乙走步行楼梯，甲离一楼地面的高度 $h$ （单位： $m$ ）与下行时间 $x$ （单位： $s$ ）之间具有函数关系 $h = - \frac{3}{10} x + 6$ ，乙离一楼地面的高度 $y$ （单位： $m$ ）与下行时间 $x$ （单位： $s$ ）的函数关系如图2所示．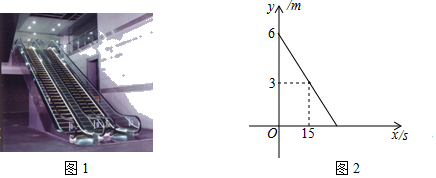

(1)、求 $y$ 关于 $x$ 的函数解析式；

(2)、请通过计算说明甲、乙两人谁先到达一楼地面．

查看试题解析
20. 如图，在△ABC中，AB＝AC，点D为边BC上一点，以AB，BD为邻边作▱ABDE，连接AD、EC.

(1)、求证：△ADC≌△ECD；

(2)、若BD＝CD，求证：四边形ADCE是矩形.

查看试题解析
21. 如图，直线 $l_{1}$ 的解析表达式为 $y = - 3 x + 3$ ，且 $l_{1}$ 与x轴交于点D，直线 $l_{2}$ 经过点A，点B，直线 $l_{1}$ ， $l_{2}$ 交于点C．

(1)、求直线 $l_{2}$ 的解析表达式；

(2)、求 $△ A D C$ 的面积；

(3)、在直线 $l_{2}$ 上存在异于点C的另一点P，使得 $△ A D P$ 的面积等于 $△ A D C$ 面积，请直接写出点P的坐标．

查看试题解析
22. $2021$ 年春，河南某高校为做好新型冠状病毒感染的防治工作，计划为教职工购买一批洗手液（每人 $2$ 瓶）．学校派王老师去商场购买，他在商场了解到，某个牌子的洗手液有两种优惠活动：
活动一：一律打 $9$ 折；
活动二：当购买量不超过 $100$ 瓶时，按原价销售；当购买量超过 $100$ 瓶时，超过的部分打 $8$ 折．
已知所需费用y（元）与购买洗手液的数量x（瓶）之间的函数图象如图所示．

(1)、根据图象可知，洗手液的单价为元/瓶，请直接写出y与x之间的函数关系式；

(2)、请求出a的值；

(3)、如果该高校共有m名教职工，请你帮王老师设计最省钱的购买方案．

查看试题解析
23. 如图，在Rt△ABC中，∠ACB＝90°，过点C的直线MN∥AB，D为AB边上一点，过点D作DE⊥BC，垂足为F，交直线MN于E，连接CD，BE．

(1)、求证：CE＝AD；

(2)、当D为AB中点时，四边形BECD是什么特殊四边形？说明你的理由；

(3)、在满足（2）的条件下，当△ABC满足什么条件时，四边形BECD是正方形？（不必说明理由）

查看试题解析
24. 操作：将一把三角尺放在如图①的正方形 $A B C D$ 中，使它的直角顶点P在对角线 $A C$ 上滑动，直角的一边始终经过点B，另一边与射线 $D C$ 相交于点Q，探究：

(1)、如图②，当点Q在 $D C$ 上时，求证： $P Q = P B$ .

(2)、如图③，当点Q在 $D C$ 延长线上时，①中的结论还成立吗？简要说明理由.

查看试题解析

文章阅读的篇数/篇	3	4	5	6	7及以上
人数/人	20	28	m	16	12