内蒙古自治区包头市固阳县2020-2021学年八年级下学期期末数学试题

试卷更新日期：2022-04-18 类型：期末考试

进入出卷网下载

一、单选题

1. 一次函数y=3x+6的图象经过（）

A、第一、二、三象限 B、第二、三、四象限 C、第一、二、四象限 D、第一、三、四象限

查看试题解析
2. 下列各式正确的是（）

A、 $(\sqrt{a})^{2} = a$ B、 $(\sqrt{a})^{2} = a (a \geq 0)$ C、 $\sqrt{a b} = \sqrt{a} \cdot \sqrt{b}$ D、 $\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} (a \geq 0 ， b \geq 0)$

查看试题解析
3. 在2019年某中学举行的冬季阳径运动会上，参加男子跳高的15名运动员的成绩如表所示：

成绩（m）

1.80

1.50

1.60

1.65

1.70

1.75

人数

1

2

4

3

3

2

这些运动员跳高成绩的中位数和众数分别是（）

A、 $1.70 m, 1.65 m$ B、 $1.70 m ， 1.70 m$ C、 $1.65 m ， 1.65 m$ D、 $1.65 m ， 1.60 m$

查看试题解析
4. 四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（）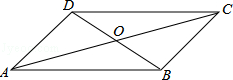

A、AB//DC，AD//BC B、AB=DC，AD=BC C、AO=CO，BO=DO D、AB//DC，AD=BC

查看试题解析
5. 如图，Rt△ABC中，∠ACB＝90°，以Rt△ABC的三边为边向外作正方形，其面积分别为S₁ ， S₂ ， S₃ ，且，且S₁＝4，S₃＝16，则S₂＝（）

A、20 B、12 C、2 $\sqrt{5}$ D、2 $\sqrt{3}$

查看试题解析
6. 如图，矩形ABCD中，AB=7，BC=4，按以下步骤作图：以点B为圆心，适当长为半径画弧，交AB，BC于点E，F；再分别以点E，F为圆心，大于 $\frac{1}{2}$ EF的长为半径画弧，两弧在∠ABC内部相交于点H，作射线BH，交DC于点G，则DG的长为（）

A、1 B、1 $\frac{1}{2}$ C、3 D、2 $\frac{1}{2}$

查看试题解析
7. 点 $P (x ， y)$ 在第一象限，且 $x + y = 8$ ，点A的坐标为 $(6 ， 0)$ ，若 $△ O P A$ 的面积为12，则点P的坐标为（）

A、 $(2 ， 6)$ B、 $(4 ， 4)$ C、 $(6 ， 2)$ D、 $(12 ， - 4)$

查看试题解析
8. 在如图的网格中，每个小正方形的边长为1，A、B、C三点均在正方形格点上，若 $A D$ 是 $△ A B C$ 的高，则 $A D$ 的长为（）

A、 $2 \sqrt{3}$ B、 $\sqrt{5}$ C、 $\sqrt{3}$ D、2

查看试题解析
9. 如图，平行四边形 $A B C D$ 的周长为20，对角线 $A C$ ， $B D$ 相交于点O．点E是 $C D$ 的中点， $B D = 6$ ，则 $△ D O E$ 的周长为（）

A、6 B、7 C、8 D、10

查看试题解析
10. 下列4个命题：
①对角线相等且互相平分的四边形是正方形；②有三个角是直角的四边形是矩形；③对角线互相垂直的平行四边形是菱形；④一组对边平行，另一组对边相等的四边形是平行四边形其中正确的是（）

A、②③ B、② C、①②④ D、③④

查看试题解析
11. 如图，菱形ABCD中，对角线AC＝6，BD＝8，M、N分别是BC、CD上的动点，P是线段BD上的一个动点，则PM＋PN的最小值是（）

A、 $\frac{9}{5}$ B、 $\frac{12}{5}$ C、 $\frac{16}{5}$ D、 $\frac{24}{5}$

查看试题解析
12. 如图，正方形纸片ABCD中，对角线AC、BD交于点O ，折叠正方形纸片ABCD ，使AD落在BD上，点A恰好与BD上的点F重合，展开后折痕 DE分别交AB、AC于点E、G ，连结GF ，给出下列结论：① $∠ A D G = 22.5 °$ ；② $\frac{A D}{A E} = 2$ ；③ $S_{△ A G D} = S_{△ O G D}$ ；④四边形 AEFG是菱形；⑤ $B E = 2 O G$ ；⑥若 $S_{△ O G F} = 1$ ，则正方形 ABCD的面积是 $6 + 4 \sqrt{2}$ ，其中正确的结论个数为（）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

13. 已知 $x ， y$ 是实数，且满足 $y = \sqrt{x - 2} + \sqrt{2 - x} + 12$ ，则xy的平方根是．

查看试题解析
14. 若一个三角形的三边之比为5：12：13，且周长为60cm，则它的面积为cm² ．

查看试题解析
15. 若函数y＝x^m+1+1是一次函数，则常数m的值是．

查看试题解析
16. 甲、乙两人在相同条件下各射击10次，他们的成绩平均数相同，方差分别是 $S_{甲}^{2} = 0.34$ ， $S_{乙}^{2} = 0.26$ ，则射击成绩较稳定的是（填“甲”或“乙”）．

查看试题解析
17. 已知一次函数 $y = - 2 x + 1$ ，若 $- 2 \leq x \leq 1$ ，则y的最小值为.

查看试题解析
18. 如图，点E为正方形ABCD边CB延长线上一点，点F为AB上一点，连接AE，CF，AC，若BE=BF，∠E=70°，则∠ACF= ．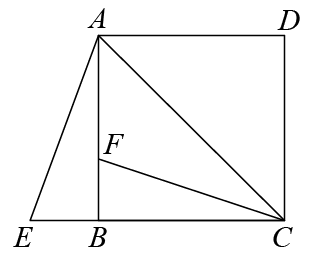

查看试题解析
19. 菱形ABCD的对角线AC ， BD相交于点O ， E是AD的中点，点F ， G在AB上，EF⊥AB ， OG∥EF ． AD=10，EF=4，则BG的长．

查看试题解析
20. 如图，矩形 $A B C D$ 中， $A B = 6 ， B C = 8$ ，点E是 $B C$ 边上一点，连接 $A E$ ，把 $△ A B E$ 沿 $A E$ 折叠，使点B落在点F处，当 $△ C E F$ 为直角三角形时， $C F$ 的长为.

查看试题解析

三、解答题

21. 计算：

(1)、 ${(2 \sqrt{2} - 1)}^{2} + (\sqrt{2} + 2) (\sqrt{2} - 2)$

(2)、 $\sqrt{4} - \frac{\sqrt{27} - \sqrt{12}}{\sqrt{3}}$

查看试题解析
22. 南浦实验中学某班级需要选出1名同学去参加校品学兼优生的竞选，现A，B，C，D，E，5名候选人还需过2轮评选．
第一轮：由全班50位同学匿名投票，每人选2名同学（不弃权，不重复），挑选出票数最高的2位同学．已知5位候选人的得票数如图
第二轮：根据行规、学规、任课老师打分3个角度综合分析评选，两位同学的情况如表
候选人
A
C
行规
110
105
学规
110
112
任课老师打分
85
88

(1)、第一轮5位候选人票数的中位数是票；

(2)、如果学校认为这三个项目重要程度有所不同．而给予“行规”“学规”“任课老师”三个项目在总分中所占的比例分别为 $40 % ， 30 % ， 30 %$ ，那么通过排序后最后进入校品学兼优生竞选的是哪位同学？请说明理由．

查看试题解析
23. 如图，四边形 $A C F D$ 是平行四边形，B，E，C，F在一条直线上，已知 $B E = C F$ ．

(1)、求证：四边形 $A B E D$ 是平行四边形．

(2)、若 $∠ A B C = 60 °$ ，且 $A C ⊥ B F$ ， $A B = 6$ ， $B F = 5$ ，求 $A D$ 的长．

查看试题解析
24. 某市为改善农村生活条件，满足居民清洁能源的需求，计划修建A、B两种型号的沼气池共24个，两种沼气池的修建费用、可供使用户数、占地面积如表：
沼气池
修建费用（万元/个）
可供使用户数（户/个）
占地面积（平方米/个）
A型
3
20
10
B型
2
15
8
设修建A型沼气池x个，修建两种沼气池共需费用y万元．

(1)、求y与x之间的函数关系式；

(2)、若此次修建沼气池至少要保证幸福村400户的居民每户一个，且政府土地部门只批给该村沼气池用地220平方米，求出费用最少时的修建方案，并计算此时修建完沼气池剩余的用地面积．

查看试题解析
25. 如图，直线l：y＝﹣ $\frac{1}{2}$ x+2与x轴，y轴分别交于A，B两点，在y轴上有一点C（0，4），动点M从点A出发以每秒1个单位的速度沿x轴向左移动．

(1)、求A，B两点的坐标；

(2)、求△COM的面积S与点M的移动时间t之间的函数关系式；

(3)、当t＝6时，
①直接写出直线CM所对应的函数表达式；

②问直线CM与直线 $l$ 有怎样的位置关系？请说明理由．

查看试题解析
26. 在菱形 $A B C D$ 中， $∠ A B C = 60 °$ ，点 $P$ 是射线 $B D$ 上一动点，以 $A P$ 为边向右侧作等边 $△ A P E$ ．
（1）如图1，当点E在菱形 $A B C D$ 内部或边上时，连接 $C E ， B P$ 与 $C E$ 的数量关系是____， $C E$ 与 $A D$ 的位置关系是____；

(1)、当点E在菱形 $A B C D$ 外部时（1）中的结论是否还成立？若成立，请予以证明；若不成立，请说明理由．（请结合图2的情况予以证明或说理．）

(2)、如图3，当点P在线段 $B D$ 的延长线上时，连接 $B E$ ，若 $A B = 2 ， B E = \sqrt{31}$ ，求四边形 $A D P E$ 的面积．

查看试题解析

沼气池	修建费用（万元/个）	可供使用户数（户/个）	占地面积（平方米/个）
A型	3	20	10
B型	2	15	8

成绩（m）	1.80	1.50	1.60	1.65	1.70	1.75
人数	1	2	4	3	3	2

候选人	A	C
行规	110	105
学规	110	112
任课老师打分	85	88