内蒙古科尔沁左翼中旗2020-2021学年八年级下学期期末考试数学试题
试卷更新日期:2022-04-18 类型:期末考试
一、单选题
-
1. 最简二次根式与最简二次根式是同类二次根式,则x的值为( )A、 B、 C、 D、2. 以下列几组数为三角形的边,能组成直角三角形的是( )A、5、10、12 B、6、8、10 C、2、3、4 D、4、5、63. 若=6-x,则x的取值范围是( )A、x<6 B、x≤6 C、x≥6 D、x≠64. 一次函数y=x+2的图象不经过()A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 下列命题中,不正确的是( )A、矩形的对角线互相平分且相等 B、菱形的两条对角线相等 C、菱形的面积等于对角线乘积的一半 D、正方形的对角线相等且互相垂直平分6. 在正方形中, , , , 则点E、F之间的距离是( )
 A、 B、 C、5 D、67. 如图,对四边形增加条件,使之成为平行四边形,下面添加不正确的是( )
A、 B、 C、5 D、67. 如图,对四边形增加条件,使之成为平行四边形,下面添加不正确的是( ) A、 B、 C、 D、与相互平分8. 2016年,某市发生了严重干旱,该市政府号召居民节约用水,为了解居民用水情况,在某小区随机抽查了10户家庭的月用水量,结果统计如图,则关于这10户家庭的月用水量,下列说法不正确的是( )
A、 B、 C、 D、与相互平分8. 2016年,某市发生了严重干旱,该市政府号召居民节约用水,为了解居民用水情况,在某小区随机抽查了10户家庭的月用水量,结果统计如图,则关于这10户家庭的月用水量,下列说法不正确的是( ) A、众数是6 B、中位数是6 C、平均数是6 D、方差是49. 甲、乙两地高速铁路建设成功,一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车均匀速行驶并同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系,下列说法:
A、众数是6 B、中位数是6 C、平均数是6 D、方差是49. 甲、乙两地高速铁路建设成功,一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车均匀速行驶并同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系,下列说法:①甲、乙两地相距1800千米;
②点B的实际意义是两车出发后4小时相遇;
③m=6,n=900;
④动车的速度是450千米/小时.
其中不正确的是( )
 A、① B、② C、③ D、④10. 如图,点O为平面直角坐标系的原点,点A在x轴正半轴上,四边形OABC是菱形.已知点B坐标为(3, ),则直线AC的函数解析式为( )
A、① B、② C、③ D、④10. 如图,点O为平面直角坐标系的原点,点A在x轴正半轴上,四边形OABC是菱形.已知点B坐标为(3, ),则直线AC的函数解析式为( ) A、y= x+ B、y= x+2 C、y=﹣ x+ D、y=﹣ x+2
A、y= x+ B、y= x+2 C、y=﹣ x+ D、y=﹣ x+2二、填空题
-
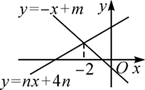
11. 一次函数的图象经过点 , 那么k= .12. 如图,直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m>nx+4n的解集为 .
 13. 如图,有一块菱形纸片ABCD,沿高DE剪下后拼成一个矩形,矩形的长和宽分别是5cm,3cm.EB的长是.
13. 如图,有一块菱形纸片ABCD,沿高DE剪下后拼成一个矩形,矩形的长和宽分别是5cm,3cm.EB的长是. 14. 某小组七位学生的中考体育测试成绩(满分40分)依次为37,40,39,37,40,38,40.则这组数据的中位数是 .15. 平行四边形中,对角线、交于点O,点E是的中点.若 , 则的长为 .16. 对于任意不相等的两个实数 , ,新定义一种运算“※”如下: ※ ,则2※ .17. 如图所示,矩形中, , , 点M在边上,若平分 , 则的长是 .
14. 某小组七位学生的中考体育测试成绩(满分40分)依次为37,40,39,37,40,38,40.则这组数据的中位数是 .15. 平行四边形中,对角线、交于点O,点E是的中点.若 , 则的长为 .16. 对于任意不相等的两个实数 , ,新定义一种运算“※”如下: ※ ,则2※ .17. 如图所示,矩形中, , , 点M在边上,若平分 , 则的长是 .
三、解答题
-
18. 计算(1)、(2)、19. 已知: , 求代数式的值.20. 已知函数y=(m+1)x2-|m|+n+4.(1)、当m,n为何值时,此函数是一次函数?(2)、当m,n为何值时,此函数是正比例函数?21. 某学校为了了解本校1200名学生的课外阅读的情况,现从各年级随机抽取了部分学生,对他们一周的课外阅读时间进行了调整,井绘制出如下的统计图①和图②,根据相关信息,解答下列问题:
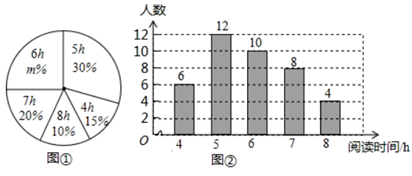 (1)、本次接受随机抽样调查的学生人数为 , 图①中 的值为;(2)、求本次调查获取的样本数据的众数、中位数和平均数;(3)、根据样本数据,估计该校一周的课外阅读时间大于 的学生人数.22. 如图所示,小明制作一个模具, , , , , , 求这个模具的面积.
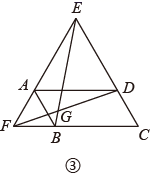
(1)、本次接受随机抽样调查的学生人数为 , 图①中 的值为;(2)、求本次调查获取的样本数据的众数、中位数和平均数;(3)、根据样本数据,估计该校一周的课外阅读时间大于 的学生人数.22. 如图所示,小明制作一个模具, , , , , , 求这个模具的面积. 23. 如图,在平行四边形ABCD中,点E是边AD的中点,连接CE并延长交BA的延长线于点F,连接AC,DF.
23. 如图,在平行四边形ABCD中,点E是边AD的中点,连接CE并延长交BA的延长线于点F,连接AC,DF. (1)、求证: AEF≌ DEC;(2)、求证:四边形ACDF是平行四边形.24. 为加快复工复产,某企业需运输批物资.据调查得知,2辆大货车与3辆小货车一次可以运输600箱;5辆大货车与6辆小货车一次可以运输1350箱.(1)、求1辆大货车和1辆小货车一次可以分别运输多少箱物资;(2)、计划用两种货车共12辆运输这批物资,每辆大货车一次需费用5 000元,每辆小货车一次需费用3000元.若运输物资不少于1500箱,且总费用小于54000元,请你列出所有运输方案,并指出哪种方案所需费用最少,最少费用是多少?
(1)、求证: AEF≌ DEC;(2)、求证:四边形ACDF是平行四边形.24. 为加快复工复产,某企业需运输批物资.据调查得知,2辆大货车与3辆小货车一次可以运输600箱;5辆大货车与6辆小货车一次可以运输1350箱.(1)、求1辆大货车和1辆小货车一次可以分别运输多少箱物资;(2)、计划用两种货车共12辆运输这批物资,每辆大货车一次需费用5 000元,每辆小货车一次需费用3000元.若运输物资不少于1500箱,且总费用小于54000元,请你列出所有运输方案,并指出哪种方案所需费用最少,最少费用是多少?