内蒙古呼和浩特市2020-2021学年八年级下学期期末考试数学试题
试卷更新日期:2022-04-18 类型:期末考试
一、单选题
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 下列各式中,化简后不能与 合并的是( )A、 B、 C、 D、3. 已知为的内角所对应的边,满足下列条件的三角形不是直角三角形的是( )A、 B、 C、 D、4. 均匀地向一个容器注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为一折线),则这个容器的形状为( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 自去年9月《北京市打赢蓝天保卫战三年行动计划》发布以来,北京市空气质量呈现“优增劣减”特征,“蓝天”含金量进一步提高,下图是今年5月17日至31日的空气质量指数趋势图.
5. 自去年9月《北京市打赢蓝天保卫战三年行动计划》发布以来,北京市空气质量呈现“优增劣减”特征,“蓝天”含金量进一步提高,下图是今年5月17日至31日的空气质量指数趋势图.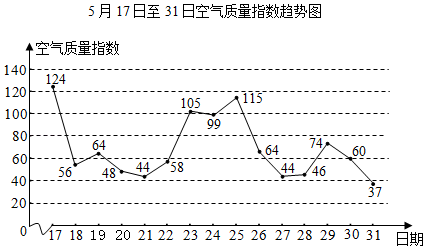
(说明:空气质量指数为0﹣50、51﹣100、101﹣150分别表示空气质量为优、良、轻度污染)有如下结论:①在此次统计中,空气质量为优良的天数占;②在此次统计中,空气质量为优的天数多于轻度污染的天数;③20,21,22三日的空气质量指数的方差小于26,27,28三日的空气质量指数的方差.所有正确结论的序号是( )
A、① B、①② C、②③ D、①②③6. 下列说法正确的是( )A、一组对边平行另一组对边相等的四边形是平行四边形 B、对角线相等的四边形是矩形 C、对角线互相垂直且相等的四边形是正方形 D、如果顺次连接四边形的各边中点得到的四边形是菱形,那么原来四边形的对角线一定相等7. 如图,一次函数y=mx+n与正比例函数y=mnx(m,n为常数,且mn≠0,n>0)的图象是( )A、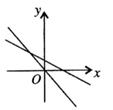 B、
B、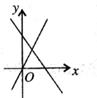 C、
C、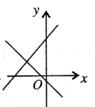 D、
D、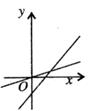 8. 如图,已知正方形ABCD的边长为4,P是对角线BD上一点,于点E,于点F,连接AP,给出下列结论:①;②四边形PECF的周长为8;③一定是等腰三角形;④;⑤EF的最小值为;其中正确结论的序号为( )
8. 如图,已知正方形ABCD的边长为4,P是对角线BD上一点,于点E,于点F,连接AP,给出下列结论:①;②四边形PECF的周长为8;③一定是等腰三角形;④;⑤EF的最小值为;其中正确结论的序号为( ) A、①②④ B、①③⑤ C、②③④ D、①②④⑤
A、①②④ B、①③⑤ C、②③④ D、①②④⑤二、填空题
-
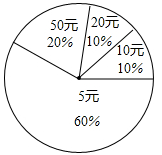
9. 二次根式 在实数范围内有意义,x的取值范围是.10. 在一次爱心捐款中,某班有40名学生拿出自己的零花钱,有捐5元、10元、20元、50元的.如图反映了不同捐款的人数比例,那么这个班的学生平均每人捐款元
 11. 在中,AE平分 , 交CD边于E, , , 则的周长为 .12. 若菱形的周长为20cm,一个内角为60°,则菱形的面积为 .13. 已知一次函数 , y随x的增大而减小,且图像交于x的正半轴,则k的取值范围是 .14. 如图是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若 , ,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图所示的“数学风车”,则这个风车的外围周长是 .
11. 在中,AE平分 , 交CD边于E, , , 则的周长为 .12. 若菱形的周长为20cm,一个内角为60°,则菱形的面积为 .13. 已知一次函数 , y随x的增大而减小,且图像交于x的正半轴,则k的取值范围是 .14. 如图是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若 , ,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图所示的“数学风车”,则这个风车的外围周长是 .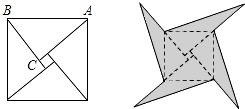 15. 在矩形ABCD中,已知两条邻边AB与BC的长分别为2和3,若M是边CD的中点,连接AM,过点B作 , 垂足为点H,则BH的长 .16. 已知一次函数(k、b为常数,且 , )与的图象相交于点 , 则关于x的方程的解为 .
15. 在矩形ABCD中,已知两条邻边AB与BC的长分别为2和3,若M是边CD的中点,连接AM,过点B作 , 垂足为点H,则BH的长 .16. 已知一次函数(k、b为常数,且 , )与的图象相交于点 , 则关于x的方程的解为 .三、解答题
-
17. 化简与计算(1)、(2)、18. 已知一次函数 的图象经过点 且与正比例函数 的图象相交于点 ,求:
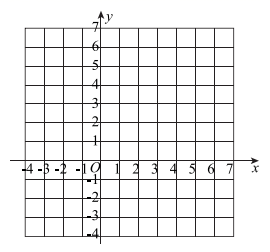 (1)、a的值;(2)、求一次函数 的表达式;(3)、请你画出这两个函数的图象,并判断当 取何值时, ;(4)、求这两个函数图象与 轴围成的三角形的面积.19. 如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=CD,连接CF.
(1)、a的值;(2)、求一次函数 的表达式;(3)、请你画出这两个函数的图象,并判断当 取何值时, ;(4)、求这两个函数图象与 轴围成的三角形的面积.19. 如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=CD,连接CF. (1)、求证:△AEF≌△DEB;(2)、若AB=AC,试判断四边形ADCF的形状,并证明你的结论.20. 某书定价a元,如果一次购买10本以上.超过10本部分打8折,下面用列表法表达了购买书的数量和付款金额这两个变量的对应关系.
(1)、求证:△AEF≌△DEB;(2)、若AB=AC,试判断四边形ADCF的形状,并证明你的结论.20. 某书定价a元,如果一次购买10本以上.超过10本部分打8折,下面用列表法表达了购买书的数量和付款金额这两个变量的对应关系.购买书数量(本)
1
5
10
15
20
付款金额(元)
a
40
80
112
b
(1)、请直接写出上表中a,b的值.(2)、请用解析法求出购买书数量与付款金额之间的函数关系.(3)、小强一次购买书恰好花了92元8角,小华购买了8本书,分别计算他们的购买书量和付款金额.21. 如图,四边形 是菱形,点H为对角线 的中点,点E在 的延长线上, ,垂足为E,点F在 的延长线上, ,垂足为F.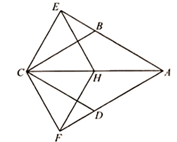 (1)、若 ,求证:四边形 是菱形;(2)、若 , 的面积为16,求菱形 的面积.22. 2020年是不平凡的一年,新年伊始,一场突如其来的疫情席卷全国,全国人民万众一心,抗战疫情.为了早日取得抗疫的胜利,各级政府、各大新闻媒体都加大了对防疫知识的宣传.某校为了解初一年级共480名学生对防疫知识的掌握情况,对他们进行了防疫知识测试.现随机抽取甲、乙两班各15名同学的测试成绩(满分100)进行整理分析,过程如下:
(1)、若 ,求证:四边形 是菱形;(2)、若 , 的面积为16,求菱形 的面积.22. 2020年是不平凡的一年,新年伊始,一场突如其来的疫情席卷全国,全国人民万众一心,抗战疫情.为了早日取得抗疫的胜利,各级政府、各大新闻媒体都加大了对防疫知识的宣传.某校为了解初一年级共480名学生对防疫知识的掌握情况,对他们进行了防疫知识测试.现随机抽取甲、乙两班各15名同学的测试成绩(满分100)进行整理分析,过程如下:收集数据:
甲班15名学生测试成绩分别如下:79,84,89,97,98,85,99,94,87,90,93,92,99,95,99
乙班15名学生测试成绩中的成绩如下:91,92,94,90,93
整理数据:
班级
甲
1
1
3
4
a
乙
1
2
3
5
4
分析数据:
班级
平均数
中位数
众数
方差
甲
92
93
c
36.1
乙
90
b
87
40.2
根据以上信息,回答下列问题
(1)、a=;b=;c=;(2)、若规定测试成绩92分及以上为优秀,请估计参加防疫知识测试的480名学生中成绩为优秀的学生共有多少人;(3)、根据以上数据,你认为哪个班的学生防疫测试的整体成绩较好?请说明理由至少从两个不同的角度说明推断的合理性.23. 已知某酒店的三人间和双人间客房标价为:三人间为每人每天200元,双人间为每人每天300元,为吸引客源,促进旅游,在“十·一”黄金周期间酒店进行优惠大酬宾,凡团体入住一律五折优惠.一个50人的旅游团在十月二号到该酒店住宿,租住了一些三人间、双人间客房.(1)、如果租住的每个客房正好住满,并且一天一共花去住宿费6300元.求租住了三人间、双人间客房各多少间?(2)、设三人间共住了 人,这个团一天一共花去住宿费 元,请写出 与 的函数关系式,并写出自变量的取值范围.(3)、一天6300元的住宿费是否为最低?如果不是,请设计一种方案:要求租住的房间正好被住满的,并使住宿费用最低,请写出设计方案,并求出最低的费用.