辽宁省沈阳市沈河区2020-2021学年八年级下学期期末数学试题

试卷更新日期：2022-04-18 类型：期末考试

进入出卷网下载

一、单选题

1. 如果 $x < y$ ，那么下列不等式正确的是（）

A、 $2 x < 2 y$ B、 $- 2 x < - 2 y$ C、 $x - 1 > y - 1$ D、 $x + 1 > y + 1$

查看试题解析
2. 若分式 $\frac{x^{2} - 4}{x + 2}$ 的值为0，则x的值为（）

A、-2 B、0 C、2 D、±2

查看试题解析
3. 下列垃圾分类标识中，是中心对称图形的是（　　　）

A、 B、 C、 D、

查看试题解析
4. 如图，在平行四边形ABCD中，∠A＝40°，则∠C大小为（）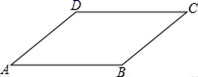

A、40° B、80° C、140° D、180°

查看试题解析
5. 下列各式从左到右的变形一定正确的是（）

A、 $\frac{n}{m}$ ＝ $\frac{n + 1}{m + 1}$ B、 $\frac{x^{2} - y^{2}}{x - y}$ ＝x﹣y C、 $\frac{b}{a}$ ＝ $\frac{b^{2}}{a^{2}}$ D、 $\frac{b}{a}$ ＝ $\frac{a b}{a^{2}}$

查看试题解析
6. 下列多项式能直接用完全平方公式进行因式分解的是（）

A、x²+2x﹣1 B、x²﹣x+ $\frac{1}{4}$ C、x²+xy+y² D、9+x²﹣3x

查看试题解析
7. 下列命题不正确的是（）

A、等腰三角形的两底角相等 B、平行四边形的对角线互相平分 C、角平分线上的点到角两边的距离相等 D、三个角分别对应相等的两个三角形全等

查看试题解析
8. 下列条件不能判定四边形 $A B C D$ 是平行四边形的是（）.

A、 $A D = B C$ ， $A B = C D$ B、 $∠ A = ∠ C$ ， $∠ B = ∠ D$ C、 $A B / / C D$ ， $B C = A D$ D、 $A D / / B C$ ， $∠ B = ∠ D$

查看试题解析
9. 如图，一次函数 $y_{1} = k x + b$ 的图象与直线 $y_{2} = m$ 相交于点 $P$ （-1，3），则关于 $x$ 的不等式 $k x + b - m > 0$ 的解集为（）

A、 $x > 3$ B、 $x < - 1$ C、 $x > - 1$ D、 $x < 3$

查看试题解析
10. 如图，已知∠ABC，小彬借助一把没有刻度且等宽的直尺，按如图的方法画出了∠ABC的平分线BP．他这样做的依据是（）

A、在一个角的内部，且到角两边的距离相等的点在这个角的平分线上 B、角平分线上的点到这个角两边的距离相等 C、三角形三条角平分线的交点到三条边的距离相等 D、测量垂直平分线上的点到这条线段的距离相等

查看试题解析

二、填空题

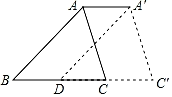
11. 已知一个多边形的每个外角都是30°，那么这个多边形的边数是．

查看试题解析
12. 如图，在△ABC中，BC＝8cm，D是BC的中点，将△ABC沿BC向右平移得△A′DC′，则点A平移的距离AA′＝cm.

查看试题解析
13. 计算： $\frac{a^{2} + 3}{a^{2} - 1} - \frac{2}{a - 1} =$ ．

查看试题解析
14. 实验初中初二（1）班同学参加社会实践活动，几名同学打算包租一辆车前往，该车的租价为180元，出发时，又增加了两名同学，结果每名同学比原来少分摊了3元车费．设参加实践活动的学生原有x人，则可列方程为．

查看试题解析
15. 如图，四边形ABCD中，∠B＋∠D＝180°，AC平分∠DAB，CM⊥AB于点M，若AM＝4cm，BC＝2.5cm，则四边形ABCD的周长为cm．

查看试题解析
16. 如图，▱ABCD中，∠ABC＝45°，EF是BC的垂直平分线，EB＝AB，若BD＝6，则AB＝．

查看试题解析

三、解答题

17. 分解因式：

(1)、 $2 x^{2} - 4 x + 2$

(2)、 $a^{2} (x - y) + 9 b^{2} (y - x)$

查看试题解析
18. 利用数轴求出不等式组的解集． ${\begin{array}{l} 3 x < x + 2 \\ \frac{x + 1}{2} > \frac{2 x + 1}{5} \end{array}$ ．

查看试题解析
19. 先化简：（ $\frac{a + 7}{a - 1} - \frac{2}{a + 1}$ ）÷ $\frac{a^{2} + 3 a}{a^{2} - 1}$ ，再从﹣3、﹣2、﹣1、0、1中选一个合适的数作为a的值代入求值.

查看试题解析
20. 解分式方程： $\frac{x}{x + 1} - 1 = \frac{2 x}{3 x + 3}$

查看试题解析
21. 如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣3，5），B（﹣2，1），C（﹣1，3）．

(1)、若△ABC经过平移后得到△A₁B₁C₁ ，已知点C₁的坐标为（4，0），画出△A₁B₁C₁；

(2)、将△ABC绕着点O按顺时针方向旋转90°得到△A₂B₂C₂ ，则点A₂的坐标为，点C₂的坐标为．

(3)、点D是平面直角坐标系内一点，若以A、B、C、D为顶点的四边形为平行四边形，直接写出满足条件的D点坐标．

查看试题解析
22. 如图，在▱ABCD中，对角线AC、BD相交于点O，E、F为直线BD上的两个动点（点E、F始终在▱ABCD的外面），且DE＝ $\frac{1}{2}$ OD，BF＝ $\frac{1}{2}$ OB，连接AE、CE、CF、AF．

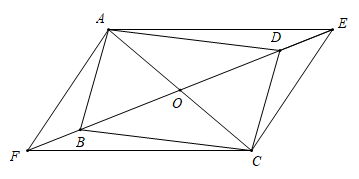(1)、求证：四边形AFCE为平行四边形．

(2)、若AC＝6，EF＝10，AF＝4，则平行四边形AFCE的周长为．

查看试题解析
23. 某网店预测一种时尚T恤衫能畅销，用4800元购进这种T恤衫，很快售完，接着又用6600元购进第二批这种T恤衫，第二批T恤衫数量是第一批T恤衫数量的1.5倍，且每件T恤衫的进价第二批比第一批的少5元．

(1)、求第一批T恤衫每件的进价是多少元？

(2)、若第一批T恤衫的售价是80元/件，老板想让这两批T恤衫售完后的总利润不低于4060元，则第二批T恤衫每件至少要售多少元？（T恤衫的售价为整数元）

查看试题解析
24. 如图，在四边形ABCD中，∠B＝60°，AB＝DC＝4，AD＝BC＝8，延长BC到E，使CE＝4，连接DE，动点P从点B出发，以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动，设点P运动的时间为t秒(t＞0)．

(1)、当t＝3时，BP＝；

(2)、当t＝时，点P运动到∠B的角平分线上；

(3)、当0＜t＜6时，请用含t的代数式表示△ABP的面积S；

(4)、当0＜t＜6时，直接写出点P到四边形ABED相邻两边距离相等时t的值．

查看试题解析
25. 如图

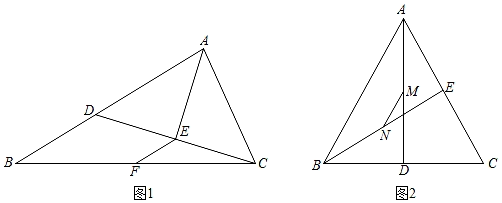(1)、思维启迪
如图，△ABC中，AB＝4，AC＝2，点在AB上，AD＝AC，AE⊥CD垂足为E，点F是BC中点，则EF的长度为．

(2)、思维探索
如图2，等边三角形ABC的边长为4，AD⊥BC垂足为D，点E是AC的中点，点M是AD的中点，点N是BE的中点，求MN的长．

(3)、将（2）中的△CDE绕C点旋转，其他条件不变，当点D落在直线AC上时，画出图形，并直接写出MN长．

查看试题解析