辽宁省沈阳市和平区2020-2021学年八年级下学期期末数学试题

试卷更新日期：2022-04-18 类型：期末考试

进入出卷网下载

一、单选题

1. 若分式 $\frac{x - 1}{x + 1}$ 无意义，则x的取值范围是（　　）

A、x＝1 B、x＝﹣1 C、x≠﹣1 D、x≠1且x≠﹣1

查看试题解析
2. 如图，一个圆柱体在正方体上沿虚线从左向右平移，平移过程中不变的是（　　）

A、主视图 B、俯视图 C、左视图 D、主视图和左视图

查看试题解析
3. 下列四个图形中，不是轴对称图形，是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
4. 如图，点O在 $△ A B C$ 内，且到三边的距离相等，∠A＝64°，则∠BOC的度数为（）

A、58° B、64° C、122° D、124°

查看试题解析
5. 已知，四边形ABCD是平行四边形，下列结论中不正确的是（　　）

A、当BC＝CD时，它是菱形 B、当AC⊥BD时，它是菱形 C、当∠ABC＝90°时，它是矩形 D、当AC＝BD时，它是正方形

查看试题解析
6. 不等式组 ${\begin{array}{l} x - 4 > 3 (x - 2) \\ 3 x \geq 2 x - 1 \end{array}$ 的解集在数轴上表示正确的是（　　）

A、 B、 C、 D、

查看试题解析
7. 在 $△$ ABC中，若AB＝10，AC＝15，∠BAC＝150°，则 $△$ ABC的面积为（　　）

A、37.5 B、75 C、100 D、150

查看试题解析
8. 若x²-kx+9是一个完全平方式，那么k的值是（）

A、3 B、±3 C、6 D、±6

查看试题解析
9. 如图，剪两张对边平行的纸片随意交叉叠放在一起，转动其中一张，重合部分构成一个四边形，则下列结论中不一定成立的是（　　）

A、∠ABC+∠BCD＝180° B、∠ABC＝∠ADC C、AB＝CD D、AB＝BC

查看试题解析
10. 如图，正四棱柱的底面边长为10cm，侧棱长为16cm，一只蚂蚁从点A出发，沿棱柱侧面到点C′处吃食物，那么它需要爬行的最短路径的长是（　　）cm

A、8 $\sqrt{41}$ B、4 $\sqrt{41}$ C、2 $\sqrt{41}$ D、12

查看试题解析

二、填空题

11. 分解因式：x²﹣x= ．

查看试题解析
12. 若一个多边形外角和与内角和相等，则这个多边形是.

查看试题解析
13. 如图，△ODC是由△OAB绕点O顺时针旋转30°后得到的图形，若点D恰好落在AB上，且∠AOC的度数为100°，则∠C的度数是．

查看试题解析
14. 若关于x的方程 $\frac{2 x + m}{x - 1}$ ＝3的解为非负数，则m的取值范围是．

查看试题解析
15. 如图，点O是矩形ABCD的对角线AC的中点，M是AD的中点，若OM=3，BC=8，则OB的长为。

查看试题解析
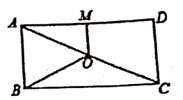16. 如图，在 $△$ ABC中，∠ACB＝45°，AD⊥BC，BE⊥AC，AD与BE相交于点F，连接并延长CF交AB于点G，∠AEB的平分线交CG的延长线于点H，连接AH，则下列结论：①∠EBD＝45°；②AH＝HF；③ $△$ ABD≌ $△$ CFD；④CH＝AB+AH；⑤BD＝CD﹣AF．其中正确的是．（只填写序号）

查看试题解析

三、解答题

17. 分解因式：（2m+3）²﹣m² ．

查看试题解析
18. 先化简，再求值： $\frac{m^{2} + m}{m^{2} + 2 m + 1}$ ÷（ $\frac{1}{m} - \frac{1}{m + 1}$ ），其中m＝﹣2．

查看试题解析
19. 如图，在 $△ A B C$ 中，AB＝AC，AB的垂直平分线MN交AC于点D，交AB于点E．

(1)、若∠C＝70°，求∠DBC的度数；

(2)、若BE＝3， $△ A B C$ 的周长为16，直接写出 $△ C B D$ 的周长为．

查看试题解析
20. 如图，在平面直角坐标系中，点A（﹣1，3），B（﹣4，1），C（﹣2，1），先将 $△$ ABC沿一确定方向平移得到 $△$ A₁B₁C₁（点A的对应点为点A₁ ，点B的对应点为点B₁ ，点C的对应点为点C₁），点A₁的坐标是（0，2），再将 $△$ A₁B₁C₁绕原点O顺时针旋转90°得到 $△$ A₂B₂C₂（点A₁的对应点为点A₂ ，点B₁的对应点为点B₂ ，点C₁的对应点为点C₂）．
⑴先画出 $△$ A₁B₁C₁；
⑵再画出 $△$ A₂B₂C₂；
⑶若点D为平面内一点，请直接写出以A₂ ， B₂、C₂为顶点的平行四边形的第四个顶点D的坐标为　　．

查看试题解析
21. 学校准备用1000元购买名著和辞典作为文艺节奖品，其中名著每套60元，辞典每本40元．现已购买名著11套，最多还能买多少本辞典？

查看试题解析
22. 如图，在▱ABCD中，对角线BD的垂直平分线分别与AD，BC，BD相交于点E，F，O．

(1)、求证：四边形BEDF是菱形；

(2)、在▱ABCD中，若AB＝2.5，AD＝4，有两动点P，Q分别从B，D两点同时出发，沿△BAE和△DFC各边运动一周，即点P自B→A→E→B停止，点Q自D→F→C→D停止，点P运动的路程是x，点Q运动的路程是y，当四边形BPDQ是平行四边形时，则请直接写出x+y的值为．

查看试题解析
23. 某电商在线销售甲、乙、丙三种水果，已知每千克乙水果的售价比每千克甲水果的售价多3元，每千克丙水果的售价是每千克甲水果售价的2倍，用200元购买丙水果的数量是用80元购买乙水果数量的2倍．

(1)、求丙水果每千克的售价是多少元？

(2)、电商推出如下销售方案：甲、乙、丙三种水果搭配销售共7千克，其中乙水果的数量是丙水果数量的2倍，且甲、乙两种水果数量之和不超过丙水果数量的6倍．请直接写出按此方案购买7千克水果最少要花费元．

查看试题解析
24. 已知正方形ABCD，点E是AC上一点，延长DE交射线CB于点F，交射线AB于点G，连接BE，过点B作BH⊥BE交射线DE于点H．

(1)、如图当点G在边AB上时，
①证明：△ABE≌△ADE；
②证明：△BGH是等腰三角形；

(2)、取AG中点P，连接HP，若HP＝ $\sqrt{10}$ ，正方形周长为24，请直接写出CF的长为

查看试题解析
25. 如图，在平面直角坐标系中，两个全等的Rt△ABC和Rt△OBC的直角顶点B及一条直角边BC重合，点A，点B在x轴的负半轴上，点C在第三象限内，∠OCB＝30°，OC＝8．将△ABC绕点B按逆时针方向旋转得到△A₁BC₁（点A对应点为A₁ ，点C对应点为C₁），直线BC₁交直线OC于点D．

(1)、求点C的坐标；

(2)、当△ABC绕点B按逆时针方向旋转30°时，求直线BD的函数表达式；

(3)、当△BOD的面积为4 $\sqrt{3}$ 时，
①点E为x轴负半轴上的点，若△BDE为等腰三角形，请直接写出点E的横坐标为；

②点F为y轴正半轴上的点，若△BDF为以BD为直角边的直角三角形，请直接写出点F的坐标为

查看试题解析