辽宁省沈阳市法库县2020-2021学年八年级下学期期末数学试题

试卷更新日期：2022-04-18 类型：期末考试

进入出卷网下载

一、单选题

1. 下列四个图形中，可以由图 $1$ 通过平移得到的是（）

A、 B、 C、 D、

查看试题解析
2. 下列所给的汽车标志图案中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 多项式 $8 a^{3} b^{2} + 12 a^{3} b c - 4 a^{2} b$ 中，各项的公因式是（）

A、 $a^{2} b$ B、 $- 4 a^{2} b^{2}$ C、 $4 a^{2} b$ D、 $- a^{2} b$

查看试题解析
4. 下列各组数据中的三个数作为三角形的边长，其中能构成直角三角形的是（　　）

A、 $\sqrt{3}$ ， $\sqrt{4}$ ， $\sqrt{5}$ B、1， $\sqrt{2}$ ， $\sqrt{3}$ C、6，7，8 D、2，3，4

查看试题解析
5. 已知点A（ $a$ ，1）与点A′（5， $b$ ）关于坐标原点对称，则实数 $a$ 、 $b$ 的值是（）

A、 $a = 5, b = 1$ B、 $a = - 5, b = 1$ C、 $a = 5, b = - 1$ D、 $a = - 5, b = - 1$

查看试题解析
6. 如果m＞n，那么下列结论不正确的是（）

A、m＋2＞n＋2 B、﹣2m＞﹣2n C、2m＞2n D、m﹣2＞n﹣2

查看试题解析
7. 已知不等式组 ${\begin{array}{l} x - 2 ＜ 0 \\ x + 1 \geq 0 \end{array}$ ，其解集在数轴上表示正确的是（　　）

A、 B、 C、 D、

查看试题解析
8. 如图所示，将一个含30°角的直角三角板ABC绕点A旋转，使得点B，A，C′在同一直线上，则三角板ABC旋转的度数是（）

A、60° B、90° C、120° D、150°

查看试题解析
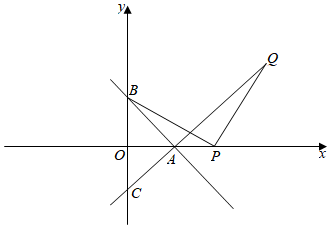
9. 如图，若一次函数y＝﹣2x+b的图象与两坐标轴分别交于A，B两点，点A的坐标为（0，3），则不等式﹣2x+b＞0的解集为（）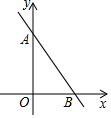

A、x＞ $\frac{3}{2}$ B、x＜ $\frac{3}{2}$ C、x＞3 D、x＜3

查看试题解析
10. 如图，在 $▱ A B C D$ 中，将 $Δ A D C$ 沿AC折叠后，点D恰好落在DC的延长线上的点E处.若 $∠ B = 60^{°}$ ， $A B =3$ ，则 $Δ A D E$ 的周长为（）

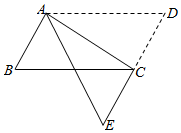A、12 B、15 C、18 D、21

查看试题解析

二、填空题

11. 分解因式： $3 x^{3} - 3 x =$ ．

查看试题解析
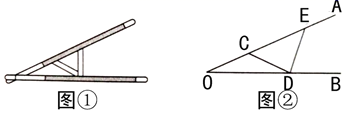
12. 若分式 $\frac{x^{2} - 1}{x - 1}$ 的值为0，则x的值为.

查看试题解析
13. 如果等腰三角形的有一个角是80°，那么顶角是度.

查看试题解析
14. “三等分角”大约是在公元前五世纪由古希腊人提出来的，借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA，OB组成，两根棒在O点相连并可绕O转动，C点固定，OC=CD=DE，点D、E可在槽中滑动．若∠BDE=75°，则∠CDE的度数是

查看试题解析
15. 如图，小明从A点出发，沿直线前进10米后向左转36°，再沿直线前进10米，再向左转36°……照这样走下去，他第一次回到出发点A点时，一共走的路程是米.

查看试题解析
16. 如图，四边形ABCD中，∠A＝90°，AB＝8，AD＝6，点M，N分别为线段BC，AB上的动点（含端点，但点M不与点B重合），点E，F分别为DM，MN的中点，则EF长度的最大值为．

查看试题解析

三、解答题

17. 解分式方程： $\frac{x}{x - 2} - 1 = \frac{4}{x^{2} - 4 x + 4}$ ．

查看试题解析
18. 先化简： $(1 - \frac{1}{x - 1}) \div \frac{x^{2} - 4 x + 4}{x^{2} - 1}$ ，再从 $- 1 \leq x \leq 2$ 的范围内选取一个合适的整数作为 $x$ 的值代入求值.

查看试题解析
19. 解不等式组： ${\begin{array}{l} 3 (x + 1) > x - 1 \\ \frac{x + 9}{2} > 2 x \end{array}$ ，并写出它的所有非负整数解．

查看试题解析
20. 如图，方格纸中每个小正方形的边长都是1个单位长度，Rt△ABC的三个顶点A(-2，2)，B(0，5)，C(0，2) ．
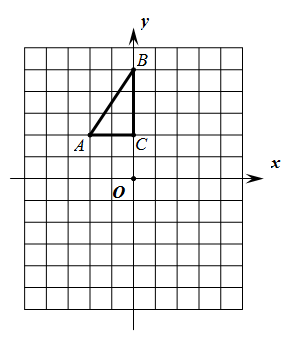
( 1 )将△ABC以点C为旋转中心旋转180°，得到△A₁B₁C，请画出△A₁B₁C的图形．
( 2 )平移△ABC，使点A的对应点A2坐标为(-2，-6)，请画出平移后对应的△A₂B₂C₂的图形．
( 3 )若将△A₁B₁C绕某一点旋转可得到△A₂B₂C₂ ，请直接写出旋转中心的坐标．

查看试题解析
21. 如图：已知AD是△ABC中BC边上的高，E是AD上一点，EB=EC，∠ABE=∠ACE．求证：∠BAE=∠CAE．
证明：在△ABC和△AEC中， ${\begin{array}{l} E B = E C \\ ∠ A B E = ∠ A C E \\ A E = A E \end{array}$
∴△ABC≌△AEC（第一步），
∴∠BAE=∠CAE（第二步）
阅读了此题及证明，上面的过程是否符合题意？若符合题意，请写出第一步的推理依据；若不符合题意，请指出错在哪一步，并写出正确的证明过程．

查看试题解析
22. 如图，等边△ABC的边长是2，D、E分别为AB、AC的中点，延长BC至点F，使CF= $\frac{1}{2}$ BC，连接CD和EF．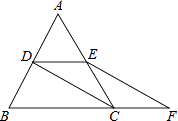

(1)、求证：DE=CF；

(2)、求EF的长．

查看试题解析
23. 为落实“美丽法库”的工作部署，县政府计划对城区道路进行了改造，现安排甲、乙两个工程队完成．已知甲队的工作效率是乙队工作效率的 $\frac{3}{2}$ 倍，甲队改造480米的道路比乙队改造同样长的道路少用4天．

(1)、求甲、乙两工程队每天能改造道路的长度分别是多少米？

(2)、若甲队工作一天需付费用7万元，乙队工作一天需付费用5万元，如需改造的道路全长1200米，改造总费用不超过145万元，至少安排甲队工作多少天？

查看试题解析
24. 如图，平行四边形ABCD中，CG⊥AB于点G，∠ABF＝45°，点F在CD上，BF交CG于点E，连接AE，AE⊥AD．

(1)、若BG＝1，BC＝ $\sqrt{5}$ ，求EF的长度；

(2)、求证：△BCG≌△EAG；

(3)、直接写出三条线段CD，CE，BE之间的数量关系．

查看试题解析
25. 如图，直线y＝﹣x＋4，与x轴、y轴分别交于A，B两点，点C与点B关于原点对称．

(1)、直接写出点A，B，C的坐标；

(2)、在线段OA的延长线上任取一点P，作PQ⊥BP，交直线AC于Q．求证：PQ＝PB；

(3)、在（2）的条件下，过点P作PM⊥AC于点M，直接写出 $\frac{M Q - A B}{P M}$ 的值．

查看试题解析