辽宁省葫芦岛市建昌县2020-2021学年八年级下学期期末数学试题
试卷更新日期:2022-04-18 类型:期末考试
一、单选题
-
1. 的绝对值是( )A、 B、 C、 D、2. 已知一组数据为1,5,3,3,7,11.则这组数据的众数和中位数分别是( )A、3,3 B、5,3 C、3,4 D、3,53. 下列各图象中,不表示 是 的函数的是( )A、
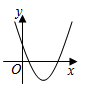 B、
B、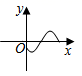 C、
C、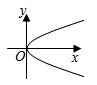 D、
D、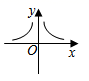 4. 下列计算中,正确的是( )A、 B、 C、÷ D、5. 如果样本方差 , 那么这个样本的平均数和样本容量分别是( )A、20,20 B、20,18 C、18,18 D、18,206. 的三边长分别为 ,下列条件:① ;② ;③ ;④ .其中能判断 是直角三角形的个数有( )A、1个 B、2个 C、3个 D、4个7. 如图,在矩形中,对角线 , 相交于点O,点E,F分别是 , 的中点,连接 , 若AB=6cm,BC=8cm.则的长是( )
4. 下列计算中,正确的是( )A、 B、 C、÷ D、5. 如果样本方差 , 那么这个样本的平均数和样本容量分别是( )A、20,20 B、20,18 C、18,18 D、18,206. 的三边长分别为 ,下列条件:① ;② ;③ ;④ .其中能判断 是直角三角形的个数有( )A、1个 B、2个 C、3个 D、4个7. 如图,在矩形中,对角线 , 相交于点O,点E,F分别是 , 的中点,连接 , 若AB=6cm,BC=8cm.则的长是( ) A、5cm B、3cm C、2.5cm D、4cm8. 如图,在一次测绘活动中,某同学站在点A的位置观测停放于B,C两处的小船,测得船B在点A北偏东75°方向900米处,船C在点A南偏东15°方向1200米处,则船B与船C之间的距离为( )
A、5cm B、3cm C、2.5cm D、4cm8. 如图,在一次测绘活动中,某同学站在点A的位置观测停放于B,C两处的小船,测得船B在点A北偏东75°方向900米处,船C在点A南偏东15°方向1200米处,则船B与船C之间的距离为( ) A、1500m B、1200m C、1000m D、800m9. 如图,菱形的边长为 , 对角线 , 交于点O, , 则菱形的面积为( )
A、1500m B、1200m C、1000m D、800m9. 如图,菱形的边长为 , 对角线 , 交于点O, , 则菱形的面积为( ) A、 B、 C、2 D、410. 已知等腰三角形的周长是10,底边长y是腰长x的函数,则下列图象中,能正确反映y与x之间函数关系的图象是( )A、
A、 B、 C、2 D、410. 已知等腰三角形的周长是10,底边长y是腰长x的函数,则下列图象中,能正确反映y与x之间函数关系的图象是( )A、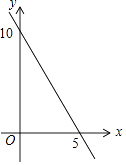 B、
B、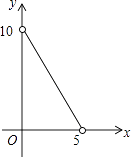 C、
C、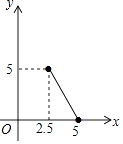 D、
D、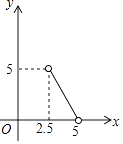
二、填空题
-
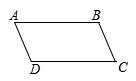
11. 化简: .12. 在实数范围内分解因式= .13. 在三次数学单元检测中,甲、乙两名同学的平均分都是92分,方差分别是 , , 则成绩较稳定的同学是 .14. 如图,▱ABCD中,∠A=∠D,则∠C= .
 15. 一次函数的图象如图所示,则一元一次不等式的解集为 .
15. 一次函数的图象如图所示,则一元一次不等式的解集为 . 16. 如图,在△ABC中,∠C=90°,∠A=30°,AB=6,以点B为圆心,BC长为半径画弧交AB于点D,再以点A为圆心,AD长为半径画弧交AC于点E,则线段CE长为 .
16. 如图,在△ABC中,∠C=90°,∠A=30°,AB=6,以点B为圆心,BC长为半径画弧交AB于点D,再以点A为圆心,AD长为半径画弧交AC于点E,则线段CE长为 . 17. 如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,几分钟后船到达点D的位置,此时绳子CD的长为10米,问船向岸边移动了米.
17. 如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,几分钟后船到达点D的位置,此时绳子CD的长为10米,问船向岸边移动了米. 18. 如图,矩形ABCD中,对角线AC与BD相交于点O,AE平分∠BAD,交BC于点E,∠CAE=15°.下列结论:①△OCD是等边三角形,②AC=2DC,③ , ④∠COE=45°.其中正确的有(填序号).
18. 如图,矩形ABCD中,对角线AC与BD相交于点O,AE平分∠BAD,交BC于点E,∠CAE=15°.下列结论:①△OCD是等边三角形,②AC=2DC,③ , ④∠COE=45°.其中正确的有(填序号).
三、解答题
-
19. 计算:
÷ .
20. 已知一次函数的图象过点(3,5)与(-4,-9).(1)、求这个一次函数的解析式.(2)、直接写出函数图象与坐标轴围成的三角形面积.21. 如图,E是▱ABCD的边AD的中点,连接CE并延长交BA的延长线于F. (1)、求证:△AEF≌△DEC.(2)、若CD=6,求BF的长.22. 甲、乙二人到某公司应聘,项目为笔试、听说、面试.若甲的这三项得分依次是92分、80分、83分,乙的这三项得分依次是90分、81分、87分.(1)、若录用这三项得分的平均分高的人,通过计算求甲、乙二人谁会被录用.(2)、若笔试、听说、面试的成绩分别按7:2:1记入总分,录用得分较高者,求甲、乙二人谁会被录用.23. 已知:在矩形ABCD中,E,F分别是AD,BC边上的点,且DE=BF.
(1)、求证:△AEF≌△DEC.(2)、若CD=6,求BF的长.22. 甲、乙二人到某公司应聘,项目为笔试、听说、面试.若甲的这三项得分依次是92分、80分、83分,乙的这三项得分依次是90分、81分、87分.(1)、若录用这三项得分的平均分高的人,通过计算求甲、乙二人谁会被录用.(2)、若笔试、听说、面试的成绩分别按7:2:1记入总分,录用得分较高者,求甲、乙二人谁会被录用.23. 已知:在矩形ABCD中,E,F分别是AD,BC边上的点,且DE=BF. (1)、求证:四边形AFCE是平行四边形.(2)、若AD=6,AB=4,EF⊥AC,求BF的长.24. 某校为了了解七年级共480名同学对防疫知识的掌握情况,对他们进行了防疫知识测试,现随机抽取甲、乙两班各15名同学的测试成绩进行整理分析,过程如下:
(1)、求证:四边形AFCE是平行四边形.(2)、若AD=6,AB=4,EF⊥AC,求BF的长.24. 某校为了了解七年级共480名同学对防疫知识的掌握情况,对他们进行了防疫知识测试,现随机抽取甲、乙两班各15名同学的测试成绩进行整理分析,过程如下:【收集数据】
甲班15名学生测试成绩分别为(单位:分):
78,83,89,96,100,85,100,94,87,90,93,92,98,95,100;
乙班15名学生测试成绩中90≤x<95的成绩如下:91,92,94,90,93.
【整理数据】
班级
75≤x<80
80≤x<85
85≤x<90
90≤x<95
95≤x<100
甲
1
1
3
4
6
乙
1
2
3
5
4
【分析数据】
班级
平均数
众数
中位数
方差
甲
92
a
93
47.3
乙
90
87
b
50.2
【应用数据】
(1)、根据以上信息填空:a= , b=;(2)、由表中数据,请根据所学知识判断哪个班的学生防疫测试的整体成绩较好?并从平均数、众数、中位数、方差中任选2个说明理由;(3)、若规定测试成绩90分及以上为优秀,根据(2)中判断结果,用成绩较好的班级的数据,估计参加防疫知识测试的480名学生中成绩为优秀的学生共有多少名.25. 在△ABC中,AB=AC,点D为射线BC上一动点(点D不与B,C重合)以AD为边作菱形ADEF,使∠DAF=∠BAC,连接CF. (1)、如图1,当点D在线段BC上时,直接写出线段BD与CF的数量关系;(2)、如图2,当点D在线段BC的延长线上,且∠BAC=90°时,
(1)、如图1,当点D在线段BC上时,直接写出线段BD与CF的数量关系;(2)、如图2,当点D在线段BC的延长线上,且∠BAC=90°时,①(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
②延长BA交CF于点G,若AB= , GF=1,请直接写出ED的长.
26. 甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地.如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题: (1)、直线OA的解析式为;(2)、求线段CD对应的函数关系式,并写出x的取值范围;(3)、轿车到达C点开始加速,直接写出小轿车在CD段与货车相距40千米时,x的值.
(1)、直线OA的解析式为;(2)、求线段CD对应的函数关系式,并写出x的取值范围;(3)、轿车到达C点开始加速,直接写出小轿车在CD段与货车相距40千米时,x的值.