辽宁省丹东市2020-2021学年八年级下学期期末数学试题
试卷更新日期:2022-04-18 类型:期末考试
一、单选题
-
1. 若 , 则下列不等式中不成立的是( )A、 B、 C、 D、2. 下列图形:平行四边形、等腰三角形、线段、正六边形、圆,其中既是中心对称图形又是轴对称图形的有( )A、1个 B、2个 C、3个 D、4个3. 下列各式从左到右的变形中,是因式分解的是( )A、 B、 C、 D、4. 下列各式中x、y的值均扩大为原来的2倍,则分式的值一定保持不变的是( )A、 B、 C、 D、5. 若关于x的分式方程 =1的解为x=2,则m的值为( )A、5 B、4 C、3 D、26. 如图,在中, , 交于点D, , , 则的长( )
 A、8 B、10 C、11 D、127. 如图,将绕点A按逆时针方向旋转80°,得到 , 连接 , 若 , 的度数为( )
A、8 B、10 C、11 D、127. 如图,将绕点A按逆时针方向旋转80°,得到 , 连接 , 若 , 的度数为( ) A、20° B、30° C、25° D、35°8. 如图,一次函数图象经过点 , 与正比例函数的图象交于点B,则不等式的解集为( )
A、20° B、30° C、25° D、35°8. 如图,一次函数图象经过点 , 与正比例函数的图象交于点B,则不等式的解集为( )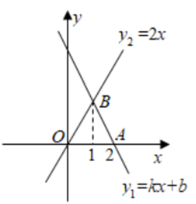 A、 B、 C、 D、9. 如图,在中, , , 的平分线与的垂直平分线交于点O,点E在上,点F在上,连接 , 将沿折叠,点C与点恰好重合时,则的度数( )
A、 B、 C、 D、9. 如图,在中, , , 的平分线与的垂直平分线交于点O,点E在上,点F在上,连接 , 将沿折叠,点C与点恰好重合时,则的度数( ) A、90° B、92° C、95° D、98°
A、90° B、92° C、95° D、98°二、填空题
-
10. 如果分式 有意义,那么 的取值范围是.11. 已知一个正多边形的一个内角是120º,则这个多边形的边数是 .12. 若 , 则的值为 .13. 如图:在 中, , 平分 交 于点D,且 , ,则点D到 的距离为.
 14. 不等式的正整数解为 .15. 如图, , D、E分别是、的中点,平分 , 交于点F,若 , , 则的长是 .
14. 不等式的正整数解为 .15. 如图, , D、E分别是、的中点,平分 , 交于点F,若 , , 则的长是 . 16. 关于x的分式方程的解为非负数,则实数m的取值范围 .17. 如图,四边形中, , cm,cm,点P以1cm/s的速度由A点向B点运动,同时点Q以2cm/s的速度由C点向D点运动,其中一点到达终点时,另一点也停止运动,当线段将四边形截出一个平行四边形时,此时的运动时间为s.
16. 关于x的分式方程的解为非负数,则实数m的取值范围 .17. 如图,四边形中, , cm,cm,点P以1cm/s的速度由A点向B点运动,同时点Q以2cm/s的速度由C点向D点运动,其中一点到达终点时,另一点也停止运动,当线段将四边形截出一个平行四边形时,此时的运动时间为s. 18. 如图,是的内角平分线,是的外角平分线,过A分别作、 , 垂足分别为F、G,连接 , 若 , , , 则的长度为 .
18. 如图,是的内角平分线,是的外角平分线,过A分别作、 , 垂足分别为F、G,连接 , 若 , , , 则的长度为 .
三、解答题
-
19.(1)、因式分解:(2)、解不等式组: , 并把解集表示在数轴上.20.(1)、先化简,再求值: , 其中 .(2)、解方程:21. 如图,在平面直角坐标系中,网格的每个小方格都是边长为1个单位长度的正方形,的顶点均落在格点上.

( 1 )将先向右平移6个单位长度再向下平移1个单位长度,得到 , 在网格中画出;
( 2 )作关于x轴的轴对称图形,得到 , 在网格中画出 .
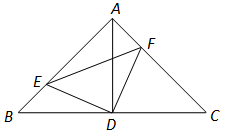
22. 如图,在中, , , 点D为的中点,E、F分别是 , 上的点,且 , 连接、、、 .求证:①≌ ②
 23. 某服装厂准备加工260套运动服,在加工了60套后,采用新技术,使每天的工作效率是原来的2倍,结果共用了8天完成,求该厂原来每天加工多少套运动服.24. 如图,在 中,过点B作 ,交 于点E,交 于点M,过点D作 ,交 于点 ,交 于点N.
23. 某服装厂准备加工260套运动服,在加工了60套后,采用新技术,使每天的工作效率是原来的2倍,结果共用了8天完成,求该厂原来每天加工多少套运动服.24. 如图,在 中,过点B作 ,交 于点E,交 于点M,过点D作 ,交 于点 ,交 于点N. (1)、求证:四边形 是平行四边形;(2)、已知 ,求 的长.25. 甲、乙两家商场以相同的价格出售同样的商品,为了吸引顾客各自推出不同的优惠方案:在甲商场购买商品超过300元之后,超过部分按8折优惠;在乙商场购买商品超过200元之后,超过部分按8.5折优惠,设甲商场实际付费为元,乙商场实际付费为元,顾客购买商品金额为x元 .(1)、分别求出 , 与x的函数关系式;(2)、比较顾客到哪个商场更优惠,并说明理由.26. 在中, , , 将沿方向平移得到 , A,C的对应点分别是D、E,连接交于点O.
(1)、求证:四边形 是平行四边形;(2)、已知 ,求 的长.25. 甲、乙两家商场以相同的价格出售同样的商品,为了吸引顾客各自推出不同的优惠方案:在甲商场购买商品超过300元之后,超过部分按8折优惠;在乙商场购买商品超过200元之后,超过部分按8.5折优惠,设甲商场实际付费为元,乙商场实际付费为元,顾客购买商品金额为x元 .(1)、分别求出 , 与x的函数关系式;(2)、比较顾客到哪个商场更优惠,并说明理由.26. 在中, , , 将沿方向平移得到 , A,C的对应点分别是D、E,连接交于点O.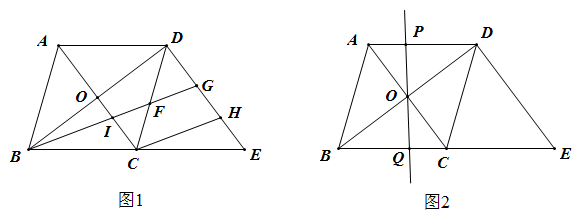 (1)、如图1,将直线绕点B顺时针旋转,与、、分别相交于点I、F、G,过点C作交于点H.
(1)、如图1,将直线绕点B顺时针旋转,与、、分别相交于点I、F、G,过点C作交于点H.①求证:≌
②若 , 求的长;
(2)、如图2,将直线绕点O逆时针旋转 , 与线段、分别交于点P、Q,在旋转过程中,四边形的面积是否发生变化?若不变,求出四边形的面积,若变化,请说明理由;(3)、在(2)的旋转过程中,能否为等腰三角形,若能,请直接写出的长,若不能,请说明理由.