辽宁省大连市高新区2020-2021学年八年级下学期期末数学试题

试卷更新日期：2022-04-18 类型：期末考试

进入出卷网下载

一、单选题

1. 使代数式 $\sqrt{x - 1}$ 有意义的x的取值范围是（）

A、 $x ⩾ - 1$ B、 $x > - 1$ C、 $x ⩾ 1$ D、 $x > 1$

查看试题解析
2. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{3}$ B、 $\sqrt{0.5}$ C、 $\sqrt{8}$ D、 $\sqrt{\frac{1}{3}}$

查看试题解析
3. 下列四组线段中，能组成直角三角形的是（　　）.

A、a=1，b=2，c=3 B、a=2，b=3，c=4 C、a=2，b=4，c=5 D、a=3，b=4，c=5

查看试题解析
4. 下列运算正确的是（　　）

A、 $\sqrt{5} + \sqrt{3} = \sqrt{8}$ B、 $\sqrt{12} - \sqrt{3} = 2 \sqrt{3}$ C、 $\sqrt{3} \times \sqrt{2}$ ＝6 D、 $\sqrt{3}$ ÷ $\sqrt{\frac{1}{3}}$ ＝3

查看试题解析
5. 已知正比例函数 $y = k x (k \neq 0)$ 的图象经过点 $(2 ， - 3) ，$ 则k的值为（）

A、 $\frac{3}{2}$ B、 $- \frac{2}{3}$ C、 $- \frac{3}{2}$ D、 $\frac{2}{3}$

查看试题解析
6. 四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（）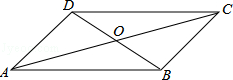

A、AB//DC，AD//BC B、AB=DC，AD=BC C、AO=CO，BO=DO D、AB//DC，AD=BC

查看试题解析

7. 某校为了解学生的课外阅读情况，随机抽取了一个班的学生，对他们一周的课外阅读时间进行了统计，统计数据如下表，则该班学生一周课外阅读时间的中位数和众数分别是（）

读书时间	6 小时及以下	7 小时	8 小时	9 小时	10 小时及以上
学生人数	6	11	8	8	7

A、8，7 B、8，8 C、8.5，8 D、8.5，7

查看试题解析

8. 如图，在菱形 $A B C D$ 中， $A C$ 与 $B D$ 交于点O，点E为 $B C$ 中点，连接 $O E$ ，若菱形 $A B C D$ 的周长为16，则线段 $O E$ 的长为（）

A、3 B、2.5 C、2 D、1.5

查看试题解析
9. 某商场为了增加销售额，推出“元旦销售大酬宾”活动，其活动内容为：“凡一月份在该商场一次性购物超过100元以上者，超过100元的部分按9折优惠．”在大酬宾活动中，小王到该商场为单位购买单价为60元的办公用品x件（x＞2），则应付货款y（元）与商品件数x的函数关系式（）

A、y＝54x（x＞2） B、y＝54x＋10（x＞2） C、y＝54x－90（x＞2） D、y＝54x＋100（x＞2）

查看试题解析
10. 关于一次函数 $y = (k - 1) x + 1 - k$ ，下列说法：
①当 $k > 1$ 时，图象从左向右上升，y随x的增大而增大；
②当 $k < 1$ 时，图象经过第二、三、四象限；
③函数图象一定过点 $(1 ， 0)$ ．
其中正确的是（）

A、①② B、①③ C、②③ D、①②③

查看试题解析

二、填空题

11. 在平行四边形 $A B C D$ 中， $∠ B A D = 50 °$ ，则 $∠ A B C =$ °．

查看试题解析
12. 要从甲，乙两名运动员中选出一名参加市运会射击项目比赛，对这两名运动员进行了10次射击测试，经过数据分析，甲，乙两名运动员的平均成绩均为8（环），甲的方差为1.2（环²），乙的方差为1（环²），则这10次测试成绩比较稳定的运动员是（填“甲”、“乙”）.

查看试题解析
13. 一次函数 $y = k x + b$ （ $k \neq 0$ ，且k，b为常数）的图象如图所示，则关于x的不等式 $k x + b < 0$ 的解集是．

查看试题解析
14. 我国古代数学著作《九章算术》记载了一道有趣的问题．原文是：今有池方一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐．问水深、葭长各几何．译为：有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根芦苇，它高出水面1尺，如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面，水的深度与这根芦苇的长度分别是多少？设芦苇的长度是x尺．根据题意，可列方程为．

查看试题解析
15. 如图，在平面直角坐标系中，直线 $y = \frac{3}{4} x + 3$ 交x轴于点A，交y轴于点B，点C在x轴正半轴上， $A B = A C$ ，则 $△ A B C$ 的面积为．

查看试题解析
16. 如图，矩形 $A B C D$ 中， $A D = 2 A B$ ，将矩形 $A B C D$ 沿直线 $E F$ 折叠，使点C与点A重合，折痕交 $B C$ 于点E，交 $A D$ 于点F，设 $A B = x$ ， $A F = y$ ，则y关于x的函数关系式为．

查看试题解析

三、解答题

17. 计算 $(2 \sqrt{2} - 1)^{2} - \sqrt{(- 7)^{2}} - \sqrt{\frac{1}{2}}$ ．

查看试题解析
18. 某学校抽查了某班级某月8天的用电量，数据如下表：
用电量（度）
8
9
10
13
15
天数
1
1
3
2
1

(1)、求这个班级平均每天的用电量；

(2)、已知该校共有15个班级，该月共有20天上学需要用电，估计该校该月总的用电量．

查看试题解析
19. 如图，在平行四边形ABCD中，E是BC上一点，点F在线段DE上，DE=AD，且∠AFE=∠ADC，求证：DF=EC．

查看试题解析
20. 小明爸爸为了让小明上学更近，决定在学校附近租套房子居住．现有甲、乙两家出租房屋，甲家已经装修好，每月租金为2500元；乙家未装修，每月租金为1800元，但需要支付装修费14000元．设租用时间为x个月，所需租金为y元．

(1)、请分别写出租用甲、乙两家房屋的租金 $x_{甲}$ 、 $x_{乙}$ 与租用时间x之间的函数关系；

(2)、试判断租用哪家房屋更合算，并说明理由．

查看试题解析
21. 某小区有一块如图所示的四边形空地 $A B C D$ ，为了庆祝建党百年，小区物业决定在这块空地上种植花草，测得 $A B = A D = 10 m$ ， $C D = 26 m$ ， $B C = 24 m$ ， $∠ A = 60 °$ ．种植花草的费用为80元/ $m^{2}$ ，则该空地种植花草共需多少元？（参考数据： $\sqrt{3} \approx 1.732$ ）

查看试题解析
22. 如图，在菱形ABCD中，对角线AC，BD交于点O，过点A作AE⊥BC于点E，延长BC到点F，使CF=BE，连接DF．

(1)、求证：四边形AEFD是矩形；

(2)、连接OE，若AD=5，EC=2，求OE的长度．

查看试题解析
23. 甲、乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发向乙地，轿车必货车晚出发1.5小时，如图，线段OA表示货车离甲地的距离y（千米）与时间x（小时）之间的函数关系．请根据图象解答下列问题：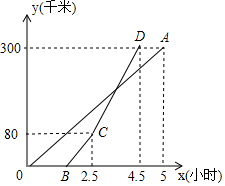

(1)、轿车到乙地时，求货车与甲地的距离；

(2)、求线段CD对应的函数表达式；

(3)、在轿车行进过程，轿车行驶多少时间，两车相距15千米．

查看试题解析
24. 在平面直角坐标系中，直线 $y = - 2 x - 4$ 与x轴，y轴分别交于点A、B，与直线 $y = 3$ 交于点C，点D为直线 $y = 3$ 上点C右侧的一点．

(1)、如图1，若 $△ A C D$ 的面积为6，则点D的坐标为；

(2)、如图2，当 $∠ C A D = 45 °$ 时，求直线 $A D$ 的解析式；

(3)、在（2）的条件下，点E为直线 $A D$ 上一点，设点E的横坐标为m， $△ A C E$ 的面积为S，求S关于m的函数关系式，并直接写出自变量m的取值范围．

查看试题解析
25. 如图．在正方形 $A B C D$ 中，点E在 $B C$ 边上，点F在 $C D$ 延长线上， $B E = D F$ ，连接 $E F$ 交 $B D$ 于点H，连接 $A H$ ．

(1)、求证 $H E = H F$ ；

(2)、求 $\frac{A H}{E F}$ 的值；

(3)、探究 $A B$ 、 $B E$ 、 $B H$ 三条线段之间的数量关系，并证明．

查看试题解析
26. 已知函数 $y = {\begin{array}{l} x + 3 m ， x ⩾ m ， \\ - x + 5 m ， x < m . \end{array}$ 其中m为常数，该函数图象记为G．

(1)、当 $m = 1$ 时，
①若点A（a，6）在图象G上，求a的值；
②当 $- 1 ⩽ x ⩽ 2$ 时，求函数值y的取值范围．

(2)、点B在图象G上，点B的横坐标为2m，直线 $y = 6 m$ 与图象G交于点C、D，当 $△ B C D$ 的面积为4时，求m的值；

(3)、直线 $x = 4 m$ 与图象G交于点M，与直线 $y = 2 x - 1$ 交于点N，当 $\frac{3}{5} ⩽ M N ⩽ \frac{3}{4}$ 时，直接写出m的取值范围．

查看试题解析

用电量（度）	8	9	10	13	15
天数	1	1	3	2	1