辽宁省朝阳市凌源市2020-2021学年八年级下学期期末数学试题

试卷更新日期：2022-04-18 类型：期末考试

进入出卷网下载

一、单选题

1. 下列数组中，能构成直角三角形的是（）

A、1，1， $\sqrt{3}$ B、 $\sqrt{2}$ ， $\sqrt{3}$ ， $\sqrt{5}$ C、0.2，0.3，0.5 D、 $\frac{1}{3}$ ， $\frac{1}{4}$ ， $\frac{1}{5}$

查看试题解析
2. 下列是最简二次根式的为（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{0.8}$ C、 $\sqrt{81}$ D、 $\sqrt{34}$

查看试题解析
3. 下列命题不正确的是（）

A、平行四边形的对角相等 B、对角线互相垂直的四边形是菱形 C、两条对角线相等的平行四边形是矩形 D、正方形的对角线相等且互相垂直

查看试题解析
4. 已知点(﹣3，y₁)，(-5，y₂)都在直线y=kx+2（k＞0）上，则y₁ ， y₂大小关系是（）

A、y₁＞y₂ B、y₁=y₂ C、y₁＜y₂ D、不能比较

查看试题解析
5. 期末考试后，办公室里有两位数学老师正在讨论他们班的数学考试成绩，林老师：“我班的学生考得还不错，有一半的学生考79分以上，一半的学生考不到79分．”王老师：“我班大部分的学生都考在80分到85分之间喔．”依照上面两位老师所叙述的话你认为林、王老师所说的话分别针对（　　）

A、平均数、众数 B、平均数、极差 C、中位数、方差 D、中位数、众数

查看试题解析
6. 函数 $y = \sqrt{x - 2}$ 中自变量x的取值范围是（）

A、 $x \geq 2$ B、 $x > 2$ C、 $x \leq 2$ D、 $x < 2$

查看试题解析
7. 如图所示，某产品的生产流水线每小时可生产100件产品，生产前没有产品积压，生产3h后安排工人装箱，若每小时装产品150件，未装箱的产品数量（y）是时间（x）的函数，那么这个函数的大致图像只能是（　）

A、 B、 C、 D、

查看试题解析
8. 如图，在Rt $△$ ABC中，∠B＝90°，AB＝3，BC＝4，将 $△$ ABC折叠，使点B恰好落在边AC上，与点 $B^{'}$ 重合，AE为折痕，则E $B^{'}$ 长为（）

A、3cm B、2.5cm C、1.5cm D、1cm

查看试题解析
9. 直线y= ax +2与直线y= bx + 3相交于x轴上一点，则a：b =（）

A、2：3 B、3：2 C、-2：3 D、-3：2

查看试题解析
10. 如图，在菱形 $A B C D$ 中，P是对角线 $A C$ 上一动点，过点P作 $P E ⊥ B C$ 于点E. $P F ⊥ A B$ 于点F.若菱形 $A B C D$ 的周长为20，面积为24，则 $P E + P F$ 的值为（）

A、4 B、 $\frac{24}{5}$ C、6 D、 $\frac{48}{5}$

查看试题解析

二、填空题

11. 甲、乙两人在相同条件下进行射击练习，每人10次射击成绩的平均值都是7环，方差分别为 $S_{甲}^{2} = 2.9 ， S_{乙}^{2} = 1.2$ ，则两人成绩比较稳定的是.(填“甲”或“乙”)

查看试题解析
12. 比较大小：-3 $\sqrt{2}$ -2 $\sqrt{3}$

查看试题解析
13. 在▱ABCD中，∠A的平分线分BC成4cm和3cm的两条线段，则▱ABCD的周长为

查看试题解析
14. 顺次连接对角线互相垂直的四边形各边中点所得的四边形一定是．

查看试题解析
15. 一次函数y＝3x + m的图象与两坐标轴所围成的三角形面积为54，则m = ．

查看试题解析
16. 由四个全等的直角三角形组成如图所示的“赵爽弦图”，若直角三角形两直角边边长的和为3，面积为1，则图中阴影部分的面积为．

查看试题解析
17. 两组数据m，6，n与1，m，2n，7的平均数都是6，若将这两组数据合并成一组数据，则这组新数据的中位数为．

查看试题解析
18. 在矩形ABCD中，AB=6，BC=9，E是CD边的中点，过点E作直线EM垂直直线AE交BC边于点M，连接AM．则AM的长为．

查看试题解析

三、解答题

19. 计算

(1)、 $\sqrt{8} - 6 \sqrt{\frac{1}{3}} - \sqrt{2} + 2 \sqrt{12}$

(2)、 $\sqrt{24} \div \sqrt{3} - \sqrt{\frac{1}{2}} \times \sqrt{6} + \sqrt{12}$

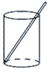
查看试题解析
20. 一种盛饮料的圆柱形杯，测得内部底面半径为2.5㎝，高为12㎝，吸管放进杯里，杯口外面至少要露出4.6㎝，问吸管要做多长？

查看试题解析
21. 如图，已知∠AOB，OA＝OB，点E在边OB上，四边形AEBF是平行四边形．

(1)、请你只用无刻度的直尺在图中画出∠AOB的平分线．（保留作图痕迹，不写作法）

(2)、请说明你的画法的符合题意性．

查看试题解析
22. 某公司销售部有营销人员15人，销售部为了制定某种商品的月销售定额，统计了这15人某月的销售量如下：
每人销售件数
1800
510
250
210
150
120
人数
1
1
3
5
3
2

(1)、求这15位营销人员该月销售量的平均数、中位数和众数；

(2)、假设销售负责人把每位营销员的月销售额定为320件，你认为是否合理，为什么？如不合理，请你制定一个较合理的销售定额，并说明理由．

查看试题解析
23.

(1)、已知： $x = \sqrt{2} - 1$ ，求 $x^{2} + 2 x - 3$ 的值．

(2)、已知 $a = \sqrt{5} + 2$ ， $b = \sqrt{5} - 2$ ，求 $\sqrt{\frac{a}{b} + \frac{b}{a} + 7}$ 的值．

查看试题解析
24.
如图，已知四边形ABCD为平行四边形，AE⊥BD于E，CF⊥BD于F．

(1)、求证：BE＝DF；

(2)、若M、N分别为边AD、BC上的点，且DM=BN，试猜想四边形MENF的形状，并证明你的结论．

查看试题解析
25. 甲、乙两个探测气球分别从海拔 $5 m$ 和 $15 m$ 处同时出发，匀速上升 $60 min$ .下图是甲、乙两个探测气球所在位置的海拔y（单位：m）与气球上升时间x（单位： $\min$ ）的函数图象.

(1)、求这两个气球在上升过程中y关于x的函数解析式；

(2)、当这两个气球的海拔高度相差 $15 m$ 时，求上升的时间.

查看试题解析
26. 如图，已知矩形ABCD中，延长BC至E，使BE=BD，F为DE的中点，连接AF、CF．若AB=3，AD=4．

(1)、求CF的长；

(2)、求证：CF⊥AF．

(3)、若矩形ABCD的边长为任意值时，其它条件不变，CF ⊥ AF还成立吗？（只答“成立”或“不成立”，不用说明理由）

查看试题解析

每人销售件数	1800	510	250	210	150	120
人数	1	1	3	5	3	2