辽宁省朝阳市朝阳县2020-2021学年八年级下学期期末数学试题
试卷更新日期:2022-04-18 类型:期末考试
一、单选题
-
1. 计算×的结果是( )A、 B、8 C、4 D、±42. 当x=3时,函数y=-2x+1的值是( )A、3 B、-5 C、7 D、53. 若正比例函数y=kx的图象经过点(2,1),则k的值为( )A、﹣ B、 C、﹣2 D、24. 正方形的一条对角线之长为4,则此正方形的面积是( )A、16 B、4 C、8 D、85. 在中, , , , 则点C到的距离是( )A、 B、 C、 D、6. 满足下列条件的四边形,不一定是平行四边形的是( )A、两组对边分别平行 B、两组对边分别相等 C、一组对边平行且相等 D、一组对边平行,另一组对边相等7. 如图,直线:与直线:相交于点 , 则关于x的不等式的解集为( )
 A、 B、 C、 D、8. 某校有甲、乙两个合唱队,两队队员的平均身高都为 , 标准差分别是、 , 且 , 则两个队的队员的身高较整齐的是( )A、甲队 B、两队一样整齐 C、乙队 D、不能确定9. 学校离小林家距离为2千米,某天他放学后骑自行车回家,行驶了5分钟后,因故停留10分钟,然后又行驶了5分钟到家,在下列图形中能大致描述他回家过程中离家的距离s(千米)与所用时间t(分)之间的函数关系是( )A、
A、 B、 C、 D、8. 某校有甲、乙两个合唱队,两队队员的平均身高都为 , 标准差分别是、 , 且 , 则两个队的队员的身高较整齐的是( )A、甲队 B、两队一样整齐 C、乙队 D、不能确定9. 学校离小林家距离为2千米,某天他放学后骑自行车回家,行驶了5分钟后,因故停留10分钟,然后又行驶了5分钟到家,在下列图形中能大致描述他回家过程中离家的距离s(千米)与所用时间t(分)之间的函数关系是( )A、 B、
B、 C、
C、 D、
D、 10. 如图,在中, , , 点D在上, , , 则的长为( )
10. 如图,在中, , , 点D在上, , , 则的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
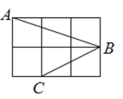
11. 函数y= –1的自变量x的取值范围是.12. 比较大小:4(填入“>”或“<”号)13. 如图,每个小正方形的边长都相等, , , 是小正方形的顶点,则的度数为 .
 14. 把直线y=x+1沿x轴向右平移2个单位,所得直线的函数解析式为 .15. 已知一组数据3,a,4,6,7,它们的平均数是5,则这组数据的方差是 .16. 如图是“赵爽弦图”,△BCG、、和是四个全等的直角三角形,四边形和都是正方形,如果 , , 那么等于 .
14. 把直线y=x+1沿x轴向右平移2个单位,所得直线的函数解析式为 .15. 已知一组数据3,a,4,6,7,它们的平均数是5,则这组数据的方差是 .16. 如图是“赵爽弦图”,△BCG、、和是四个全等的直角三角形,四边形和都是正方形,如果 , , 那么等于 . 17. 直线在直角坐标系中的图象如图所示,化简 .
17. 直线在直角坐标系中的图象如图所示,化简 . 18. 如图,为的中位线,点F在上,且为直角.若 , , 则的长为 .
18. 如图,为的中位线,点F在上,且为直角.若 , , 则的长为 . 19. 如图, , 过P作且 , 由勾股定理得;再过P作且 , 得;又过作且 , 得;…依次类推,得 .
19. 如图, , 过P作且 , 由勾股定理得;再过P作且 , 得;又过作且 , 得;…依次类推,得 . 20. 如图,把放在平面直角坐标系内,其中 , , 点A,B的坐标分别为 , , 将沿x轴向右平移,当点C落在直线上时,线段扫过的面积为 .
20. 如图,把放在平面直角坐标系内,其中 , , 点A,B的坐标分别为 , , 将沿x轴向右平移,当点C落在直线上时,线段扫过的面积为 .
三、解答题
-
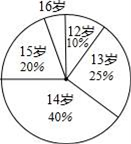
21. 计算:(1)、;(2)、 .22. 某中学抽样调查后得到n名学生年龄情况,将结果绘制成如图的扇形统计图.
 (1)、被调查学生年龄的中位数是 , 众数是;(2)、被调查的学生中12岁学生比16岁学生多30人,通过计算求14岁学生的人数;(3)、通过计算求该学校学生年龄的平均数(精确到1岁).23. 已知直线y=kx+b经过点A(5,0),B(1,4).
(1)、被调查学生年龄的中位数是 , 众数是;(2)、被调查的学生中12岁学生比16岁学生多30人,通过计算求14岁学生的人数;(3)、通过计算求该学校学生年龄的平均数(精确到1岁).23. 已知直线y=kx+b经过点A(5,0),B(1,4).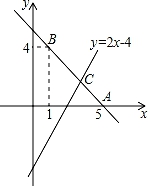 (1)、求直线AB的解析式;(2)、若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;(3)、根据图象,写出关于x的不等式2x﹣4>kx+b的解集.24. 如图,平行四边形中, , 点E,F分别在和的延长线上, , , .
(1)、求直线AB的解析式;(2)、若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;(3)、根据图象,写出关于x的不等式2x﹣4>kx+b的解集.24. 如图,平行四边形中, , 点E,F分别在和的延长线上, , , .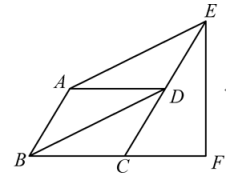 (1)、求证:四边形平行四边形;(2)、求的长.
(1)、求证:四边形平行四边形;(2)、求的长.
