云南省昭通市永善、绥江县2021-2022学年高一数学3月月考试卷
试卷更新日期:2022-04-18 类型:月考试卷
一、单选题
-
1. 设集合 , 则( )A、 B、 C、 D、2. 化简 得( )A、 B、 C、 D、3. 函数的定义域是( )A、 B、 C、 D、4. 已知弧度的圆心角所对的弦长为 , 那么这个圆心角所对的弧长是( )A、2 B、 C、 D、5. 已知 ,则 ( )A、-7 B、7 C、-1 D、16. 已知 , 则a,b,c的大小关系为( )A、 B、 C、 D、7. 若 , 则下列结论不正确的是( )A、 B、 C、 D、8. 函数 的图象大致为( )A、
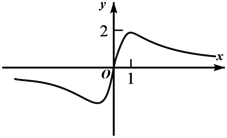 B、
B、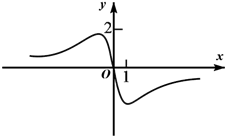 C、
C、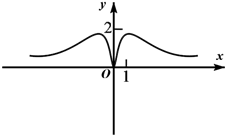 D、
D、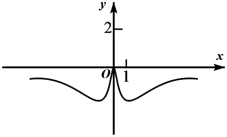
二、多选题
-
9. 下列有关向量命题,不正确的是( )A、若 ,则 B、已知 ,且 ,则 C、若 ,则 D、若 ,则 且10. 下列四个命题正确的是( )A、函数的图象过定点; B、已知函数是定义在上的奇函数,当时, , 若 , 则实数或; C、若 , 则的取值范围是; D、对于函数 , 其定义域内任意都满足 .11. 已知函数的部分图象如图所示,下列说法正确的是( )
 A、函数的图象关于点对称 B、函数的图象关于直线对称 C、函数在单调递减 D、该图象向右平移个单位可得的图象12. 已知函数 ,方程 有4个不同的实数根,则下列选项正确的为( )A、函数 的零点的个数为2 B、实数 的取值范围为 C、函数 无最值 D、函数 在 上单调递增
A、函数的图象关于点对称 B、函数的图象关于直线对称 C、函数在单调递减 D、该图象向右平移个单位可得的图象12. 已知函数 ,方程 有4个不同的实数根,则下列选项正确的为( )A、函数 的零点的个数为2 B、实数 的取值范围为 C、函数 无最值 D、函数 在 上单调递增三、填空题
-
13. 若 ,则 .14. 已知向量 的夹角为 ,且 ,则 .15. 命题“”为真,则实数a的范围是16. 已知函数 , 若 , 则实数的取值范围是.
四、解答题
-
17. 计算:(1)、(2)、18. 已知集合 , , .(1)、求;(2)、若是“”的充分不必要条件,求实数的取值范围.19. 已知函数(其中)的图象如图所示.
 (1)、求函数的解析式;(2)、若将函数的图象上的所有点的纵坐标不变,横坐标伸长到原来的3倍,得到函数的图象,求当时,函数的最大值及最小值.20. 生命在于运动,运动在于锻炼.其中,游泳就是一个非常好的锻炼方式.游泳有众多好处:强.身健体;保障生命安全;增强心肺功能;锻炼意志,培养勇敢顽强精神;休闲娱乐,促进身心健康.近几年,游泳池成了新小区建设的标配.家门口的“游泳池”,成了市民休闲娱乐的好去处.如图,某小区规划一个深度为 , 底面积为的矩形游泳池,按规划要求:在游泳池的四周安排宽的休闲区,休闲区造价为元 , 游泳池的底面与墙面铺设瓷砖,瓷砖造价为元.其他设施等支出大约为万元,设游泳池的长为.
(1)、求函数的解析式;(2)、若将函数的图象上的所有点的纵坐标不变,横坐标伸长到原来的3倍,得到函数的图象,求当时,函数的最大值及最小值.20. 生命在于运动,运动在于锻炼.其中,游泳就是一个非常好的锻炼方式.游泳有众多好处:强.身健体;保障生命安全;增强心肺功能;锻炼意志,培养勇敢顽强精神;休闲娱乐,促进身心健康.近几年,游泳池成了新小区建设的标配.家门口的“游泳池”,成了市民休闲娱乐的好去处.如图,某小区规划一个深度为 , 底面积为的矩形游泳池,按规划要求:在游泳池的四周安排宽的休闲区,休闲区造价为元 , 游泳池的底面与墙面铺设瓷砖,瓷砖造价为元.其他设施等支出大约为万元,设游泳池的长为. (1)、试将总造价(元)表示为长度的函数;(2)、当取何值时,总造价最低,并求出最低总造价.
(1)、试将总造价(元)表示为长度的函数;(2)、当取何值时,总造价最低,并求出最低总造价.