2022年中考数学二轮专题复习-规律探索
试卷更新日期:2022-04-17 类型:二轮复习
一、单选题
-
1. 一列数1,3,7,13,…,按此规律排列,第6个数是( )A、21 B、31 C、43 D、572. 正方形ABCD在数轴上的位置如图所示,点D,A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2019次后,数轴上数2019所对应的点是( )
 A、点C B、点D C、点A D、点B3. 某人的身份证号码是320922199904010012,此人的生日是( )A、9月4日 B、10月1日 C、4月1日 D、9月22日4. 观察下列图形,图(1)中有3个三角形,图(2)中有5个三角形,图(3)中有7个三角形,…若依此规律下去,则第5个图形中三角形的个数是( )
A、点C B、点D C、点A D、点B3. 某人的身份证号码是320922199904010012,此人的生日是( )A、9月4日 B、10月1日 C、4月1日 D、9月22日4. 观察下列图形,图(1)中有3个三角形,图(2)中有5个三角形,图(3)中有7个三角形,…若依此规律下去,则第5个图形中三角形的个数是( ) A、9个 B、11个 C、13个 D、15个5. 我国是最早认识负数,并进行相关运算的国家在古代数学名著《九章算术》里,就记载了利用算筹实施“正负术”的方法,图1表示的是计算 的过程按照这种方法,图2表示的过程应是在计算( )
A、9个 B、11个 C、13个 D、15个5. 我国是最早认识负数,并进行相关运算的国家在古代数学名著《九章算术》里,就记载了利用算筹实施“正负术”的方法,图1表示的是计算 的过程按照这种方法,图2表示的过程应是在计算( )
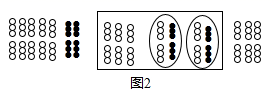 A、 B、 C、5+2 D、6. 如图,小明用棋子摆了几个“开”字,其中第①个“开”字用了14个棋子,第②个“开”字用了20个棋子,第③个“开”字用了26个棋子…,照此规律继续摆下去,第7个图需用到的棋子数为( )
A、 B、 C、5+2 D、6. 如图,小明用棋子摆了几个“开”字,其中第①个“开”字用了14个棋子,第②个“开”字用了20个棋子,第③个“开”字用了26个棋子…,照此规律继续摆下去,第7个图需用到的棋子数为( )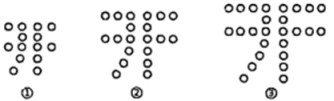 A、38 B、44 C、50 D、567. 如图,直线 与 轴、 轴分别相交于点A、B,过点B作 ,使 .将 绕点 顺时针旋转,每次旋转 .则第2022次旋转结束时,点 的对应点 落在反比例函数 的图象上,则 的值为
A、38 B、44 C、50 D、567. 如图,直线 与 轴、 轴分别相交于点A、B,过点B作 ,使 .将 绕点 顺时针旋转,每次旋转 .则第2022次旋转结束时,点 的对应点 落在反比例函数 的图象上,则 的值为 A、-4 B、4 C、-6 D、68. 如图,宽为30 cm的长方形图案由10个相同的小长方形拼成,其中一个小长方形的长为( )
A、-4 B、4 C、-6 D、68. 如图,宽为30 cm的长方形图案由10个相同的小长方形拼成,其中一个小长方形的长为( ) A、10 cm B、18 cm C、20 cm D、24 cm9. 如图是用灰白两种颜色的纸片按一定的规律摆成的图案,依此规律继续摆下去,若第n个图案中白色纸片的个数是1564,则n的值为( )
A、10 cm B、18 cm C、20 cm D、24 cm9. 如图是用灰白两种颜色的纸片按一定的规律摆成的图案,依此规律继续摆下去,若第n个图案中白色纸片的个数是1564,则n的值为( ) A、520 B、521 C、523 D、52410. 现有一列式子:① ;② ;③ ,则第⑧个式子的计算结果用科学记数法可表示为( )A、 B、 C、 D、11. 如图,在平面直角坐标系中,将等边 绕点A旋转180°,得到 ,再将 绕点 旋转180°,得到 ,再将 绕点 旋转180°,得到 ,…,按此规律进行下去,若点 ,则点 的坐标为( )
A、520 B、521 C、523 D、52410. 现有一列式子:① ;② ;③ ,则第⑧个式子的计算结果用科学记数法可表示为( )A、 B、 C、 D、11. 如图,在平面直角坐标系中,将等边 绕点A旋转180°,得到 ,再将 绕点 旋转180°,得到 ,再将 绕点 旋转180°,得到 ,…,按此规律进行下去,若点 ,则点 的坐标为( ) A、 B、 C、 D、12. 将数按以下规律排列:1,2,3,2,5,2,7,2,9,2,11……,以此类推,四个同学分别得出一个结论:
A、 B、 C、 D、12. 将数按以下规律排列:1,2,3,2,5,2,7,2,9,2,11……,以此类推,四个同学分别得出一个结论:杨一:第99个数是99;
张三:第2022个数是2;
李四:前101个数的和为2652;
王五,前200个数中有7个完全平方数;
四个结论正确的有( )个
A、4 B、3 C、2 D、113. 如图,各正方形中的四个数之间都有相同的规律,根据此规律,x的值为( ) A、242 B、232 C、220 D、25214. 如图,分别用火柴棍连续搭建等边三角形和正六边形,公共边只用一根火柴棍.如果搭建等边三角形和正六边形共用了2018根火柴,并且等边三角形的个数比正六边形的个数多7,那么连续搭建的等边三角形的个数是( )
A、242 B、232 C、220 D、25214. 如图,分别用火柴棍连续搭建等边三角形和正六边形,公共边只用一根火柴棍.如果搭建等边三角形和正六边形共用了2018根火柴,并且等边三角形的个数比正六边形的个数多7,那么连续搭建的等边三角形的个数是( ) A、291 B、292 C、293 D、29415. 已知整数、、、、……满足下列条件: , , , , …,(n为正整数)依此类推,则的值为( )A、-1010 B、-2020 C、-1011 D、-202216. 如图所示,直线相交于点 , “阿基米德曲线”从点开始生成,如果将该曲线与每条射线的交点依次标记为….那么标记为“”的点在( )
A、291 B、292 C、293 D、29415. 已知整数、、、、……满足下列条件: , , , , …,(n为正整数)依此类推,则的值为( )A、-1010 B、-2020 C、-1011 D、-202216. 如图所示,直线相交于点 , “阿基米德曲线”从点开始生成,如果将该曲线与每条射线的交点依次标记为….那么标记为“”的点在( ) A、射线上 B、射线上 C、射线上 D、射线上17. 斐波那契螺旋线,也称“黄金螺旋线”,它可以通过分别以1,1,2,3,5,…为半径,依次作圆心角为90°的扇形弧线画出来(如图).第1步中扇形的半径是1cm,按如图所示的方法依次画,第8步所画扇形的弧长为( )
A、射线上 B、射线上 C、射线上 D、射线上17. 斐波那契螺旋线,也称“黄金螺旋线”,它可以通过分别以1,1,2,3,5,…为半径,依次作圆心角为90°的扇形弧线画出来(如图).第1步中扇形的半径是1cm,按如图所示的方法依次画,第8步所画扇形的弧长为( ) A、 B、 C、 D、18. 二次函数y=x2的图象如图所示,点A0 位于坐标原点,A1 , A2 , A3 , …,A2023在y轴的正半轴上,B1 , B2 , B3 , …,B2023在二次函数y=x2第一象限的图象上,若△A0B1A1 , △A1B2A2 , △A2B3A3 , …,△A2022B2023A2023都是等边三角形,则△A2022B2023A2023的周长是( )
A、 B、 C、 D、18. 二次函数y=x2的图象如图所示,点A0 位于坐标原点,A1 , A2 , A3 , …,A2023在y轴的正半轴上,B1 , B2 , B3 , …,B2023在二次函数y=x2第一象限的图象上,若△A0B1A1 , △A1B2A2 , △A2B3A3 , …,△A2022B2023A2023都是等边三角形,则△A2022B2023A2023的周长是( )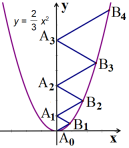 A、6069 B、6066 C、6063 D、606019. 如图,点M在线段AN的延长线上,且线段MN=20,第一次操作:分别取线段AM和AN的中点M1 , N1;第二次操作:分别取线段AM1和AN1的中点M2 , N2;第三次操作:分别取线段AM2和AN2的中点M3 , N3;…连续这样操作10次,则M10N10=( )
A、6069 B、6066 C、6063 D、606019. 如图,点M在线段AN的延长线上,且线段MN=20,第一次操作:分别取线段AM和AN的中点M1 , N1;第二次操作:分别取线段AM1和AN1的中点M2 , N2;第三次操作:分别取线段AM2和AN2的中点M3 , N3;…连续这样操作10次,则M10N10=( )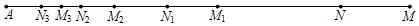 A、2 B、 C、 D、20. 如图,∠AOB=α , OA1、OB1分别是∠AOM和∠MOB的平分线,OA2、OB2分别是∠A1OM和∠MOB1的平分线,OA3、OB3分别是∠A2OM和∠MOB2的平分线,…,OAn、分别是∠An-1OM和∠MOBn-1的平分线,则∠AnOBn的度数是( )
A、2 B、 C、 D、20. 如图,∠AOB=α , OA1、OB1分别是∠AOM和∠MOB的平分线,OA2、OB2分别是∠A1OM和∠MOB1的平分线,OA3、OB3分别是∠A2OM和∠MOB2的平分线,…,OAn、分别是∠An-1OM和∠MOBn-1的平分线,则∠AnOBn的度数是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
21. 若一个正整数能表示为两个正整数的平方差,则称这个正整数为“智慧数“(如3=22-12 , 5=32-22 , 7=42-32 , 8=32-12 , 12=42-22 , 16=52-32 , 15=42-12 , 21=52-22 , 27=62-32……),仿照上面的例子,请写出一个“智慧数”:(答案不唯一,任写一个即可)22. 2020年比较流行一款推理类游戏,是用剧本虚拟出一场故事,玩家根据演绎和推理案件过程,得出结论.类比,此游戏过程,请同学们用扑克牌做一个简单的推理游戏:
①从左到右有三张不重复的扑克牌,这三张牌中不是红桃就是方块;
②红桃右边有且仅有一张方块;
③6的左边至少有一张是8;
④8的右边至少有一张是8.
请写出这三张牌从左到右的顺序可能是: . (填写正确的序号)
①红桃8,方块6,方块8②红桃8,红桃6,方块8③红桃8,方块8,红桃6
 23. 如图,某计算装置有一数据输入口A和一运算结果的输出口B,如表是小明输入的一些数据和这些数据经该装置计算后输出的相应结果按照这个计算装置的计算规律,若输入的数是n,则输出的数是.
23. 如图,某计算装置有一数据输入口A和一运算结果的输出口B,如表是小明输入的一些数据和这些数据经该装置计算后输出的相应结果按照这个计算装置的计算规律,若输入的数是n,则输出的数是.
A 1 2 3 4 5 B 2 5 10 17 26 24. 如图,在平面直角坐标系中,点A1(1,0)、A2(3,0)、A3(6,0)、A4(10,0)、……,以A1A2为对角线作第一个正方形A1C1A2B1 , 以A2A3为对角线作第二个正方形A2C2A3B2 , 以A3A4 , 为对角线作第三个正方形A3C3A4B3 , ……,顶点B1 , B2 , B3……都在第一象限,按照此规律依次下去,则点Bn的坐标为.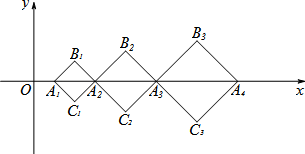 25. 如图所示的几何体都是由棱长为1个单位的正方体摆成的,经计算可得第①个几何体的表面积为6个平方单位,第②个几何体的表面积为18个平方单位,第③个几何体的表面积是36个平方单位,…依此规律,则第⑩个几何体的表面积是个平方单位.
25. 如图所示的几何体都是由棱长为1个单位的正方体摆成的,经计算可得第①个几何体的表面积为6个平方单位,第②个几何体的表面积为18个平方单位,第③个几何体的表面积是36个平方单位,…依此规律,则第⑩个几何体的表面积是个平方单位.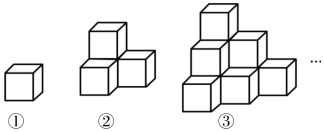 26. 一根绳子弯曲成如图1所示的形状.当用剪刀像图2那样沿虚线a把绳子剪断时,绳子被剪为5段;当用剪刀像图3那样沿虚线b(b∥a)把绳子再剪一次时,绳子就被剪为9段.若用剪刀在虚线a,b之间把绳子再剪(n﹣2)次(剪刀的方向与a平行),这样一共剪n次时绳子的段数是.
26. 一根绳子弯曲成如图1所示的形状.当用剪刀像图2那样沿虚线a把绳子剪断时,绳子被剪为5段;当用剪刀像图3那样沿虚线b(b∥a)把绳子再剪一次时,绳子就被剪为9段.若用剪刀在虚线a,b之间把绳子再剪(n﹣2)次(剪刀的方向与a平行),这样一共剪n次时绳子的段数是. 27. 观察下列各式:
27. 观察下列各式:,
,
,
……
请利用你发现的规律,计算:
其结果为
28. 如图,已知△P1OA1 , △P2A1A2 , △P3A2A3…△PnAn﹣1An都是等腰直角三角形,点P1、P2、P3…Pn都在函数y=(x>0)的图象上,斜边OA1、A1A2、A2A3…An﹣1An都在x轴上.则点A2021的坐标为 . 29. 如图,已知正方形ABCD的边长为2,在BC的延长线上取点B1 , 使∠CB1D=60°,分别过点D,B1作DB1 , BC的垂线,两垂线交于点A1 , 再以A1B1为边向右侧作正方形A1B1C1D1;在BC1的延长线上取点B2 , 使∠C1B2D1=60°,分别过点D1 , B2作D1B2 , BC1的垂线,两垂线交于点A2 , 再以A2B2为边向右侧作正方形A2B2C2D2;……,按此规律继续作下去,则正方形A2022B2022C2022D2022的面积为 .
29. 如图,已知正方形ABCD的边长为2,在BC的延长线上取点B1 , 使∠CB1D=60°,分别过点D,B1作DB1 , BC的垂线,两垂线交于点A1 , 再以A1B1为边向右侧作正方形A1B1C1D1;在BC1的延长线上取点B2 , 使∠C1B2D1=60°,分别过点D1 , B2作D1B2 , BC1的垂线,两垂线交于点A2 , 再以A2B2为边向右侧作正方形A2B2C2D2;……,按此规律继续作下去,则正方形A2022B2022C2022D2022的面积为 . 30. 如图,将一个边长为3的正方形纸片进行分割,部分①的面积是边长为3的正方形纸片的一半,部分②的面积是部分①的一半,部分③的面积是部分②的一半,以此类推,n部分的面积是 . (用含n的式子表示)
30. 如图,将一个边长为3的正方形纸片进行分割,部分①的面积是边长为3的正方形纸片的一半,部分②的面积是部分①的一半,部分③的面积是部分②的一半,以此类推,n部分的面积是 . (用含n的式子表示)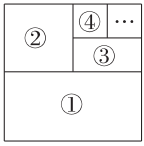
三、计算题
-
31.32. 在进行二次根式化简时,我们有时会碰上如 一样的式子,其实我们还可以将其进一步化简: ①, ②, ③.以上这种化简的步骤叫做分母有理化.
还可以用以下方法化简:
④.
(1)、请用上面介绍的两种不同方法化简 .(2)、试用上述方法化简: .四、解答题
-
33. 图1中,有一个平行四边形;
图2中,由2个相同的平行四边形拼成一排的图形,这图形中可以找到3个平行四边形;
图3中,由3个相同的平行四边形拼成一排的图形,这图形中可以找到6个平行四边形;

由此我们可以提出一个这样的问题:
图4中,由4个相同的平行四边形拼成一排的图形中,可以找到几个平行四边形?
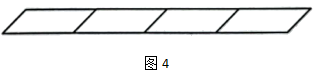
答:10个
请你根据以上事实,将一些相同的平行四边形横向或纵向拼接,由此提出一个数学问题,并写出答案.
34. 如图所示,由一些点组成形如三角形的图形,每条“边”(包括两个顶点)有 个点,每个图形的总点数记为S . (1)、当 时,S的值为;当 时,S的值为;(2)、每条“边”有n个点时的总点数S是(用含n的式子表示);(3)、当 时,总点数S是多少?35. 我们知道,有理数包括整数、有限小数和无限循环小数,事实上,所有的有理数都可以化为分数形式(整数可看作分母为1的分数),那么无限循环小数如何表示为分数形式呢?请看以下示例:
(1)、当 时,S的值为;当 时,S的值为;(2)、每条“边”有n个点时的总点数S是(用含n的式子表示);(3)、当 时,总点数S是多少?35. 我们知道,有理数包括整数、有限小数和无限循环小数,事实上,所有的有理数都可以化为分数形式(整数可看作分母为1的分数),那么无限循环小数如何表示为分数形式呢?请看以下示例:例:将 化为分数形式,
由于 ,设 ,①
得 ,②
②−①得 ,解得 ,于是得 .
同理可得 , .
根据以上阅读,回答下列问题:(以下计算结果均用最简分数表示)
(类比应用)
(1)、 ;(2)、将 化为分数形式,写出推导过程;(3)、(迁移提升), ;(注 , )
(4)、(拓展发现)若已知 ,则 .
36. (阅读材料)观察下列图形与等式的关系,并填空: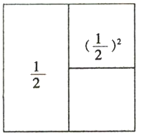 ⇒ +( )2=1﹣( )2;
⇒ +( )2=1﹣( )2;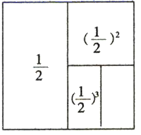 ⇒ +( )2+( )3=
⇒ +( )2+( )3=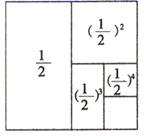 ⇒ +( )2+( )3+( )4=
⇒ +( )2+( )3+( )4=(规律探究)观察下图:

根据以上发现,用含n的代数式填空: +( )2+( )3+( )4+( )5+…+( )n= .
(解决问题)根据以上发现,计算: = .
37. 如下图,将一张正方形纸片,剪成四个大小形状一样的小正方形,然后将其中的一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去; (1)、填表:
(1)、填表:剪的次数
1
2
3
4
5
正方形个数
(2)、如果剪了100次,共剪出多少个小正方形?(3)、如果剪了n次,共剪出多少个小正方形?(4)、观察图形,你还能得出什么规律?38. 如图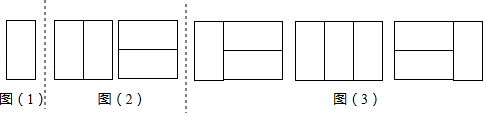
(问题)用n个2×1矩形,镶嵌一个2×n矩形,有多少种不同的镶嵌方案?(2×n矩形表示矩形的邻边是2和n)
(探究)不妨假设有an种不同的镶嵌方案.为探究an的变化规律,我们采取一般问题特殊化的策略,先从最简单情形入手,再逐次递进,最后猜想得出结论.
探究一:用1个2×1矩形,镶嵌一个2×1矩形,有多少种不同的镶嵌方案?
如图(1),显然只有1种镶嵌方案.所以,a1=1.
探究二:用2个2×1矩形,镶嵌一个2×2矩形,有多少种不同的镶嵌方案?
如图(2),显然只有2种镶嵌方案.所以,a2=2.
探究三:用3个2×1矩形,镶嵌一个2×3矩形,有多少种不同的镶嵌方案?
一类:在探究一每个镶嵌图的右侧再横着镶嵌2个2×1矩形,有1种镶嵌方案;
二类:在探究二每个镶嵌图的右侧再竖着镶嵌1个2×1矩形,有2种镶嵌方案;
如图(3).所以,a3=1+2=3.
(1)、探究四:用4个2×1矩形,镶嵌一个2×4矩形,有多少种不同的镶嵌方案?一类:在探究二每个镶嵌图的右侧再横着镶嵌2个2×1矩形,有 种镶嵌方案;
二类:在探究三每个镶嵌图的右侧再竖着镶嵌1个2×1矩形,有 种镶嵌方案;
所以,a4= .
(2)、探究五:用5个2×1矩形,镶嵌一个2×5矩形,有多少种不同的镶嵌方案?(仿照上述方法,写出探究过程,不用画图)
……
(结论)用n个2×1矩形,镶嵌一个2×n矩形,有多少种不同的镶嵌方案?
(直接写出an与an﹣1 , an﹣2的关系式,不写解答过程).
(应用)用10个2×1矩形,镶嵌一个2×10矩形,有 ▲ 种不同的镶嵌方案.
39. 问题的提出:n个平面最多可以把空间分割成多少个部分?问题的转化:由n上面问题比较复杂,所以我们先来研究跟它类似的一个较简单的问题:
n条直线最多可以把平面分割成多少个部分?
如图1,很明显,平面中画出1条直线时,会得到1+1=2个部分;所以,1条直线最多可以把平面分割成2个部分;
如图2,平面中画出第2条直线时,新增的一条直线与已知的1条直线最多有1个交点,这个交点会把新增的这条直线分成2部分,从而多出2个部分,即总共会得到1+1+2=4个部分,所以,2条直线最多可以把平面分割成4个部分;
如图3,平面中画出第3条直线时,新增的一条直线与已知的2条直线最多有2个交点,这2个交点会把新增的这条直线分成3部分,从而多出3个部分,即总共会得到1+1+2+3=7个部分,所以,3条直线最多可以把平面分割成7个部分;
平面中画出第4条直线时,新增的一条直线与已知的3条直线最多有3个交点,这3个交点会把新增的这条直线分成4部分,从而多出4个部分,即总共会得到1+1+2+3+4=11个部分,所以,4条直线最多可以把平面分割成11个部分;…

①请你仿照前面的推导过程,写出“5条直线最多可以把平面分割成多少个部分”的推导过程(只写推导过程,不画图);
②根据递推规律用n的代数式填空:n条直线最多可以把平面分割成几个部分.
问题的解决:借助前面的研究,我们继续开头的问题;n个平面最多可以把空间分割成多少个部分?
首先,很明显,空间中画出1个平面时,会得到1+1=2个部分;所以,1个平面最多可以把空间分割成2个部分;
空间中有2个平面时,新增的一个平面与已知的1个平面最多有1条交线,这1条交线会把新增的这个平面最多分成2部分,从而多出2个部分,即总共会得到1+1+2=4个部分,所以,2个平面最多可以把空间分割成4个部分;
空间中有3个平面时,新增的一个平面与已知的2个平面最多有2条交线,这2条交线会把新增的这个平面最多分成4部分,从而多出4个部分,即总共会得到1+1+2+4=8个部分,所以,3个平面最多可以把空间分割成8个部分;
空间中有4个平面时,新增的一个平面与已知的3个平面最多有3条交线,这3条交线会把新增的这个平面最多分成7部分,从而多出7个部分,即总共会得到1+1+2+4+7=15个部分,所以,4个平面最多可以把空间分割成15个部分;
空间中有5个平面时,新增的一个平面与已知的4个平面最多有4条交线,这4条交线会把新增的这个平面最多分成11部分,而从多出11个部分,即总共会得到1+1+2+4+7+11=26个部分,所以,5个平面最多可以把空间分割成26个部分;…
③请你仿照前面的推导过程,写出“6个平面最多可以把空间分割成多少个部分?”的推导过程(只写推导过程,不画图);
④根据递推规律填写结果:10个平面最多可以把空间分割成几个部分;
⑤设n个平面最多可以把空间分割成Sn个部分,设n-1个平面最多可以把空间分割成Sn−1个部分,前面的递推规律可以用Sn−1和n的代数式表示Sn;这个等式是Sn等于多少.
40. (问题)用n边形的对角线把n边形分割成(n-2个三角形,共有多少种不同的分割方案 ?(探究)为了解决上面的数学问题,我们采取一般问题特殊化的策略,先从最简单情形入手,再逐次递进转化,最后猜想得出结论.不妨假设n边形的分割方案有 种.
探究一:用四边形的对角线把四边形分割成2个三角形,共有多少种不同的分割方案?如图①,图②,显然,只有2种不同的分割方案.所以, .


探究二:用五边形的对角线把五边形分割成3个三角形,共有多少种不同的分割方案?不妨把分割方案分成三类:



第1类:如图③,用点 , 与 连接,先把五边形分割转化成1个三角形和1个四边形,再把四边形分割成2个三角形,由探究一知,有 种不同的分割方案,所以,此类共有 种不同的分割方案.
第2类:如图④,用点 , 与 连接,把五边形分割成3个三角形,有1种不同的分割方案,可视为 种分割方案.
第3类:如图⑤,用点 , 与 连接,先把五边形分割转化成1个三角形和1个四边形,再把四边形分割成2个三角形,由探究一知,有f(4)种不同的分割方案,所以,此类共有f(4)种不同的分割方案.
所以, (种)
探究三:用六边形的对角线把六边形分割成4个三角形,共有多少种不同的分割方案?不妨把分割方案分成四类:
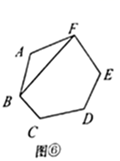
第1类:如图⑥,用 , 与 连接,先把六边形分割转化成1个三角形和1个五边形,再把五边形分割成3个三角形,由探究二知,有 种不同的分割方案,所以,此类共有 种不同的分割方案.
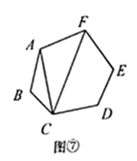
第2类:如图⑦,用 , 与 连接,先把六边形分割转化成2个三角形和1个四边形.再把四边形分割成2个三角形,由探究一知,有 种不同的分割方案.所以,此类共有 种分割方案.
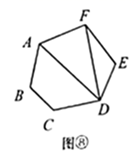
第3类:如图⑧,用 , 与 连接,先把六边形分割转化成2个三角形和1个四边形.再把四边形分割成2个三角形,由探究一知,有 种不同的分割方案.所以,此类共有 种分割方案.
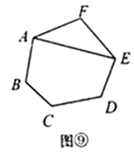
第4类:如图,用 , 与 连接,先把六边形分割转化成1个三角形和1个五边形,再把五边形分割成3个三角形,由探究二知,有 种不同的分割方案.所以,此类共有 种分割方案.
所以,
(种)
探究四:用七边形的对角线把七边形分割成5个三角形,则 与 的关系为 ,共有种不同的分割方案.
……
(结论)用 边形的对角线把 边形分割成 个三角形,共有多少种不同的分割方案 ?(直接写出 与 之间的关系式,不写解答过程)
(应用)用九边形的对角线把九边形分割成7个三角形,共有多少种不同的分割方案?(应用上述结论中的关系式求解)