2022年中考数学二轮专题复习-图像的变换
试卷更新日期:2022-04-17 类型:二轮复习
一、单选题
-
1. 把抛物线y=2x2向下平移1个单位,则平移后抛物线的解析式为( )A、y=2x2 + 1 B、y=2x2-1 C、y= D、y=2. 如图,有一条直的宽纸带,按图折叠,则∠α的度数等于( )
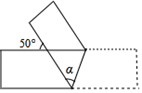 A、50° B、65° C、75° D、80°3. 如图,在平面直角坐标系中,将 OAB以原点O为位似中心放大后得到 OCD,若B(0,1),D(0,3),则 OAB与 OCD的面积比是( )
A、50° B、65° C、75° D、80°3. 如图,在平面直角坐标系中,将 OAB以原点O为位似中心放大后得到 OCD,若B(0,1),D(0,3),则 OAB与 OCD的面积比是( ) A、2:1 B、1:3 C、1:9 D、9:14. 抛物线y=﹣2x2经过平移得到y=﹣2(x-1)2+5,平移方法是( )A、向左平移1个单位,再向下平移5个单位 B、向左平移1个单位,再向下平移5个单位 C、向右平移1个单位,再向下平移5个单位 D、向右平移1个单位,再向上平移5个单位5. 有一张矩形纸片 , , , 将纸片折叠使边落在边上,折痕为 , 再将以为折痕向右折叠,与交于点(如下图),则的长为( )
A、2:1 B、1:3 C、1:9 D、9:14. 抛物线y=﹣2x2经过平移得到y=﹣2(x-1)2+5,平移方法是( )A、向左平移1个单位,再向下平移5个单位 B、向左平移1个单位,再向下平移5个单位 C、向右平移1个单位,再向下平移5个单位 D、向右平移1个单位,再向上平移5个单位5. 有一张矩形纸片 , , , 将纸片折叠使边落在边上,折痕为 , 再将以为折痕向右折叠,与交于点(如下图),则的长为( )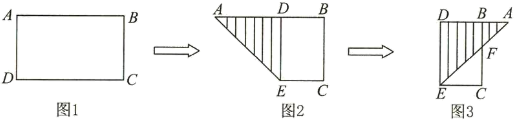 A、0.5 B、0.75 C、1 D、1.256. 如图,已知点D,E,F分别在△ABC的三边上,将△ABC沿DE,DF翻折,顶点B,C均落在△ABC内的点O处,且BD与CD重合于线段OD,若∠AEO+∠AFO=58°,则∠A的度数为( )
A、0.5 B、0.75 C、1 D、1.256. 如图,已知点D,E,F分别在△ABC的三边上,将△ABC沿DE,DF翻折,顶点B,C均落在△ABC内的点O处,且BD与CD重合于线段OD,若∠AEO+∠AFO=58°,则∠A的度数为( )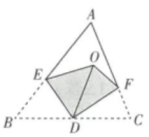 A、58° B、59° C、60° D、61°7. 直线 与y轴交于点A,与x轴交于点B,直线 与直线 关于x轴对称且过点(2,-1),则△ABO的面积为( )A、8 B、1 C、2 D、48. 如图,将长、宽分别为6cm, cm的长方形纸片分别沿AB,AC折叠,点M,N恰好重合于点P.若∠α=60°,则折叠后的图案(阴影部分)面积为( )
A、58° B、59° C、60° D、61°7. 直线 与y轴交于点A,与x轴交于点B,直线 与直线 关于x轴对称且过点(2,-1),则△ABO的面积为( )A、8 B、1 C、2 D、48. 如图,将长、宽分别为6cm, cm的长方形纸片分别沿AB,AC折叠,点M,N恰好重合于点P.若∠α=60°,则折叠后的图案(阴影部分)面积为( )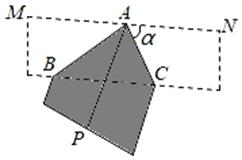 A、 cm2 B、(36 )cm2 C、 cm2 D、 cm29. 如图,直角三角形纸片ABC中,∠ACB=90°,∠A=50°,将其沿边AB上的中线CE折叠,使点A落在点 处,则∠ EB的度数为( )
A、 cm2 B、(36 )cm2 C、 cm2 D、 cm29. 如图,直角三角形纸片ABC中,∠ACB=90°,∠A=50°,将其沿边AB上的中线CE折叠,使点A落在点 处,则∠ EB的度数为( )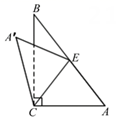 A、10° B、15° C、20° D、40°10. 如图所示,平行四边形纸片ABCD中,∠A=120°,AB=4,BC=5,剪掉两个角后,得到六边形AEFCGH,它的每个内角都是120°,且EF=1,HG=2,则这个六边形的周长为( )
A、10° B、15° C、20° D、40°10. 如图所示,平行四边形纸片ABCD中,∠A=120°,AB=4,BC=5,剪掉两个角后,得到六边形AEFCGH,它的每个内角都是120°,且EF=1,HG=2,则这个六边形的周长为( )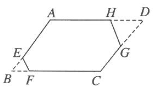 A、12 B、15 C、16 D、1811. 将二次函数 的图象沿x轴向左平移2个单位长度,再沿y轴向上平移3个单位长度,得到的函数表达式是( )A、 B、 C、 D、12. 如图,在平面直角坐标系中,将函数y=x2-2x的图象先沿x轴翻折,再向上平移5个单位长度,得到的抛物线所对应的函数表达式是( )
A、12 B、15 C、16 D、1811. 将二次函数 的图象沿x轴向左平移2个单位长度,再沿y轴向上平移3个单位长度,得到的函数表达式是( )A、 B、 C、 D、12. 如图,在平面直角坐标系中,将函数y=x2-2x的图象先沿x轴翻折,再向上平移5个单位长度,得到的抛物线所对应的函数表达式是( ) A、 B、 C、 D、13. 如图,矩形ABCD中,AB=1,BC= , 点P为CD边上的一个动点,连接AP,将四边形ABCP沿AP折叠至四边形AB'C'P,在点P由点C运动到点D的过程中,点C'运动的路径长为( )
A、 B、 C、 D、13. 如图,矩形ABCD中,AB=1,BC= , 点P为CD边上的一个动点,连接AP,将四边形ABCP沿AP折叠至四边形AB'C'P,在点P由点C运动到点D的过程中,点C'运动的路径长为( ) A、 B、 C、 D、14. 如图,将函数y(x+4)2+5的图象沿y轴向下平移得到一条新函数的图象,其中点A(﹣6,m),B(﹣1,n)平移后的对应点分别为点A'、B',若曲线AB扫过的面积为30(图中的阴影部分),则新图象的函数表达式是( )
A、 B、 C、 D、14. 如图,将函数y(x+4)2+5的图象沿y轴向下平移得到一条新函数的图象,其中点A(﹣6,m),B(﹣1,n)平移后的对应点分别为点A'、B',若曲线AB扫过的面积为30(图中的阴影部分),则新图象的函数表达式是( ) A、y(x+4)2﹣2 B、y(x+4)2﹣1 C、y(x+4)2+2 D、y(x+4)2+115. 如图,在平面直角坐标系中,直线AB与x轴交于点A(﹣2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线(k≠0)上,则k的值为( )
A、y(x+4)2﹣2 B、y(x+4)2﹣1 C、y(x+4)2+2 D、y(x+4)2+115. 如图,在平面直角坐标系中,直线AB与x轴交于点A(﹣2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线(k≠0)上,则k的值为( )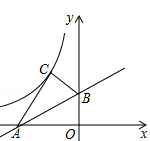 A、4 B、﹣2 C、 D、16. 如图,在Rt△ABC中, , ,把 折叠,使 落在 上,点 与 上的点 重合,展开后,折痕 交 于点 ,连接 、 , 交 于 点.下列结论:① ②若将 沿 折叠,则点 一定落在 上③图中有7个等腰三角形④若 ,则 ⑤ ,上述结论中正确的个数是( )
A、4 B、﹣2 C、 D、16. 如图,在Rt△ABC中, , ,把 折叠,使 落在 上,点 与 上的点 重合,展开后,折痕 交 于点 ,连接 、 , 交 于 点.下列结论:① ②若将 沿 折叠,则点 一定落在 上③图中有7个等腰三角形④若 ,则 ⑤ ,上述结论中正确的个数是( )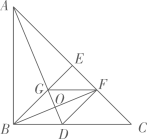 A、2个 B、3个 C、4个 D、5个17. 如图,将一个等腰直角三角形△ABC按如图方式折叠,若DE=a,DC=b,下列四个结论:①DC′平分∠BDE;②BC长为2a+b;③△BDC′是等腰三角形;④△CED的周长等于BC的长.其中,正确的是( )
A、2个 B、3个 C、4个 D、5个17. 如图,将一个等腰直角三角形△ABC按如图方式折叠,若DE=a,DC=b,下列四个结论:①DC′平分∠BDE;②BC长为2a+b;③△BDC′是等腰三角形;④△CED的周长等于BC的长.其中,正确的是( ) A、①②④ B、②③④ C、②③ D、②④18. 矩形ABCD中,AB=12,BC=8,将矩形沿MN折叠,使点C恰好落在AD边的中点F处,以矩形对称中心O点为圆心的圆与FN相切于点G,则⊙O的半径为( )
A、①②④ B、②③④ C、②③ D、②④18. 矩形ABCD中,AB=12,BC=8,将矩形沿MN折叠,使点C恰好落在AD边的中点F处,以矩形对称中心O点为圆心的圆与FN相切于点G,则⊙O的半径为( )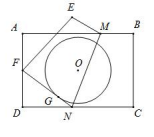 A、3.6 B、 C、3.5 D、19. 如图,在 中, 是 延长线上一点, 是边 上一动点, 连结 ,作 与 关于 对称 (点 与点 对应),连结 ,则 长的最小值是( )
A、3.6 B、 C、3.5 D、19. 如图,在 中, 是 延长线上一点, 是边 上一动点, 连结 ,作 与 关于 对称 (点 与点 对应),连结 ,则 长的最小值是( )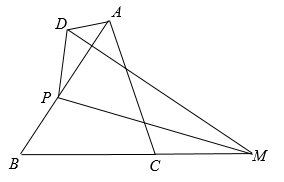 A、0.5 B、0.6 C、 D、20. 将二次函数y=﹣x2+2x+3的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线y=x+b与新函数的图象恰有3个公共点时,b的值为( )
A、0.5 B、0.6 C、 D、20. 将二次函数y=﹣x2+2x+3的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线y=x+b与新函数的图象恰有3个公共点时,b的值为( )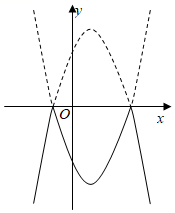 A、 或﹣2 B、 或﹣2 C、 或﹣3 D、 或﹣3
A、 或﹣2 B、 或﹣2 C、 或﹣3 D、 或﹣3二、填空题
-
21. 将一次函数的图象沿x轴向左平移4个单位长度,所得到的图象对应的函数表达式是.22. 将抛物线y=2(x+2)2﹣5向左平移3个单位长度后,再沿x轴翻折,则变换后所得抛物线的顶点坐标为 .23. 如图,在等腰中, , .点和点分别在边和边上,连接.将沿折叠,得到 , 点恰好落在的中点处.设与交于点 , 则.
 24. 如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上OA=5;OC=4.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处.则D坐标为.
24. 如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上OA=5;OC=4.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处.则D坐标为.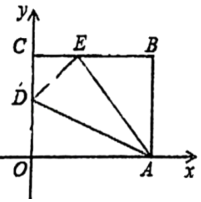 25. 如图,正六边形ABCDEF是由正六边形A′B′C′D′E′F′经过位似变换得到的,已知AB=3,B′C′=1,则正六边形A′B′C′D′E′F′和正六边形ABCDEF的面积比是 .
25. 如图,正六边形ABCDEF是由正六边形A′B′C′D′E′F′经过位似变换得到的,已知AB=3,B′C′=1,则正六边形A′B′C′D′E′F′和正六边形ABCDEF的面积比是 .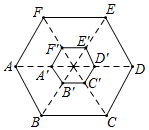 26. 如图,将三角形纸片ABC沿AD折叠,使点C落在BD边上的点E处.若BC=10,BE=2,则AB2﹣AC2的值为 .
26. 如图,将三角形纸片ABC沿AD折叠,使点C落在BD边上的点E处.若BC=10,BE=2,则AB2﹣AC2的值为 .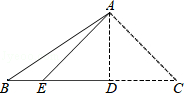 27. 在 中,D为BC中点,将 沿AD折叠,得到 ,连接EC,若已知 ,且 ,则点E到AD的距离为.
27. 在 中,D为BC中点,将 沿AD折叠,得到 ,连接EC,若已知 ,且 ,则点E到AD的距离为.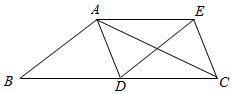 28. 小华用一张直角三角形纸片玩折纸游戏,如图1,在中, , , . 第一步,在边上找一点 , 将纸片沿折叠,点落在处,如图2,第二步,将纸片沿折叠,点落在处,如图3.当点恰好在原直角三角形纸片的边上时,线段的长为 .
28. 小华用一张直角三角形纸片玩折纸游戏,如图1,在中, , , . 第一步,在边上找一点 , 将纸片沿折叠,点落在处,如图2,第二步,将纸片沿折叠,点落在处,如图3.当点恰好在原直角三角形纸片的边上时,线段的长为 .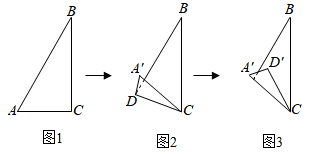 29. 如图,在矩形中,点N为边上不与B、C重合的一个动点,过点N作交于点M,交于点E,以为对称轴折叠矩形 , 点A、B的对应点分别是G、F,连接、 , 若 , , 当为直角三角形时,的长为 .
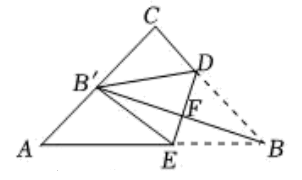
29. 如图,在矩形中,点N为边上不与B、C重合的一个动点,过点N作交于点M,交于点E,以为对称轴折叠矩形 , 点A、B的对应点分别是G、F,连接、 , 若 , , 当为直角三角形时,的长为 . 30. 如图,在平面直角坐标系中,等边△ABC与等边△BDE是以原点为位似中心的位似图形,且相似比为 , 点A、B、D在x轴上,若等边△BDE的边长为6,则点C的坐标为 .
30. 如图,在平面直角坐标系中,等边△ABC与等边△BDE是以原点为位似中心的位似图形,且相似比为 , 点A、B、D在x轴上,若等边△BDE的边长为6,则点C的坐标为 .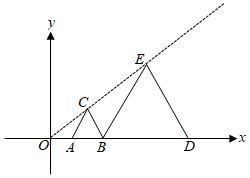
三、解答题
-
31. 如图1,已知三角形纸片ABC, , ,将其折叠,如图2,使点A与点B重合,折痕为ED,点E,D分别在AB,AC上,求 的大小.
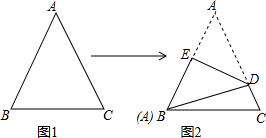 32. 如图,长方形纸片ABCD , 沿折痕AE折叠边AD , 使点D落在BC边上的F处,已知AB=6,AD=10,求EC的长
32. 如图,长方形纸片ABCD , 沿折痕AE折叠边AD , 使点D落在BC边上的F处,已知AB=6,AD=10,求EC的长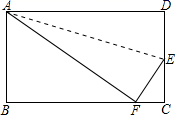 33. 如图,在边长为1的小正方形组成的网格中, 的顶点在格点(网格线的交点)上,以点 为原点建立平面直角坐标系,点 的坐标为(1,0).
33. 如图,在边长为1的小正方形组成的网格中, 的顶点在格点(网格线的交点)上,以点 为原点建立平面直角坐标系,点 的坐标为(1,0).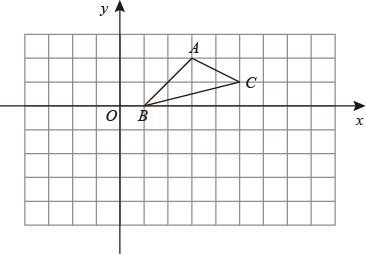
( 1 )将 向左平移5个单位长度,得到 ,画出 ;
( 2 )以点 为位似中心,将 放大到两倍(即新图与原图的相似比为2),得到 ,在所给的方格纸中画出 ;
( 3 )若点 是 的中点,经过(1)、(2)两次变换, 的对应点 的坐标是 .
34. 如图,矩形OABC中,AO=4,AB=8,点E,F分别在边AB,OC上,且AE=3,将矩形的部分沿直线EF翻折,点A的对应点A'恰好落在对角线AC上,求OF的长.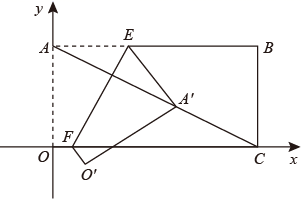 35. 已知P(2,n)为反比例函数y= (x>0)图象上的一点.将直线y=-2x沿x轴向右平移过点P时,交x轴于点Q,若点M为y轴上一个动点,求PM+QM的最小值。
35. 已知P(2,n)为反比例函数y= (x>0)图象上的一点.将直线y=-2x沿x轴向右平移过点P时,交x轴于点Q,若点M为y轴上一个动点,求PM+QM的最小值。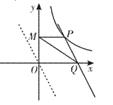 36. 矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),点D的坐标为(2,0),E为AB上的点,求当△CDE的周长最小时,点E的坐标和最小周长.
36. 矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),点D的坐标为(2,0),E为AB上的点,求当△CDE的周长最小时,点E的坐标和最小周长.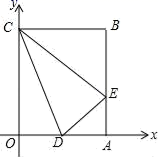 37. 如如图,将一个直角三角形纸片AOB , 放置在平面直角坐标系中,已知点O(0,0),点B在y轴的正半轴上, OA=2,∠ABO=90°,∠AOB=30°.D , E两点同时从原点O出发,D点以每秒 个单位长度的速度沿x轴正方向运动,E点以每秒1个单位长度的速度沿y轴正方向运动,连接DE , 交OA于点F , 将△OEF沿直线DE折叠得到△O′EF , 设D , E两点的运动时间为t秒.
37. 如如图,将一个直角三角形纸片AOB , 放置在平面直角坐标系中,已知点O(0,0),点B在y轴的正半轴上, OA=2,∠ABO=90°,∠AOB=30°.D , E两点同时从原点O出发,D点以每秒 个单位长度的速度沿x轴正方向运动,E点以每秒1个单位长度的速度沿y轴正方向运动,连接DE , 交OA于点F , 将△OEF沿直线DE折叠得到△O′EF , 设D , E两点的运动时间为t秒.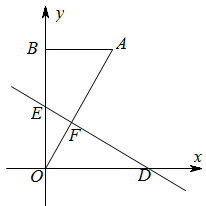 (1)、求点 的坐标及 的度数;(2)、若折叠后 与 重叠部分的面积为 ,
(1)、求点 的坐标及 的度数;(2)、若折叠后 与 重叠部分的面积为 ,①当折叠后 与 重叠部分的图形为三角形时,请写出 与 的函数关系式,并直接写出 的取值范围;
②当重叠部分面积最大时,把 绕点 旋转,得到 ,点 的对应点分别为 ,连接 ,求 面积的最大值(直接写出结果即可).
38. 已知一个等边三角形纸片 ,将该纸片放置在平面直角坐标系中, 为坐标原点,使边 与 轴的正半轴重合,点 落在第一象限,过点 作 垂直于 轴,垂足为点 .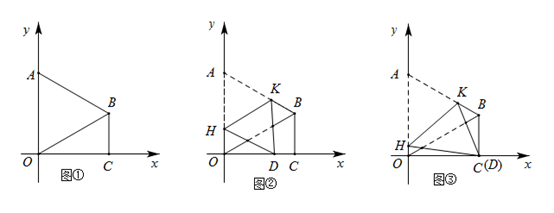
(Ⅰ)如图①,若点 坐标为 ,求 的长;
(Ⅱ)如图②,将四边形 折叠,使点 落在线段 上的点为点 , 为折痕,点 在 上,点 在 上,且使 轴.
①试判断四边形 的形状,并证明你的结论;
②求 的值;
(Ⅲ)如图③,将四边形 折叠,使点 落在线段 上的点 与 点重合, 为折痕,点 在 上,点 在 上,求 的值(直接写出结果即可).
四、综合题
-
39. 如图,在平面直角坐标系中,抛物线ybx+c与x轴交于A(﹣2,0)、B(4,0)两点(点A在点B的左侧),与y轴交于点C,连接AC、BC,点P为直线BC上方抛物线上一动点,连接OP交BC于点Q.
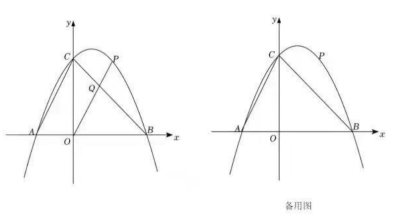 (1)、求抛物线的函数表达式;(2)、当的值最大时,求点P的坐标和的最大值;(3)、把抛物线ybx+c沿射线AC方向平移个单位得新抛物线y',M是新抛物线上一点,N是新抛物线对称轴上一点,当以M、N、B、C为顶点的四边形是平行四边形时,直接写出N点的坐标.40. 如图,已知抛物线y=ax2+bx-4与x轴交于A,B两点,与y轴交于点C,且点A的坐标为(-2,0),直线BC的解析式为y= x-4.
(1)、求抛物线的函数表达式;(2)、当的值最大时,求点P的坐标和的最大值;(3)、把抛物线ybx+c沿射线AC方向平移个单位得新抛物线y',M是新抛物线上一点,N是新抛物线对称轴上一点,当以M、N、B、C为顶点的四边形是平行四边形时,直接写出N点的坐标.40. 如图,已知抛物线y=ax2+bx-4与x轴交于A,B两点,与y轴交于点C,且点A的坐标为(-2,0),直线BC的解析式为y= x-4.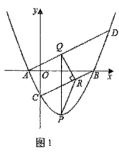
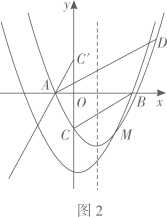 (1)、求抛物线的解析式;(2)、如图1,过点A作AD∥BC交抛物线于点D(异于点A),P是直线BC下方抛物线上一点,过点P作PQ∥y轴,交AD于点Q,过点Q作QR⊥BC于点R,连接PR.求△PQR面积的最大值及此时点P的坐标;(3)、如图2,点C关于x轴的对称点为点C′,将抛物线沿射线C′A的方向平移2 个单位长度得到新的抛物线y′,新抛物线y′与原抛物线交于点M,原抛物线的对称轴上有一动点N,平面直角坐标系内是否存在一点K,使得以D,M,N,K为顶点的四边形是矩形?若存在,请直接写出点K的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、如图1,过点A作AD∥BC交抛物线于点D(异于点A),P是直线BC下方抛物线上一点,过点P作PQ∥y轴,交AD于点Q,过点Q作QR⊥BC于点R,连接PR.求△PQR面积的最大值及此时点P的坐标;(3)、如图2,点C关于x轴的对称点为点C′,将抛物线沿射线C′A的方向平移2 个单位长度得到新的抛物线y′,新抛物线y′与原抛物线交于点M,原抛物线的对称轴上有一动点N,平面直角坐标系内是否存在一点K,使得以D,M,N,K为顶点的四边形是矩形?若存在,请直接写出点K的坐标;若不存在,请说明理由.