北师大版备考2022中考数学二轮复习专题15 一般三角形及其性质

试卷更新日期：2022-04-16 类型：二轮复习

进入出卷网下载

一、单选题

1. 已知a，b，c为△ABC三边，且满足a²c²-b²c²=a⁴-b⁴ ，则它的形状为（）

A、等边三角形 B、直角三角形 C、等腰三角形 D、等腰三角形或直角三角形

查看试题解析
2. 如图，△ABC的面积为8cm² ， AP垂直∠B的平分线BP于P，则△PBC的面积为（）

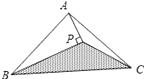A、2cm² B、3cm² C、4cm² D、5cm²

查看试题解析
3. 如图，在△ABC中，∠A=20°，∠ABC与∠ACB的角平分线交于D₁ ， ∠ABD₁与∠ACD₁的角平分线交于点D₂ ，依此类推，∠ABD₄与∠ACD₄的角平分线交于点D₅ ，则∠BD₅C的度数是（　　）

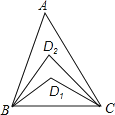A、24° B、25° C、30° D、36°

查看试题解析
4.
如图，正方形ABCD的边长为4，M在DC上，且DM=1，N是AC上一动点，则DN+MN的最小值为（）．

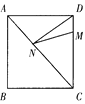A、3 B、4 C、5 D、 $4 \sqrt{2}$

查看试题解析
5.
如图，AB∥CD，∠BAC与∠DCA的平分线相交于点G，GE⊥AC于点E，F为AC上的一点，且FA=FG=FC，GH⊥CD于H．下列说法：①AG⊥CG；②∠BAG=∠CGE；③S_△_AFG=S_△_CFG；④若∠EGH：∠ECH=2：7，则∠EGF=50度．其中正确的有（　　）

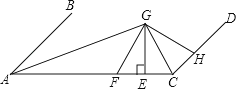A、①②③④ B、②③④ C、①③④ D、①②④

查看试题解析
6.
在矩形ABCD中，AB＝1，AD＝ $\sqrt{3}$ ，AF平分∠DAB，过C点作CE⊥BD于E，延长AF.EC交于点H，下列结论中：①AF＝FH；②BO＝BF；③CA＝CH；④BE＝3ED．正确的是（　　）

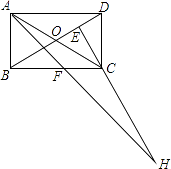A、②③ B、③④ C、①②④ D、②③④

查看试题解析
7. 如图，A，B，C分别是线段A₁B，B₁C，C₁A的中点，若△ABC的面积是1，那么△A₁B_lC₁的面积是（）

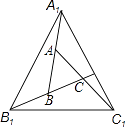A、4 B、5 C、6 D、7

查看试题解析
8. 长为1的一根绳，恰好可围成两个全等三角形，则其中一个三角形的最长边x的取值范围为（　　）

A、 $\frac{l}{6} \leq x < \frac{l}{4}$ B、 $\frac{l}{8} \leq x < \frac{l}{4}$ C、 $\frac{l}{6} < x < \frac{l}{4}$ D、 $\frac{l}{8} < x < \frac{l}{4}$

查看试题解析
9. 如图△ABC中，∠A=96°，延长BC到D，∠ABC与∠ACD的平分线相交于点A₁∠A₁BC与∠A₁CD的平分线相交于点A₂ ，依此类推，∠A₄BC与∠A₄CD的平分线相交于点A₅ ，则∠A₅的度数为（）

A、19.2° B、8° C、6° D、3°

查看试题解析
10. △ABC中，∠A、∠B、∠C的对边分别是a、b、c，下列说法中，错误的是（　　）

A、如果∠C﹣∠B=∠A，那么∠C=90° B、如果∠C=90°，那么c²﹣b²=a² C、如果（a+b）（a﹣b）=c² ，那么∠C=90° D、如果∠A=30°∠B=60°，那么AB=2BC

查看试题解析

二、填空题

11. 如图，在△ABC中，∠A=40°，∠ABC与∠ACB的平分线相交于点P，则∠BPC的度数为.

查看试题解析
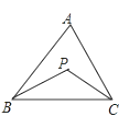12. 如图，在△ABC中，BC的垂直平分线MN交AB于点D，CD平分∠ACB.若AD＝2，BD＝3，则AC的长为.

查看试题解析
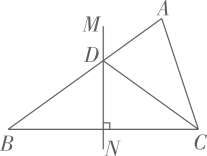13.
如图，Rt△ABC中，∠ABC＝90°，AB＝BC，直线l₁、l₂、l₃分别通过A、B、C三点，且l₁∥l₂∥l₃ ．若l₁与l₂的距离为4，l₂与l₃的距离为6，则Rt△ABC的面积为．

查看试题解析
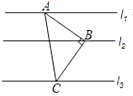14. 如图，FE∥ON，OE平分∠MON，∠FEO=28°，则∠MFE=度．

查看试题解析
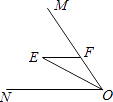15. 图1是一种折叠式晾衣架．晾衣时，该晾衣架左右晾衣臂张开后示意图如图2所示，两支脚OC＝OD＝10分米，展开角∠COD＝60°，晾衣臂OA＝OB＝10分米，晾衣臂支架HG＝FE＝6分米，且HO＝FO＝4分米．当∠AOC＝90°时，点A离地面的距离AM为分米；当OB从水平状态旋转到OB′（在CO延长线上）时，点E绕点F随之旋转至OB′上的点E′处，则B′E′﹣BE为分米．

查看试题解析
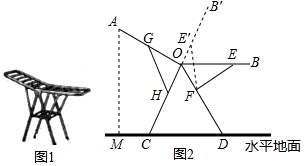16.
如图，已知双曲线 $y = \frac{k}{x} (k > 0)$ 经过Rt△OAB的斜边OB的中点D ，与直角边AB相交于点C ．当 $B C \cdot O A = 6$ 时， $k =$ ．

查看试题解析
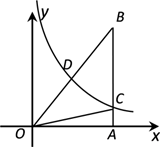17. 如图，AE⊥AB且AE＝AB，BC⊥CD且BC＝CD，请按照图中所标注的数据，计算图中阴影部分的面积S是

查看试题解析
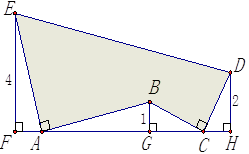18.
如图，在边长为4的正方形ABCD中，P是BC边上一动点（不含B、C两点），将△ABP沿直线AP翻折，点B落在点E处；在CD上有一点M，使得将△CMP沿直线MP翻折后，点C落在直线PE上的点F处，直线PE交CD于点N，连接MA，NA．则以下结论中正确的有（写出所有正确结论的序号）
①△CMP∽△BPA；
②四边形AMCB的面积最大值为10；
③当P为BC中点时，AE为线段NP的中垂线；
④线段AM的最小值为2 $\sqrt{5}$ ；
⑤当△ABP≌△ADN时，BP=4 $\sqrt{2}$ ﹣4．

查看试题解析

三、作图题

19. 如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A（-3，4），B（-4，1），C（-1，2）．

(1)、在图中作出△ABC关于x轴的对称图形△A₁B₁C₁；

(2)、请直接写出点C关于y轴的对称点C'的坐标：；

(3)、△ABC的面积=；

(4)、在y轴上找一点P，使得△PAC周长最小，并求出△PAC周长的最小值．

查看试题解析

四、解答题

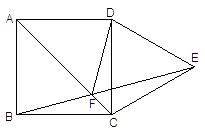
20.
正方形ABCD 的CD边长作等边△DCE，AC和BE相交于点F，连接DF.求 ∠AFD的度数.

查看试题解析
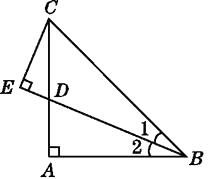
21. 如图，AB=AC，∠BAC=90°，∠1=∠2，CE⊥BE.
求证：BD=2CE.

查看试题解析

五、综合题

22.
如图，在矩形ABCD中，AB=5，AD=3，点P是AB边上一点（不与A，B重合），连接CP，过点P作PQ⊥CP交AD边于点Q，连接CQ．

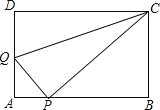(1)、当△CDQ≌△CPQ时，求AQ的长；

(2)、取CQ的中点M，连接MD，MP，若MD⊥MP，求AQ的长．

查看试题解析
23.
如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE．已知∠BAC=30°，EF⊥AB，垂足为F，连接DF．

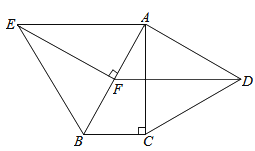(1)、试说明AC=EF；

(2)、求证：四边形ADFE是平行四边形.

查看试题解析
24. 通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的．下面是一个案例．
原题：如图①，点 $E ， F$ 分别在正方形 $A B C D$ 的边 $B C ， C D$ 上， $∠ E A F = 45 °$ ，连接 $E F$ ，则 $E F = B E + D F$ ，试说明理由．

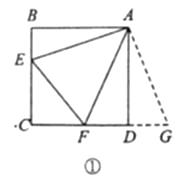(1)、思路梳理
因为 $A B = A D$ ，所以把 $Δ A B E$ 绕点 $A$ 逆时针旋转90°至 $Δ A D G$ ，可使 $A B$ 与 $A D$ 重合．因为 $∠ A D C = ∠ B = 90 °$ ，所以 $∠ F D G = 180 °$ ，点 $F ， D ， G$ 共线．
根据，易证 $Δ A F G ≅$ ，得 $E F = B E + D F$ .请证明．

(2)、类比引申
如图②，四边形 $A B C D$ 中， $A B = A D$ ， $∠ B A D = 90 °$ ，点 $E ， F$ 分别在边 $B C ， C D$ 上， $∠ E A F = 45 °$ .若 $∠ B ， ∠ D$ 都不是直角，则当 $∠ B$ 与 $∠ D$ 满足等量关系时， $E F = B E + D F$ 仍然成立，请证明．

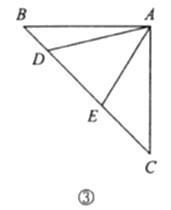
(3)、联想拓展
如图③，在 $Δ A B C$ 中， $∠ B A C = 90 ° ， A B = A C$ ，点 $D ， E$ 均在边 $B C$ 上，且 $∠ D A E = 45 °$ .猜想 $B D ， D E ， E C$ 应满足的等量关系，并写出证明过程．

查看试题解析
25.
如图1，直线MN与直线AB、CD分别交于点E、F，∠1与∠2互补．

(1)、试判断直线AB与直线CD的位置关系，并说明理由；

(2)、如图2，∠BEF与∠EFD的角平分线交于点P，EP与CD交于点G，点H是MN上一点，且GH⊥EG，求证：PF∥GH；

(3)、如图3，在（2）的条件下，连接PH，K是GH上一点使∠PHK=∠HPK，作PQ平分∠EPK，问∠HPQ的大小是否发生变化？若不变，请求出其值；若变化，说明理由．

查看试题解析