2022年中考数学二轮专题复习-与圆有关的位置关系
试卷更新日期:2022-04-15 类型:二轮复习
一、单选题
-
1. 若⊙O的半径为5cm,点A到圆心O的距离为4cm,则点A与⊙O的位置关系是( )A、点A在圆外 B、点A在圆上 C、点A在圆内 D、不能确定2. 在△ABC中, , 点O为AB中点.以点C为圆心,CO长为半径作⊙C,则⊙C 与AB的位置关系是( )
 A、相交 B、相切 C、相离 D、不确定3. 如图,若的半径为6,圆心O到一条直线的距离为3,则这条直线可能是( )
A、相交 B、相切 C、相离 D、不确定3. 如图,若的半径为6,圆心O到一条直线的距离为3,则这条直线可能是( ) A、 B、 C、 D、4. 下列语句中,正确的有( )
A、 B、 C、 D、4. 下列语句中,正确的有( )①相等的圆心角所对的弧相等;
②等弦对等弧;
③若两个相似多边形的面积比为16:9,那么这两个相似多边形的周长比是4:3;
④已知线段AB=2,点C是AB的黄全分割点,则;
⑤三角形的外心到三角形的三边距离相等.
A、1个 B、2个 C、3个 D、4个5. 已知:如图,⊙O是△ABC的外接圆,⊙O的直径为10,过点C作⊙O的切线交AB延长线于点P.BC=6,则B到CP的距离为( ) A、 B、3 C、 D、6. 如图,⊙O的半径为2,点C是圆上的一个动点,CA⊥x轴,CB⊥y轴,垂足分别为A、B,D是AB的中点,如果点C在圆上运动一周,那么点D运动过的路程长为( )
A、 B、3 C、 D、6. 如图,⊙O的半径为2,点C是圆上的一个动点,CA⊥x轴,CB⊥y轴,垂足分别为A、B,D是AB的中点,如果点C在圆上运动一周,那么点D运动过的路程长为( )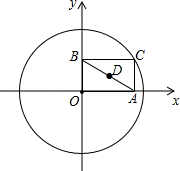 A、 B、 C、π D、2π7. 如图, 中, 于点D,点P为 上的点,
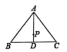
A、 B、 C、π D、2π7. 如图, 中, 于点D,点P为 上的点,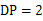 ,以点P为圆心 为半径画圆,下列说法错误的是( )
,以点P为圆心 为半径画圆,下列说法错误的是( )
 A、点A在 外 B、点B在 外 C、点C在 外 D、点D在 内8. 如图,在平面直角坐标系xOy中,点A(0,3),点B(2,1),点C(2,-3).则经画图操作可知:△ABC的外接圆的圆心坐标是( )
A、点A在 外 B、点B在 外 C、点C在 外 D、点D在 内8. 如图,在平面直角坐标系xOy中,点A(0,3),点B(2,1),点C(2,-3).则经画图操作可知:△ABC的外接圆的圆心坐标是( )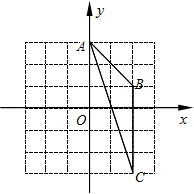 A、(-2,-1) B、(-1,0) C、(-1,-1) D、(0,-1)9. 如图,两个等圆⊙O1和⊙O2相交于A、B两点,且⊙O1经过⊙O2的圆心,则∠O1AB的度数为( )
A、(-2,-1) B、(-1,0) C、(-1,-1) D、(0,-1)9. 如图,两个等圆⊙O1和⊙O2相交于A、B两点,且⊙O1经过⊙O2的圆心,则∠O1AB的度数为( ) A、45° B、30° C、20° D、15°10. 已知直径分别为6和10的两圆没有公共点,那么这两个圆的圆心距的取值范围是( )A、d>2 B、d>8 C、d>8或0≤d<2 D、2≤d<811. A、B、C表示三个村庄,AB=1000米,BC=600米,AC=800米,为拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )A、AB中点 B、BC中点 C、AC中点 D、∠C的平分线与AB的交点12. 已知矩形ABCD的边AB=15,BC=20,以点B为圆心作圆,使A,C,D三点至少有一点在⊙B内,且至少有一点在⊙B外,则⊙B的半径r的取值范围是( ).A、r>15 B、15<r<20 C、15<r<25 D、20<r<2513. 如图,在Rt 中,OA=OB=4 ,⊙O的半径为2, 点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ长的最小值为( )
A、45° B、30° C、20° D、15°10. 已知直径分别为6和10的两圆没有公共点,那么这两个圆的圆心距的取值范围是( )A、d>2 B、d>8 C、d>8或0≤d<2 D、2≤d<811. A、B、C表示三个村庄,AB=1000米,BC=600米,AC=800米,为拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )A、AB中点 B、BC中点 C、AC中点 D、∠C的平分线与AB的交点12. 已知矩形ABCD的边AB=15,BC=20,以点B为圆心作圆,使A,C,D三点至少有一点在⊙B内,且至少有一点在⊙B外,则⊙B的半径r的取值范围是( ).A、r>15 B、15<r<20 C、15<r<25 D、20<r<2513. 如图,在Rt 中,OA=OB=4 ,⊙O的半径为2, 点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ长的最小值为( )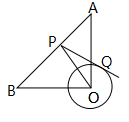 A、2 B、 C、1 D、214. 如图, 中, 于点 是半径为2的 上一动点, 连结 , 若 是 的中点, 连结 , 则 长的最大值为 ( )
A、2 B、 C、1 D、214. 如图, 中, 于点 是半径为2的 上一动点, 连结 , 若 是 的中点, 连结 , 则 长的最大值为 ( ) A、3 B、305 C、4 D、4.515. 如图,在平面直角坐标系中,P是直线y=2上的一个动点,⊙P的半径为1,直线OQ切⊙P于点Q,则线段OQ的最小值为( )
A、3 B、305 C、4 D、4.515. 如图,在平面直角坐标系中,P是直线y=2上的一个动点,⊙P的半径为1,直线OQ切⊙P于点Q,则线段OQ的最小值为( ) A、1 B、2 C、 D、16. 如图, 中, 于点 是半径为2的上一动点, 连结 , 若是的中点, 连结 , 则长的最大值为 ( )
A、1 B、2 C、 D、16. 如图, 中, 于点 是半径为2的上一动点, 连结 , 若是的中点, 连结 , 则长的最大值为 ( ) A、3 B、 C、4 D、17. 如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为斜边向外作等腰直角三角形△ACD,△BCE,弧AC和弧BC的中点分别是M,N.连接DM,EN,若C在半圆上由点A向B移动的过程中,DM∶EN的值的变化情况是( )
A、3 B、 C、4 D、17. 如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为斜边向外作等腰直角三角形△ACD,△BCE,弧AC和弧BC的中点分别是M,N.连接DM,EN,若C在半圆上由点A向B移动的过程中,DM∶EN的值的变化情况是( ) A、变大 B、变小 C、先变大再变小 D、保持不变18. 如图,在 中, , , ,以边 的中点 为圆心,作半圆与 相切,点 , 分别是边 和半圆上的动点,连接 ,则 长的最大值与最小值的和是( )
A、变大 B、变小 C、先变大再变小 D、保持不变18. 如图,在 中, , , ,以边 的中点 为圆心,作半圆与 相切,点 , 分别是边 和半圆上的动点,连接 ,则 长的最大值与最小值的和是( ) A、6 B、 C、 D、919. 如图,A(12,0),B(0,9)分别是平面直解坐标系xOy坐标轴上的点,经过点O且与AB相切的动圆与x轴、y轴分别相交于点P、Q,则线段PQ长度的最小值是( )
A、6 B、 C、 D、919. 如图,A(12,0),B(0,9)分别是平面直解坐标系xOy坐标轴上的点,经过点O且与AB相切的动圆与x轴、y轴分别相交于点P、Q,则线段PQ长度的最小值是( )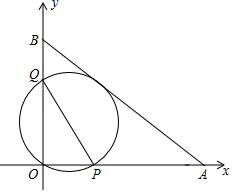 A、 B、10 C、7.2 D、20. 如图,▱ABCD中, , , , 是边AB上的两点,半径为2的 过点A,半径为1的 过点 、E、F分别是边CD, 和 上的动点 则 的最小值等于
A、 B、10 C、7.2 D、20. 如图,▱ABCD中, , , , 是边AB上的两点,半径为2的 过点A,半径为1的 过点 、E、F分别是边CD, 和 上的动点 则 的最小值等于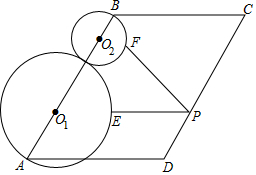 A、 B、6 C、 D、9
A、 B、6 C、 D、9二、填空题
-
21. 已知⊙A的半径为5,圆心A(4,3),坐标原点O与⊙A的位置关系是 .22. 如图,点 A,B,C均在6×6的正方形网格格点上,过A,B,C三点的外接圆除经过A,B,C三点外还能经过的格点数为.
 23. 如图,AB是半圆O的直径,半圆的半径为4,点C,D在半圆上, , 点P是OC上的一个动点,则的最小值为 .
23. 如图,AB是半圆O的直径,半圆的半径为4,点C,D在半圆上, , 点P是OC上的一个动点,则的最小值为 .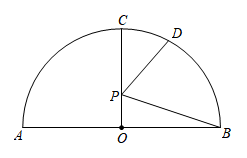 24. 如图,在中,AD为直径,弦于点H,连接OB.已知 , . 动点E从点O出发,在直径AD上沿路线以1cm/s的速度做匀速往返运动,运动时间为 . 当时,的值为 .
24. 如图,在中,AD为直径,弦于点H,连接OB.已知 , . 动点E从点O出发,在直径AD上沿路线以1cm/s的速度做匀速往返运动,运动时间为 . 当时,的值为 .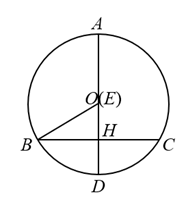 25. 如图,大圆和小圆是等边三角形的外接圆和内切圆,现随机向该图形内掷一枚小针,则针尖落在小圆区域的概率为 .
25. 如图,大圆和小圆是等边三角形的外接圆和内切圆,现随机向该图形内掷一枚小针,则针尖落在小圆区域的概率为 .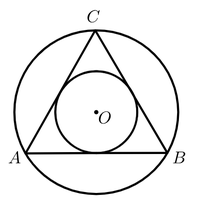 26. 如图,在平面直角坐标系中,点A,B,C的横、纵坐标都为整数,过这三个点作一条圆弧,则此圆弧的圆心坐标为 .
26. 如图,在平面直角坐标系中,点A,B,C的横、纵坐标都为整数,过这三个点作一条圆弧,则此圆弧的圆心坐标为 . 27. 如图,和都是等边三角形, , , 固定 , 把绕点C旋转任意角度,连接AD,BE,设AD,BE所在的直线交于点O,则在旋转过程中,始终有 , 且的大小保持不变,这时点O到直线AB的最大距离为 .
27. 如图,和都是等边三角形, , , 固定 , 把绕点C旋转任意角度,连接AD,BE,设AD,BE所在的直线交于点O,则在旋转过程中,始终有 , 且的大小保持不变,这时点O到直线AB的最大距离为 .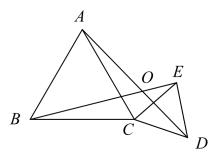 28. 如图,在Rt△ABC中,∠C=90°,AC=9,BC=4,以点C为圆心,3为半径做⊙C,分别交AC,BC于D,E两点,点P是⊙C上一个动点,则PA+PB的最小值为 .
28. 如图,在Rt△ABC中,∠C=90°,AC=9,BC=4,以点C为圆心,3为半径做⊙C,分别交AC,BC于D,E两点,点P是⊙C上一个动点,则PA+PB的最小值为 .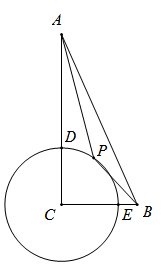 29. 如图,△ABC为⊙O的内接等边三角形,BC=12,点D为 上一动点,BE⊥OD于E,当点D由点B沿 运动到点C时,线段AE的最大值是 .
29. 如图,△ABC为⊙O的内接等边三角形,BC=12,点D为 上一动点,BE⊥OD于E,当点D由点B沿 运动到点C时,线段AE的最大值是 . 30. 图1是邻边长为2和6的矩形,它由三个小正方形组成,将其剪拼成不重叠、无缝隙的大正方形(如图2),则图1中所标注的 的值为;记图1中小正方形的中心为点 , , ,图2中的对应点为点 , , .以大正方形的中心 为圆心作圆,则当点 , , 在圆内或圆上时,圆的最小面积为.
30. 图1是邻边长为2和6的矩形,它由三个小正方形组成,将其剪拼成不重叠、无缝隙的大正方形(如图2),则图1中所标注的 的值为;记图1中小正方形的中心为点 , , ,图2中的对应点为点 , , .以大正方形的中心 为圆心作圆,则当点 , , 在圆内或圆上时,圆的最小面积为.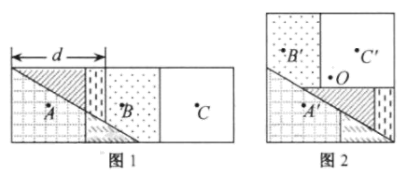
三、解答题
-
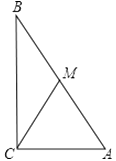
31. 已知⊙O的半径为2,点P到圆心O的距离OP=m,且m使关于x的方程 有实数根,求点P与⊙O的位置关系.32. 已知:如图,△ABC中, , cm, cm,CM是中线,以C为圆心,以 cm长为半径画圆,则点A、B、M与⊙C的关系如何?
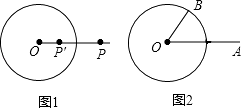
 33. 如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′•OP=r2 , 则称点P′是点P关于⊙O的“反演点”.
33. 如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′•OP=r2 , 则称点P′是点P关于⊙O的“反演点”.如图2,⊙O的半径为4,点B在⊙O上,∠BOA=60°,OA=8,若点A′,B′分别是点A,B关于⊙O的反演点,求A′B′的长.
 34. 如图,在Rt△ABC中,∠ABC=90°,点F为AC中点,⊙O经过点B,F,且与AC交于点D,与AB交于点E,与BC交于点G,连结BF,DE,弧EFG的长度为(1+)π.
34. 如图,在Rt△ABC中,∠ABC=90°,点F为AC中点,⊙O经过点B,F,且与AC交于点D,与AB交于点E,与BC交于点G,连结BF,DE,弧EFG的长度为(1+)π.(1)求⊙O的半径;
(2)若DE∥BF,且AE=a,DF=2+﹣a,请判断圆心O和直线BF的位置关系,并说明理由.
 35. 如图,在直角坐标系中,直线 与 轴交于 点,与 轴交于 点,以 为直径作圆 ,过 作圆 的切线交 轴于点 .
35. 如图,在直角坐标系中,直线 与 轴交于 点,与 轴交于 点,以 为直径作圆 ,过 作圆 的切线交 轴于点 . (1)、求 点的坐标;(2)、设点 为 延长线上一点, , 为线段 上的一个动点(异于 , ),过 点作 轴的平行线交 于 ,交 的延长线于 ,试判断 的值是否为定值,如果是,则求出这个值;如果不是,请说明理由.36. 对于平面内的⊙C和⊙C外一点Q,给出如下定义:若过点Q的直线与⊙C存在公共点,记为点A,B,设 ,则称点A(或点B)是⊙C的“K相关依附点”,特别地,当点A和点B重合时,规定AQ=BQ, (或 ).
(1)、求 点的坐标;(2)、设点 为 延长线上一点, , 为线段 上的一个动点(异于 , ),过 点作 轴的平行线交 于 ,交 的延长线于 ,试判断 的值是否为定值,如果是,则求出这个值;如果不是,请说明理由.36. 对于平面内的⊙C和⊙C外一点Q,给出如下定义:若过点Q的直线与⊙C存在公共点,记为点A,B,设 ,则称点A(或点B)是⊙C的“K相关依附点”,特别地,当点A和点B重合时,规定AQ=BQ, (或 ).已知在平面直角坐标系xOy中,Q(-1,0),C(1,0),⊙C的半径为r.
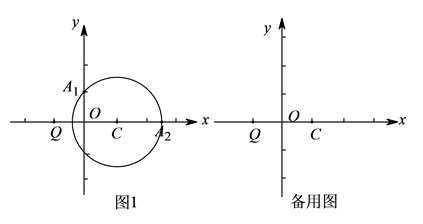 (1)、如图1,当 时,
(1)、如图1,当 时,①若A1(0,1)是⊙C的“k相关依附点”,求k的值.
②A2(1+ ,0)是否为⊙C的“2相关依附点”.
(2)、若⊙C上存在“k相关依附点”点M,①当r=1,直线QM与⊙C相切时,求k的值.
②当 时,求r的取值范围.
(3)、若存在r的值使得直线 与⊙C有公共点,且公共点时⊙C的“ 相关依附点”,直接写出b的取值范围.四、综合题
-
37. 如图①,在矩形ABCD中,BC=60cm.动点P以6cm/s的速度在矩形ABCD的边上沿A→D的方向匀速运动,动点Q在矩形ABCD的边上沿A→B→C的方向匀速运动.P、Q两点同时出发,当点P到达终点D时,点Q立即停止运动.设运动的时间为t(s),△PDQ的面积为S(cm2),S与t的函数图象如图②所示.
 (1)、AB=cm,点Q的运动速度为cm/s;(2)、在点P、Q出发的同时,点O也从CD的中点出发,以4cm/s的速度沿CD的垂直平分线向左匀速运动,以点O为圆心的⊙O始终与边AD、BC相切,当点P到达终点D时,运动同时停止.
(1)、AB=cm,点Q的运动速度为cm/s;(2)、在点P、Q出发的同时,点O也从CD的中点出发,以4cm/s的速度沿CD的垂直平分线向左匀速运动,以点O为圆心的⊙O始终与边AD、BC相切,当点P到达终点D时,运动同时停止.①当点O在QD上时,求t的值;
②当PQ与⊙O有公共点时,求t的取值范围.
38. 如图,四边形ABCD是⊙O 的内接四边形,对角线AC,BD交于点E,AB=AC. (1)、如图1,若BD是⊙O的直径,求证:∠BAC=2∠ACD;(2)、如图2,若BD⊥AC,DE =3,CE=4,求BE的长;(3)、如图3,若∠ABC+∠DCB=90°,AD=7,BC=24,求AB的长;(4)、在(3)的条件下,保持BC不动,使AD在⊙O上滑动,(滑动中AD长度保持不变)直接写出BD+AC的最大值.
(1)、如图1,若BD是⊙O的直径,求证:∠BAC=2∠ACD;(2)、如图2,若BD⊥AC,DE =3,CE=4,求BE的长;(3)、如图3,若∠ABC+∠DCB=90°,AD=7,BC=24,求AB的长;(4)、在(3)的条件下,保持BC不动,使AD在⊙O上滑动,(滑动中AD长度保持不变)直接写出BD+AC的最大值.