2022年初中数学苏科版《中考二轮复习》专题二 函数 2.2 反比例函数
试卷更新日期:2022-04-15 类型:二轮复习
一、单选题
-
1. 已知反比例函数 与一次函数叫 的图象没有交点,则k的值可以是( )A、 B、 C、 D、-12. 如图,函数y=kx+b(k≠0)与y= (m≠0)的图象交于点A(2,3),B(-6,-1),则不等式kx+b> 的解集为( )
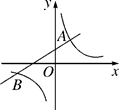 A、x<-6或0<x<2 B、-6<x或x>2 C、 D、3. 一次函数 的图象与x轴交于点B,与反比例函数 的图象交于点 ,且 的面积为1,则m的值是( )A、1 B、2 C、3 D、44. 下列选项中,阴影部分面积最小的是( )A、
A、x<-6或0<x<2 B、-6<x或x>2 C、 D、3. 一次函数 的图象与x轴交于点B,与反比例函数 的图象交于点 ,且 的面积为1,则m的值是( )A、1 B、2 C、3 D、44. 下列选项中,阴影部分面积最小的是( )A、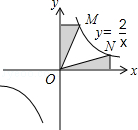 B、
B、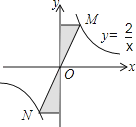 C、
C、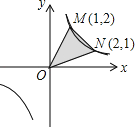 D、
D、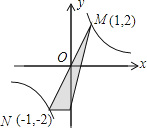 5. 平面直角坐标系 中,直线 与双曲线 相交于A,B两点,其中点A在第一象限.设 为双曲线 上一点,直线 , 分别交y轴于C,D两点,则 的值为( )A、2 B、4 C、6 D、86. 已知点A是双曲线y= 在第一象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y= (x>0)上运动,则k的值是( )
5. 平面直角坐标系 中,直线 与双曲线 相交于A,B两点,其中点A在第一象限.设 为双曲线 上一点,直线 , 分别交y轴于C,D两点,则 的值为( )A、2 B、4 C、6 D、86. 已知点A是双曲线y= 在第一象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y= (x>0)上运动,则k的值是( )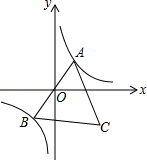 A、3 B、 C、﹣3 D、﹣7.
A、3 B、 C、﹣3 D、﹣7.如图,已知△ABO的顶点A和AB边的中点C都在双曲线y=(x>0)的一个分支上,点B在x轴上,CD⊥OB于D,若△AOC的面积为3,则k的值为( )
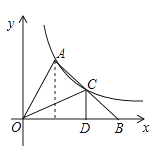 A、2 B、3 C、4 D、8. 如图,点 在反比例函数 ( )的图象上,点 在反比例函数 ( )的图象上,且 轴, ,垂足为点 ,交 轴于点 .则 的面积为( )
A、2 B、3 C、4 D、8. 如图,点 在反比例函数 ( )的图象上,点 在反比例函数 ( )的图象上,且 轴, ,垂足为点 ,交 轴于点 .则 的面积为( ) A、3 B、4 C、5 D、69. 在平面直角坐标系中,平行四边形ABCD的顶点A在y轴上,点C坐标为(﹣4,0),E为BC上靠近点C的三等分点,点B、E均在反比例函数y= (k<0,x<0)的图象上,若tan∠OAD= ,则k的值为( )
A、3 B、4 C、5 D、69. 在平面直角坐标系中,平行四边形ABCD的顶点A在y轴上,点C坐标为(﹣4,0),E为BC上靠近点C的三等分点,点B、E均在反比例函数y= (k<0,x<0)的图象上,若tan∠OAD= ,则k的值为( )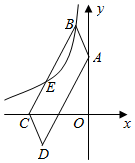 A、﹣2 B、﹣2 C、﹣6 D、﹣410. 如图,点P是函数 的图像上一点,过点P分别作x轴和y轴的垂线,垂足分别为点A、B,交函数 的图像于点C、D,连接 、 、 、 ,其中 ,下列结论:① ;② ;③ ,其中正确的是( )
A、﹣2 B、﹣2 C、﹣6 D、﹣410. 如图,点P是函数 的图像上一点,过点P分别作x轴和y轴的垂线,垂足分别为点A、B,交函数 的图像于点C、D,连接 、 、 、 ,其中 ,下列结论:① ;② ;③ ,其中正确的是( )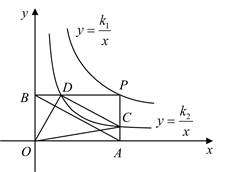 A、①② B、①③ C、②③ D、①
A、①② B、①③ C、②③ D、①二、填空题
-
11. 设直线y=kx(k<0)与双曲线y=﹣ 相交于A(x1 , y1)、B(x2 , y2)两点,则x1y2﹣3x2y1的值为.12. 如图,△ABC的顶点A在反比例函数y= (x>0)的图象上,顶点C在x轴上,AB∥x轴,若点B的坐标为(1,3),S△ABC=2,则k的值.
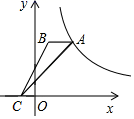 13. 如图,点E、F在反比例函数y= (x>0)的图象上,直线EF分别与x、y轴交于点A、B,且BE:BF=1:3,则S△OEF=.
13. 如图,点E、F在反比例函数y= (x>0)的图象上,直线EF分别与x、y轴交于点A、B,且BE:BF=1:3,则S△OEF=.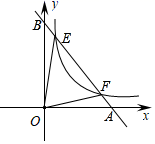 14. 如图,点A在双曲线 上,点B在双曲线 上,且 轴,C、D在x轴上,若四边形ABCD为平行四边形,则它的面积为.
14. 如图,点A在双曲线 上,点B在双曲线 上,且 轴,C、D在x轴上,若四边形ABCD为平行四边形,则它的面积为.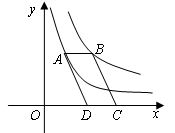 15. 如图,菱形 顶点 在函数 的图象上,函数 的图象关于直线 对称,且经过点 , 两点,若 , ,则 的值为.
15. 如图,菱形 顶点 在函数 的图象上,函数 的图象关于直线 对称,且经过点 , 两点,若 , ,则 的值为.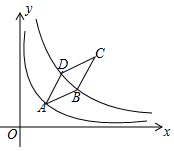 16. 如图,菱形 中, ,顶点 在双曲线 上,顶点 在双曲线 上,且 经过点O.若 ,则菱形 面积的最小值是.
16. 如图,菱形 中, ,顶点 在双曲线 上,顶点 在双曲线 上,且 经过点O.若 ,则菱形 面积的最小值是.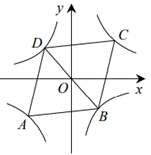 17. 如图所示,点A1、A2、A3在x轴上,且OA1=A1A2=A2A3 , 分别过点A1、A2、A3作y轴的平行线,与反比例函数y= (x>0)的图象分别交于点B1、B2、B3 , 分别过点B1、B2、B3作x轴的平行线,分别与y轴交于点C1、C2、C3 , 连接OB1、OB2、OB3 , 若图中三个阴影部分的面积之和为 ,则k=.
17. 如图所示,点A1、A2、A3在x轴上,且OA1=A1A2=A2A3 , 分别过点A1、A2、A3作y轴的平行线,与反比例函数y= (x>0)的图象分别交于点B1、B2、B3 , 分别过点B1、B2、B3作x轴的平行线,分别与y轴交于点C1、C2、C3 , 连接OB1、OB2、OB3 , 若图中三个阴影部分的面积之和为 ,则k=.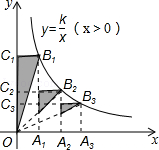 18. 如图,一次函数 = 与反比例函数 = ( >0)的图象交于A,B两点,点P在以C(-2,0)为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最小值为 ,则 的值为.
18. 如图,一次函数 = 与反比例函数 = ( >0)的图象交于A,B两点,点P在以C(-2,0)为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最小值为 ,则 的值为.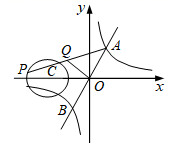
三、综合题
-
19. 设反比例函数的解析式为y= (k>0).
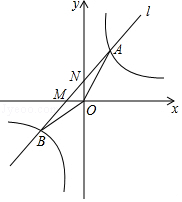 (1)、若该反比例函数与正比例函数y=2x的图象有一个交点的纵坐标为2,求k的值;(2)、若该反比例函数与过点M(﹣2,0)的直线l:y=kx+b的图象交于A,B两点,如图所示,当△ABO的面积为 时,求直线l的解析式.20. 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数 的图象交于二四象限内的A、B 两点,与x轴交于C点,点B的坐标为(6,n),线段OA=5,E为x轴负半轴上一点,且sin∠AOE= .
(1)、若该反比例函数与正比例函数y=2x的图象有一个交点的纵坐标为2,求k的值;(2)、若该反比例函数与过点M(﹣2,0)的直线l:y=kx+b的图象交于A,B两点,如图所示,当△ABO的面积为 时,求直线l的解析式.20. 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数 的图象交于二四象限内的A、B 两点,与x轴交于C点,点B的坐标为(6,n),线段OA=5,E为x轴负半轴上一点,且sin∠AOE= .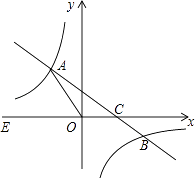 (1)、求该反比例函数和一次函数的解析式;(2)、求△AOC的面积;(3)、直接写出一次函数值大于反比例函数值时自变量x的取值范围.21. 如图所示,直线y=x+b与双曲线y= (x<0)交于点A(﹣1,﹣5),并分别与x轴、y轴交于点C、B.
(1)、求该反比例函数和一次函数的解析式;(2)、求△AOC的面积;(3)、直接写出一次函数值大于反比例函数值时自变量x的取值范围.21. 如图所示,直线y=x+b与双曲线y= (x<0)交于点A(﹣1,﹣5),并分别与x轴、y轴交于点C、B.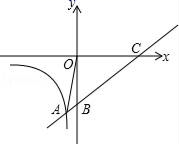 (1)、求出b、m的值;(2)、点D在x轴的正半轴上,若以点D、C、B组成的三角形与△OAB相似,试求点D的坐标.22. 如图,一次函数y=kx+b与反比例函数y= 的图象交于A(1,4)、B(﹣4,n)两点.
(1)、求出b、m的值;(2)、点D在x轴的正半轴上,若以点D、C、B组成的三角形与△OAB相似,试求点D的坐标.22. 如图,一次函数y=kx+b与反比例函数y= 的图象交于A(1,4)、B(﹣4,n)两点.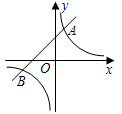 (1)、求反比例函数和一次函数的解析式;(2)、在图中连接OA、OB,求△AOB的面积;(3)、点P是x轴上的一动点,试确定点P并求出它的坐标,使∠APB是直角.23. 如图,一次函数 的图象与反比例函数 的图象相交于A、B两点,点C在x轴负半轴上,点 ,连接OA、OD、DC、AC,四边形 为菱形.
(1)、求反比例函数和一次函数的解析式;(2)、在图中连接OA、OB,求△AOB的面积;(3)、点P是x轴上的一动点,试确定点P并求出它的坐标,使∠APB是直角.23. 如图,一次函数 的图象与反比例函数 的图象相交于A、B两点,点C在x轴负半轴上,点 ,连接OA、OD、DC、AC,四边形 为菱形.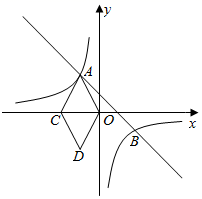 (1)、求一次函数与反比例函数的解析式;(2)、根据图象,直接写出反比例函数的值小于2时,x的取值范围;(3)、设点P是直线AB上一动点,且 ,求点P的坐标.24. “净扬”水净化有限公司用160万元,作为新产品的研发费用,成功研制出了一种市场急需的小型水净化产品,已于当年投入生产并进行销售.已知生产这种小型水净化产品的成本为4元/件,在销售过程中发现:每年的年销售量 (万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种水净化产品的年利润为z(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)
(1)、求一次函数与反比例函数的解析式;(2)、根据图象,直接写出反比例函数的值小于2时,x的取值范围;(3)、设点P是直线AB上一动点,且 ,求点P的坐标.24. “净扬”水净化有限公司用160万元,作为新产品的研发费用,成功研制出了一种市场急需的小型水净化产品,已于当年投入生产并进行销售.已知生产这种小型水净化产品的成本为4元/件,在销售过程中发现:每年的年销售量 (万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种水净化产品的年利润为z(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)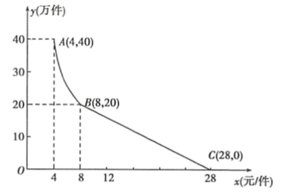 (1)、请求出y(万件)与x(元/件)之间的函数关系式;(2)、求出第一年这种水净化产品的年利润z(万元)与x(元/件)之间的函数关系式,并求出第一年年利润的最大值;(3)、假设公司的这种水净化产品第一年恰好按年利润z(万元)取得最大值时进行销售,现根据第一年的盈亏情况,决定第二年将这种水净化产品每件的销售价格x(元)定在8元以上( ),当第二年的年利润不低于103万元时,请结合年利润z(万元)与销售价格x(元/件)的函数示意图,求销售价格x(元/件)的取值范围.25. 如图①,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形. .反比例函数 在第一象限内的图象经过点A,交BC的中点F.且 .
(1)、请求出y(万件)与x(元/件)之间的函数关系式;(2)、求出第一年这种水净化产品的年利润z(万元)与x(元/件)之间的函数关系式,并求出第一年年利润的最大值;(3)、假设公司的这种水净化产品第一年恰好按年利润z(万元)取得最大值时进行销售,现根据第一年的盈亏情况,决定第二年将这种水净化产品每件的销售价格x(元)定在8元以上( ),当第二年的年利润不低于103万元时,请结合年利润z(万元)与销售价格x(元/件)的函数示意图,求销售价格x(元/件)的取值范围.25. 如图①,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形. .反比例函数 在第一象限内的图象经过点A,交BC的中点F.且 .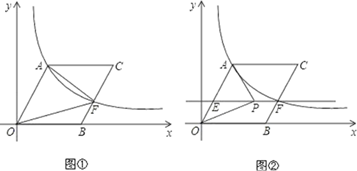 (1)、求k值和点C的坐标;(2)、过点F作EF∥OB,交OA于点E(如图②),点P为直线EF上的一个动点,连接PA,PO.是否存在这样的点P,使以P、O、A为顶点的三角形是直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.26. 有一边是另一边的 倍的三角形叫做智慧三角形,这两边中较长边称为智慧边,这两边的 夹角叫做智慧角.
(1)、求k值和点C的坐标;(2)、过点F作EF∥OB,交OA于点E(如图②),点P为直线EF上的一个动点,连接PA,PO.是否存在这样的点P,使以P、O、A为顶点的三角形是直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.26. 有一边是另一边的 倍的三角形叫做智慧三角形,这两边中较长边称为智慧边,这两边的 夹角叫做智慧角.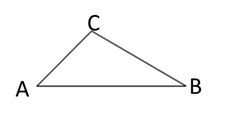
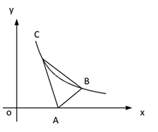 (1)、在 Rt△ABC 中,∠ACB=90°,若∠A 为智慧角,则∠B 的度数为;(2)、如图①,在△ABC 中,∠A=45°,∠B=30°,求证:△ABC 是智慧三角形;(3)、如图②,△ABC 是智慧三角形,BC 为智慧边,∠B 为智慧角,A(3,0),点 B,C 在函数 y= (x>0)的图象上,点 C 在点 B 的上方,且点 B 的纵坐标为 .当△ABC是直角三角形时,求k的值.27. 如图,在平面直角坐标系中,直线y=kx﹣4与反比例函数y= (x>0)的图象交于点A,与y轴交于点C.点B在x轴上,∠ABO=90°,AB=BO.
(1)、在 Rt△ABC 中,∠ACB=90°,若∠A 为智慧角,则∠B 的度数为;(2)、如图①,在△ABC 中,∠A=45°,∠B=30°,求证:△ABC 是智慧三角形;(3)、如图②,△ABC 是智慧三角形,BC 为智慧边,∠B 为智慧角,A(3,0),点 B,C 在函数 y= (x>0)的图象上,点 C 在点 B 的上方,且点 B 的纵坐标为 .当△ABC是直角三角形时,求k的值.27. 如图,在平面直角坐标系中,直线y=kx﹣4与反比例函数y= (x>0)的图象交于点A,与y轴交于点C.点B在x轴上,∠ABO=90°,AB=BO.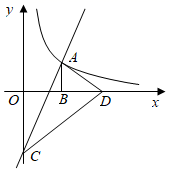 (1)、求k的值;(2)、点D(m,0)在x轴正半轴上,连接AD,CD, ACD是以AC为斜边的直角三角形.请用两种不同的方法求m的值.(3)、在(2)的条件下,点E在反比例函数的图象上(不与A重合),若 ,请求出点E的坐标.(4)、若P为直线y=kx﹣4上的动点,Q为反比例函数y= (x>0)的图象上的动点,且以点P、Q、O、C为顶点的四边形是平行四边形,请直接写出点P的坐标.28. 如图
(1)、求k的值;(2)、点D(m,0)在x轴正半轴上,连接AD,CD, ACD是以AC为斜边的直角三角形.请用两种不同的方法求m的值.(3)、在(2)的条件下,点E在反比例函数的图象上(不与A重合),若 ,请求出点E的坐标.(4)、若P为直线y=kx﹣4上的动点,Q为反比例函数y= (x>0)的图象上的动点,且以点P、Q、O、C为顶点的四边形是平行四边形,请直接写出点P的坐标.28. 如图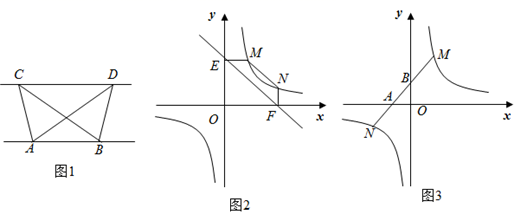 (1)、(探究新知)如图1,已知 与 的面积相等,试判断 与 的位置关系,并说明理由.(2)、(结论应用)如图2,点M,N在反比例函数 的图象上,过点M作 轴,过点N作 轴,垂足分别为E,F.试证明: .(3)、(拓展延伸)若第(2)问中的其他条件不变,只改变点M,N在反比例函数 图象上的位置,如图3所示, 与x轴、y轴分别交于点A、点B,若 ,请求 的长.
(1)、(探究新知)如图1,已知 与 的面积相等,试判断 与 的位置关系,并说明理由.(2)、(结论应用)如图2,点M,N在反比例函数 的图象上,过点M作 轴,过点N作 轴,垂足分别为E,F.试证明: .(3)、(拓展延伸)若第(2)问中的其他条件不变,只改变点M,N在反比例函数 图象上的位置,如图3所示, 与x轴、y轴分别交于点A、点B,若 ,请求 的长.