2022年初中数学苏科版《中考二轮复习》专题二 函数 2.1 一次函数
试卷更新日期:2022-04-15 类型:二轮复习
一、单选题
-
1. 函数y= x﹣3的图象与x轴、y轴分别交于A、B两点,点C在x轴上.若△ABC为等腰三角形,则满足条件的点C共有( )A、4个 B、3个 C、2个 D、1个2. 已知点 在经过原点的一条直线l上,且 ,则 的值为( )A、 B、 C、0 D、-13. 如图,在平面直角坐标系中,点A的坐标为 , 沿x轴向右平移后得到A',A点的对应点A'在直线上,则点B与其对应点B'之间的距离为( )
 A、4 B、6 C、8 D、104. 如图,四边形 的顶点坐标分别为 ,当过点 的直线 将四边形 分成面积相等的两部分时,直线 所表示的函数表达式为( )
A、4 B、6 C、8 D、104. 如图,四边形 的顶点坐标分别为 ,当过点 的直线 将四边形 分成面积相等的两部分时,直线 所表示的函数表达式为( )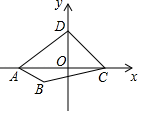 A、 B、 C、 D、5. 如图,直线 与 轴、 轴分别相交于点A、B,过点B作 ,使 .将 绕点 顺时针旋转,每次旋转 .则第2022次旋转结束时,点 的对应点 落在反比例函数 的图象上,则 的值为
A、 B、 C、 D、5. 如图,直线 与 轴、 轴分别相交于点A、B,过点B作 ,使 .将 绕点 顺时针旋转,每次旋转 .则第2022次旋转结束时,点 的对应点 落在反比例函数 的图象上,则 的值为 A、-4 B、4 C、-6 D、66. 甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶 ,并且甲车途中休息了 ,如图是甲、乙两车行驶的距离 与时间 的函数图象,有以下结论:
A、-4 B、4 C、-6 D、66. 甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶 ,并且甲车途中休息了 ,如图是甲、乙两车行驶的距离 与时间 的函数图象,有以下结论:① ;② ;③甲车从A地到B地共用了7小时;④当两车相距 时,乙车用时为 .其中正确结论的个数是( ).
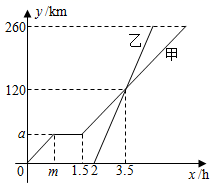 A、4 B、3 C、2 D、17. 如图,在平面直角坐标系中,点A在一次函数y= x位于第一象限的图象上运动,点B在x轴正半轴上运动,在AB右侧以它为边作矩形ABCD,且AB=2 ,AD=1,则OD的最大值是( )
A、4 B、3 C、2 D、17. 如图,在平面直角坐标系中,点A在一次函数y= x位于第一象限的图象上运动,点B在x轴正半轴上运动,在AB右侧以它为边作矩形ABCD,且AB=2 ,AD=1,则OD的最大值是( )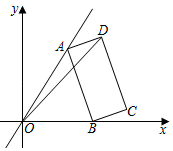 A、 B、 +2 C、 +2 D、8. 如图,直线y=kx+b(k、b为常数)分别与x轴、y轴交于点A(﹣4,0)、B(0,3),抛物线y=﹣x2+2x+1与y轴交于点C,点E在抛物线y=﹣x2+2x+1的对称轴上移动,点F在直线AB上移动,CE+EF的最小值是( )
A、 B、 +2 C、 +2 D、8. 如图,直线y=kx+b(k、b为常数)分别与x轴、y轴交于点A(﹣4,0)、B(0,3),抛物线y=﹣x2+2x+1与y轴交于点C,点E在抛物线y=﹣x2+2x+1的对称轴上移动,点F在直线AB上移动,CE+EF的最小值是( ) A、1.4 B、2.5 C、2.8 D、39. 如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0)直线y=kx-3k+4与 交于B、C两点,则弦BC的长的最小值为( )
A、1.4 B、2.5 C、2.8 D、39. 如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0)直线y=kx-3k+4与 交于B、C两点,则弦BC的长的最小值为( ) A、22 B、24 C、 D、10. 如图,在平面直角坐标系xOy中,半径为2的⊙O与x轴的正半轴交于点A,点B是⊙O上一动点,点C为弦AB的中点,直线y= x﹣3与x轴、y轴分别交于点D、E,则△CDE面积的最小值为( )
A、22 B、24 C、 D、10. 如图,在平面直角坐标系xOy中,半径为2的⊙O与x轴的正半轴交于点A,点B是⊙O上一动点,点C为弦AB的中点,直线y= x﹣3与x轴、y轴分别交于点D、E,则△CDE面积的最小值为( ) A、3.5 B、2.5 C、2 D、1.2
A、3.5 B、2.5 C、2 D、1.2二、填空题
-
11. 在平面直角坐标系中,若将一次函数y=2x+m-1的图象向右平移3个单位后,得到一个正比例函数的图象,则m的值为 .12. 平面直角坐标系 中,已知点 在直线 上,且满足 ,则 .13. 在平面直角坐标系中,已知点 ,点 ,点P在一次函数 的图象上,若满足 的点P只有1个,则b的取值范围是.14. 如图,已知直线 与 轴、 轴分别交于 、 两点, 是以 为圆心、半径为1的圆上的一动点,连接 、 .则 面积的最大值是.
 15. 如图,在平面直角坐标系中,点P的坐标为(- m,m)(m>0),过点P的直线AB与x轴负半轴交于点A,与直线y=- x交于点B.若点A的坐标是(-6,0),且2AP=3PB,则直线AB的函数表达式为.
15. 如图,在平面直角坐标系中,点P的坐标为(- m,m)(m>0),过点P的直线AB与x轴负半轴交于点A,与直线y=- x交于点B.若点A的坐标是(-6,0),且2AP=3PB,则直线AB的函数表达式为. 16. 如图,在平面直角坐标系中,直线l: 与坐标轴分别交于A,B两点,点C在x正半轴上,且OC=OB.点P为线段AB(不含端点)上一动点,将线段OP绕点O顺时针旋转90°得线段OQ,连接CQ,则线段CQ的最小值为.
16. 如图,在平面直角坐标系中,直线l: 与坐标轴分别交于A,B两点,点C在x正半轴上,且OC=OB.点P为线段AB(不含端点)上一动点,将线段OP绕点O顺时针旋转90°得线段OQ,连接CQ,则线段CQ的最小值为. 17. 如图,已知点A是第一象限内横坐标为 的一个定点,AC⊥x轴于点M,交直线y=-x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是.
17. 如图,已知点A是第一象限内横坐标为 的一个定点,AC⊥x轴于点M,交直线y=-x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是.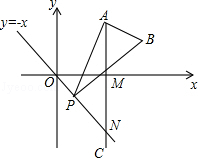 18. 如图,在平面直角坐标系中,直线 为正比例函数 的图象,点 的坐标为(1,0),过点 作 轴的垂线交直线 于点 ,以 为边作正方形 ;过点 作直线 的垂线,垂足为 ,交 轴于点 ,以 为边作正方形 ;过点 作 轴的垂线,垂足为 ,交直线 于点 ,以 为边作正方形 ,…,按此规律操作下所得到的正方形 的面积是.
18. 如图,在平面直角坐标系中,直线 为正比例函数 的图象,点 的坐标为(1,0),过点 作 轴的垂线交直线 于点 ,以 为边作正方形 ;过点 作直线 的垂线,垂足为 ,交 轴于点 ,以 为边作正方形 ;过点 作 轴的垂线,垂足为 ,交直线 于点 ,以 为边作正方形 ,…,按此规律操作下所得到的正方形 的面积是.
三、综合题
-
19. 如图,一次函数 的图象与反比例函数 的图象相交于A、B两点,且与x轴交于点 C,点A的坐标为(2,3),点B的坐标为(-6,n).
 (1)、求一次函数与反比例函数的解析式;(2)、连接AO、OB,求△AOB的面积;(3)、结合图象直接写出不等式组 的解集.20. “夕阳红”养老院共有普通床位和高档床位共500张.已知今年一月份入住普通床位老人300人,入住高档床位老人90人,共计收费51万元;今年二月份入住普通床位老人350人,入住高档床位老人100人,共计收费58万元.(1)、求普通床位和高档床位每月收费各多少元?(2)、根据国家养老政策规定,为保障普通居民的养老权益,所有实际入住高档床位数不得超过实际入住普通床位数的三分之一;另外为扶持养老企业发展国家民政局财政对每张入住的床位平均每年都是给予养老院企业2400元的补贴.经测算,该养老院普通床位的运营成本是每月1200元/张,入住率为90%;高档床位的运营成本是每月2000元/张,入住率为70%.问该养老院应该怎样安排500张床的普通床位和高档床位数量,才能使每月的利润最大,最大为多少元?(月利润=月收费-月成本+月补贴)21. 某地实施产业扶贫种植某种水果,其成本经过测算为20元 , 投放市场后,经过市场调研发现,这种水果在上市的一段时间内的销售单价p(元)与时间t(天)之间的函数图象如图,且其日销售量y()与时间t(天)的关系是: , 天数为整数.
(1)、求一次函数与反比例函数的解析式;(2)、连接AO、OB,求△AOB的面积;(3)、结合图象直接写出不等式组 的解集.20. “夕阳红”养老院共有普通床位和高档床位共500张.已知今年一月份入住普通床位老人300人,入住高档床位老人90人,共计收费51万元;今年二月份入住普通床位老人350人,入住高档床位老人100人,共计收费58万元.(1)、求普通床位和高档床位每月收费各多少元?(2)、根据国家养老政策规定,为保障普通居民的养老权益,所有实际入住高档床位数不得超过实际入住普通床位数的三分之一;另外为扶持养老企业发展国家民政局财政对每张入住的床位平均每年都是给予养老院企业2400元的补贴.经测算,该养老院普通床位的运营成本是每月1200元/张,入住率为90%;高档床位的运营成本是每月2000元/张,入住率为70%.问该养老院应该怎样安排500张床的普通床位和高档床位数量,才能使每月的利润最大,最大为多少元?(月利润=月收费-月成本+月补贴)21. 某地实施产业扶贫种植某种水果,其成本经过测算为20元 , 投放市场后,经过市场调研发现,这种水果在上市的一段时间内的销售单价p(元)与时间t(天)之间的函数图象如图,且其日销售量y()与时间t(天)的关系是: , 天数为整数. (1)、试求销售单价p(元)与时间t(天)之间的函数关系式;(2)、哪一天的销售利润最大?最大日销售利润为多少?(3)、在实际销售的前28天中,公司决定每销售水果就捐赠n元利润()给“精准扶贫”对象.现发现:在前28天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.22. 东坡商贸公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为 ,且其日销售量y(kg)与时间t(天)的关系如表:
(1)、试求销售单价p(元)与时间t(天)之间的函数关系式;(2)、哪一天的销售利润最大?最大日销售利润为多少?(3)、在实际销售的前28天中,公司决定每销售水果就捐赠n元利润()给“精准扶贫”对象.现发现:在前28天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.22. 东坡商贸公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为 ,且其日销售量y(kg)与时间t(天)的关系如表:时间t(天)
1
3
6
10
20
40
…
日销售量y(kg)
118
114
108
100
80
40
…
(1)、已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?(2)、问哪一天的销售利润最大?最大日销售利润为多少?(3)、在实际销售的前24天中,公司决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.23. 上午8点,某台风中心在A岛正南方向 处由南向北匀速移动,同时在A岛正西方向 处有一艘补给船向A岛匀速驶来,补给完后改变速度立即向A岛正北方向的C港匀速驶去,如图所示是台风中心、补给船与A岛的距离S和时间t的图象.已知台风影响的半径是 (包含边界),请结合图象解答下列问题: (1)、台风的速度是 ,补给船在到达A岛前的速度是 ,图中点P的实际意义是;(2)、从几点开始,补给船将受到台风的影响?(3)、设补给船驶出A岛到驶到C港之前受到台风影响的时间为a小时,出于安全考虑,补给船速度不超过 、 .求出图中补给船航行时间m的正整数值及此时补给船在驶入C港之前受台风影响的总时间.24. 如图(1),四边形ABCD的顶点A、D、C分别在x、y轴的正半轴上,AD∥BC,OC=4cm.动点E从点C出发,沿C→D→A→B→C匀速运动,动点F以每秒1cm的速度从C出发沿线段CB向点B来回运动,当E点运动到点C点时,两点同时停止运动.若点E、F同时出发运动t秒后,如图(2)是△OEC的面积S(cm2)与t(秒)的函数关系图象,以线段EF为斜边向右作等腰直角△EFG.
(1)、台风的速度是 ,补给船在到达A岛前的速度是 ,图中点P的实际意义是;(2)、从几点开始,补给船将受到台风的影响?(3)、设补给船驶出A岛到驶到C港之前受到台风影响的时间为a小时,出于安全考虑,补给船速度不超过 、 .求出图中补给船航行时间m的正整数值及此时补给船在驶入C港之前受台风影响的总时间.24. 如图(1),四边形ABCD的顶点A、D、C分别在x、y轴的正半轴上,AD∥BC,OC=4cm.动点E从点C出发,沿C→D→A→B→C匀速运动,动点F以每秒1cm的速度从C出发沿线段CB向点B来回运动,当E点运动到点C点时,两点同时停止运动.若点E、F同时出发运动t秒后,如图(2)是△OEC的面积S(cm2)与t(秒)的函数关系图象,以线段EF为斜边向右作等腰直角△EFG.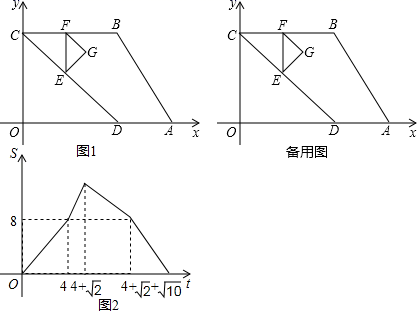 (1)、填空:点E的运动速度是 , B点坐标为.(2)、当0≤t<4秒时,
(1)、填空:点E的运动速度是 , B点坐标为.(2)、当0≤t<4秒时,①t为何值时,以O、C、E为顶点的三角形与△BFG相似?
②是否存在这样的时刻t,使点G正好落在线段AB上,若存在,求此时的t,若不存在,请说明理由.
25. 对于⊙C与⊙C上一点A,若平面内的点P满足:射线AP与⊙C交于点Q,且PA=2QA,则称点P为点A关于⊙C的“倍距点”.已知平面直角坐标系xOy中,点A的坐标是(-3,0). (1)、如图1,点O为坐标原点,⊙O的半径是3,点P是点A关于⊙O的“倍距点”.
(1)、如图1,点O为坐标原点,⊙O的半径是3,点P是点A关于⊙O的“倍距点”.①若点P在x轴正半轴上,则点P的坐标是 ;
②若点P在第一象限,且∠PAO=30°,求点P的坐标;
(2)、设点M(m,0),以点M为圆心,MA长为半径作⊙M,一次函数y= x+ 的图象分别与x轴、y轴交于D、E,若一次函数y= x+ 的图象上存在唯一一点P,使点P是点A关于⊙M的“倍距点”,请你直接写出m的值.26. 在 中, 点 为 边上的动点,速度为 .

 (1)、如图1,点 为 边上一点, ,动点 从点 出发,在 的边上沿 的路径匀速运动,当到达点 时停止运动.设 的面积为 的面积为 ,点 运动的时间为 与 之间的函数关系如图2所示,根据题意解答下列问题:
(1)、如图1,点 为 边上一点, ,动点 从点 出发,在 的边上沿 的路径匀速运动,当到达点 时停止运动.设 的面积为 的面积为 ,点 运动的时间为 与 之间的函数关系如图2所示,根据题意解答下列问题:①在图1中, ▲ ▲ ;
②在图2中,求 和 的交点 的坐标;
(2)、在(1)的条件下,如图3,若点 ,点 同时从点 出发,在 的边上沿 的路径匀速运动,点 运动的速度为 ,当点 到达点 时,点 与点 同时停止运动.求 为何值时, 最大?最大值为多少?27. 在平面直角坐标系 中,点M的坐标为 ,点N的坐标为 ,且 , ,若 , 为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点 , 的“标准矩形”,如图为点 , 的“标准矩形”示意图. (1)、已知点 的坐标为 ,
(1)、已知点 的坐标为 ,①点 为直线 图象上第一象限内的一点,且点 , 的“标准矩形”的两邻边长的比为1∶2,求点 的坐标;
②点 在直线 上,若点 , 的“标准矩形”为正方形,求直线 的表达式;
(2)、 的半径为2,点 的坐标为 ,若在 上存在一点 ,使得点 , 的“标准矩形”为正方形,直接写出 的取值范围.28. 如图①,甲,乙都是高为6米的长方体容器,容器甲的底面 是正方形,容器乙的底面 是矩形.如图②,已知正方形 与矩形 满足如下条件:正方形 外切于一个半径为5米的圆 ,矩形 内接于这个圆 , .
 (1)、求容器甲,乙的容积分别为多少立方米?(2)、现在我们分别向容器甲,乙同时持续注水(注水前两个容器是空的),一开始注水流量均为25立方米/小时,4小时后.把容器甲的注水流量增加 立方米/小时,同时保持容器乙的注水流量不变,继续注水2小时后,把容器甲的注水流量再一次增加50立方米/小时,同时容器乙的注水流量仍旧保持不变.直到两个容器的水位高度相同,停止注水.在整个注水过程中,当注水时间为 时,我们把容器甲的水位高度记为 ,容器乙的水位高度记为 ,设 ,已知 (米)关于注水时间 (小时)的函数图象如图③所示,其中 平行于横轴.根据图中所给信息,解决下列问题:
(1)、求容器甲,乙的容积分别为多少立方米?(2)、现在我们分别向容器甲,乙同时持续注水(注水前两个容器是空的),一开始注水流量均为25立方米/小时,4小时后.把容器甲的注水流量增加 立方米/小时,同时保持容器乙的注水流量不变,继续注水2小时后,把容器甲的注水流量再一次增加50立方米/小时,同时容器乙的注水流量仍旧保持不变.直到两个容器的水位高度相同,停止注水.在整个注水过程中,当注水时间为 时,我们把容器甲的水位高度记为 ,容器乙的水位高度记为 ,设 ,已知 (米)关于注水时间 (小时)的函数图象如图③所示,其中 平行于横轴.根据图中所给信息,解决下列问题:①求 的值;
②求图③中线段 所在直线的解析式.