江西省高安市2022年中考第一次模拟数学试题
试卷更新日期:2022-04-15 类型:中考模拟
一、单选题
-
1. ﹣2的倒数是( )A、2 B、1 C、- D、2. 如图,几何体的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 第七次人口普查显示,高安市常住人口约为740000人,将数据740000用科学记数法表示为( )A、74×104 B、7.4×105 C、0.74×106 D、7.4×1074. 如图,与 , , 分别交于点E,G,F,且 , , 则下列结论不正确的是( )
3. 第七次人口普查显示,高安市常住人口约为740000人,将数据740000用科学记数法表示为( )A、74×104 B、7.4×105 C、0.74×106 D、7.4×1074. 如图,与 , , 分别交于点E,G,F,且 , , 则下列结论不正确的是( )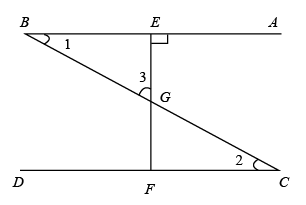 A、 B、 C、 D、5. 如图,是一个小正方体的展开图,把展开图折叠成小正方体后,有“三”字一面的相对面上的字是( )
A、 B、 C、 D、5. 如图,是一个小正方体的展开图,把展开图折叠成小正方体后,有“三”字一面的相对面上的字是( )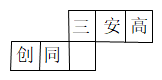 A、高 B、同 C、创 D、安6. 若将抛物线平移,有一个点既在平移前的抛物线上,又在平移后的抛物线上,则称这个点为“平衡点”.现将抛物线C1:向右平移m(m>0)个单位长度后得到新的抛物线C2 , 若(4,n)为“平衡点”,则m的值为( )A、2 B、1 C、4 D、3
A、高 B、同 C、创 D、安6. 若将抛物线平移,有一个点既在平移前的抛物线上,又在平移后的抛物线上,则称这个点为“平衡点”.现将抛物线C1:向右平移m(m>0)个单位长度后得到新的抛物线C2 , 若(4,n)为“平衡点”,则m的值为( )A、2 B、1 C、4 D、3二、填空题
-
7. 利用完全平方公式计算:(m+3)2= .8. 若关于 的方程 的一个根为3,则 的值为.9. 因式分解:x2﹣4= .10. 中国古代的算筹计数法可追溯到公元前5世纪.摆法有纵式和横式两种(如图所示),以算筹计数的方法是摆个位为纵,十位为横,百位为纵,千位为横……这样纵横依次交替,宋代以后出现了笔算,在个位数划上斜线以表示负数,如
 表示 ,
表示 ,  表示2369,则
表示2369,则 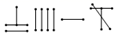 表示.
表示.  11. 如图,一次函数的图象与x轴、y轴分别交于点A,B,把直线AB绕点B顺时针旋转30°交x轴于点C,则线段AC长为 .
11. 如图,一次函数的图象与x轴、y轴分别交于点A,B,把直线AB绕点B顺时针旋转30°交x轴于点C,则线段AC长为 . 12. 如图,在Rt△ABC中,∠C=90°,∠B=30°,BC=12,点D为BC的中点,点E为AB上一点,把△BDE沿DE翻折得到△FDE,若FE与△ABC的直角边垂直,则BE的长为 .
12. 如图,在Rt△ABC中,∠C=90°,∠B=30°,BC=12,点D为BC的中点,点E为AB上一点,把△BDE沿DE翻折得到△FDE,若FE与△ABC的直角边垂直,则BE的长为 .
三、解答题
-
13. 计算:(1)、;(2)、14. 解不等式组并把解表示在数轴上.
 15. 根据省教育厅《关于认真做好2022年初中毕业生升学体育考试工作的通知》精神,凡报考我市普通高中、中等职业学校、五年制高职的应届、往届初中毕业生,均须参加2022年初中毕业升学体育考试,考试项目分为必考项目和选考项目,必考项目含男生1000米跑,女生800米跑;选考项目由考上从七个项目中任选2项,男生选考项目含50米跑、立定跳远、投掷实心球、引体向上、篮球运球、足球运球、排球垫球,女生选考项目含50米跑、立定跳远、一分钟仰卧起坐、引体向上、篮球运球、足球运球、排球垫球.小康决定从50米跑、立定跳远、投掷实心球(分别用A,B,C表示)选2项考试,每个项目选到的可能性相同(1)、“小康选到引体向上”是事件;(2)、请用列表或画树状图的方法,求小康选到50米跑、立定跳远的概率.16. 已知△ABC的顶点A、B、C在边长为1的网格格点上.
15. 根据省教育厅《关于认真做好2022年初中毕业生升学体育考试工作的通知》精神,凡报考我市普通高中、中等职业学校、五年制高职的应届、往届初中毕业生,均须参加2022年初中毕业升学体育考试,考试项目分为必考项目和选考项目,必考项目含男生1000米跑,女生800米跑;选考项目由考上从七个项目中任选2项,男生选考项目含50米跑、立定跳远、投掷实心球、引体向上、篮球运球、足球运球、排球垫球,女生选考项目含50米跑、立定跳远、一分钟仰卧起坐、引体向上、篮球运球、足球运球、排球垫球.小康决定从50米跑、立定跳远、投掷实心球(分别用A,B,C表示)选2项考试,每个项目选到的可能性相同(1)、“小康选到引体向上”是事件;(2)、请用列表或画树状图的方法,求小康选到50米跑、立定跳远的概率.16. 已知△ABC的顶点A、B、C在边长为1的网格格点上.
⑴画△ABC绕点O逆时针旋转90°得到的△A1B1C1;
⑵画△A1B1C1关于点O的中心对称图形△A2B2C2;
17. 政府为应对新冠疫情,促进经济发展,对商家打折销售进行了补贴,不打折时,6个A商品,5个B商品,总费用为114元,3个A商品,7个B商品,总费用为111元,打折后,小明购买了9个A商品和8个B商品共用了141.6元.(1)、求出商品A,B每个的标价;(2)、若商品A,B的折扣相同,商店打几折出售这两商品?小明在此次购物中得到了多少优惠?18. 如图,一次函数 的图象与反比例函数 的图象交于点 ,与 轴交于点 ,过点 作 轴,垂足为 ,若 .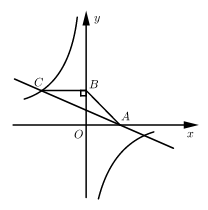 (1)、求点 的坐标及 的值;(2)、若 ,求一次函数的表达式.19. 每年都有很多人因火灾丧失生命,某校为提高学生的逃生意识,开展了“防火灾,爱生命”的防火灾知识竞赛,现从该校七、八年级中各抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用x表示,共分成四组:A: , B: , C: , D:),下面给出了部分信息:
(1)、求点 的坐标及 的值;(2)、若 ,求一次函数的表达式.19. 每年都有很多人因火灾丧失生命,某校为提高学生的逃生意识,开展了“防火灾,爱生命”的防火灾知识竞赛,现从该校七、八年级中各抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用x表示,共分成四组:A: , B: , C: , D:),下面给出了部分信息:七年级抽取的10名学生的竞赛成绩是:100,81,84,83,90,89,89,98,97,99;
八年级抽取的10名学生的竞赛成绩是:100,80,85,83,90,95,92,93,93,99;
【七、八年级抽取的学生竞赛成绩统计表】
年级
平均分
中位数
众数
方差
七年级
91
a
89
45.2
八年级
91
92.5
b
39.2
八年级抽取的学生竞赛成绩频数分布直方图

请根据相关信息,回答以下问题:
(1)、直接写出表格中a,b的值并补全八年级抽取的学生竞赛成绩频数分布直方图:(2)、根据以上数据,你认为该校七、八年级中哪个年级学生掌握防火安全知识较好?请说明理由(一条理由即可);(3)、该校七年级有800人,八年级有1000人参加了此次竞赛活动,请估计参加此次竞赛活动成绩优秀()的学生人数是多少.20. 长嘴壶茶艺表演是一项深受群众喜爱的民俗文化,是我国茶文化的一部分,所用到的长嘴壶更是历史悠久,源远流长.图①是现今使用的某款长嘴壶放置在水平桌面上的照片,图②是其抽象示意图,l是水平桌面,测得壶身AD=BC=3AE=24cm,AB=30cm,CD=22cm,且CD∥AB.壶嘴EF=80cm,∠FED=70°
参考数据:sin80°≈0.98,cos80°≈0.17,tan80°≈5.67,sin70°≈0.94,cos70°≈0.34,tan70°≈2.75.
(1)、求FE与水平桌面l的夹角(2)、如图③,若长嘴壶中装有若干茶水,绕点A转动壶身,当恰好倒出茶水时,EF∥l,求此时点F下落的高度.(结果保留一位小数).21. 如图,AB是⊙O的直径,E,C是⊙O上两点,且 , 连接AE,AC.过点C作CD⊥AE交AE的延长线于点D. (1)、判定直线CD与⊙O的位置关系,并说明理由;(2)、连接OE,连接BE交OC于F,若AB=4,CD= ,
(1)、判定直线CD与⊙O的位置关系,并说明理由;(2)、连接OE,连接BE交OC于F,若AB=4,CD= ,①求证:四边形DEFC是矩形;
②求图中阴影部分的面积.
22. 如图,在矩形ABCD中,AB=8,AD=4,点P是对角线BD上一点,连接AP,AE⊥AP,且= , 连接BE.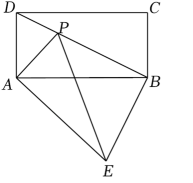 (1)、当DP=2时,求BE的长.(2)、四边形AEBP可能为矩形吗?如果不可能,请说明理由;如果可能,求出此时四边形AEBP的面积.23. 定义:点P(m,m)是平面直角坐标系内一点,将函数l的图象位于直线x=m左侧部分,以直线y=m为对称轴翻折,得到新的函数l′的图象,我们称函数l′的函数是函数l的相关函数,函数l′的图象记作F1 , 函数l的图象未翻折的部分记作F2 , 图象F1和F2合起来记作图象F.
(1)、当DP=2时,求BE的长.(2)、四边形AEBP可能为矩形吗?如果不可能,请说明理由;如果可能,求出此时四边形AEBP的面积.23. 定义:点P(m,m)是平面直角坐标系内一点,将函数l的图象位于直线x=m左侧部分,以直线y=m为对称轴翻折,得到新的函数l′的图象,我们称函数l′的函数是函数l的相关函数,函数l′的图象记作F1 , 函数l的图象未翻折的部分记作F2 , 图象F1和F2合起来记作图象F.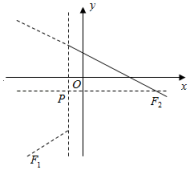
例如:函数l的解析式为y=x2﹣1,当m=1时,它的相关函数l′的解析式为y=﹣x2+3(x<1).
(1)、如图,函数l的解析式为y=﹣x+2,当m=﹣1时,它的相关函数l′的解析式为y= .(2)、函数l的解析式为y=﹣ , 当m=0时,图象F上某点的纵坐标为﹣2,求该点的横坐标.(3)、已知函数l的解析式为y=x2﹣4x+3,①已知点A、B的坐标分别为(0,2)、(6,2),图象F与线段AB只有一个公共点时,结合函数图象,求m的取值范围;
②若点C(x,n)是图象F上任意一点,当m﹣2≤x≤5时,n的最小值始终保持不变,求m的取值范围(直接写出结果).