山东省威海市2022年中考模拟数学试题二

试卷更新日期：2022-04-15 类型：中考模拟

进入出卷网下载

一、选择题

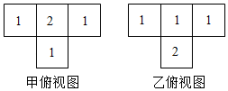
1. ﹣5的倒数是（）

A、﹣5 B、5 C、 $\frac{1}{5}$ D、 $- \frac{1}{5}$

查看试题解析
2. 甲和乙两个几何体都是由大小相同的小立方块搭成，它们的俯视图如图，小正方形中数字表示该位置上的小立方块个数，则下列说法中正确的是（）

A、甲和乙左视图相同，主视图相同 B、甲和乙左视图不相同，主视图不相同 C、甲和乙左视图相同，主视图不相同 D、甲和乙左视图不相同，主视图相同

查看试题解析
3. 2021年5月15日7时18分，天问一号探测器成功着陆距离地球逾3亿千米的神秘火星，在火星上首次留下中国人的印迹，这是我国航天事业发展的又一具有里程碑意义的进展.将数据3亿用科学记数法表示为（）

A、 $3 \times 10^{5}$ B、 $3 \times 10^{6}$ C、 $3 \times 10^{7}$ D、 $3 \times 10^{8}$

查看试题解析
4. 下列运算正确的是（）

A、 $2 x^{2} + 3 x^{3} = 5 x^{5}$ B、 ${(- 2 x)}^{3} = - 6 x^{3}$ C、 ${(x + y)}^{2} = x^{2} + y^{2}$ D、 $(3 x + 2) (2 - 3 x) = 4 - 9 x^{2}$

查看试题解析
5. 计算 $\frac{a^{2} - 4}{a}$ ÷（a+1﹣ $\frac{5 a - 4}{a}$ ）的结果是（）

A、 $\frac{a + 2}{a - 2}$ B、 $\frac{a - 2}{a + 2}$ C、 $\frac{(a - 2) (a + 2)}{a}$ D、 $\frac{a + 2}{a}$

查看试题解析
6. 在同一直角坐标系中，函数 $y = k x - k$ 与 $y = \frac{k}{| x |} (k \neq 0)$ 的大致图象是（）

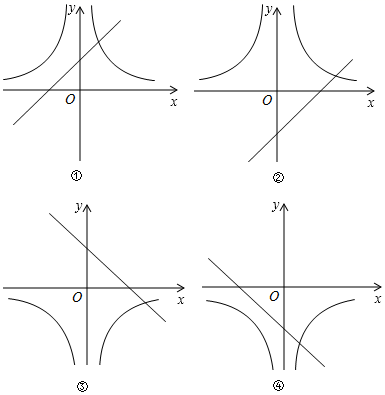A、①② B、②③ C、②④ D、③④

查看试题解析
7. 2020年以来，我国部分地区出现了新冠疫情．一时间，疫情就是命令，防控就是责任，一方有难八方支援，某公司在疫情期间为疫区生产A、B、C、D四种型号的帐篷共20000顶，有关信息见如下统计图：

下列判断正确的是（）

A、单独生产B型帐篷的天数是单独生产C型帐篷天数的3倍 B、单独生产B型帐篷的天数是单独生产A型帐篷天数的1.5倍 C、单独生产A型帐篷与单独生产D型帐篷的天数相等 D、每天单独生产C型帐篷的数量最多

查看试题解析
8. 如图，在平面直角坐标系中，菱形 $A B C D$ 的边 $A D ⊥ y$ 轴，垂足为E，顶点A在第二象限，顶点B在y轴正半轴上，反比例函数 $y = \frac{k}{x} (k \neq 0$ $， x > 0)$ 的图象同时经过顶点 $C 、 D$ ．若点C的横坐标为5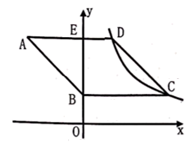， $B E = 2 D E$ ，则k的值为（）

A、 $\frac{40}{3}$ B、 $\frac{5}{2}$ C、 $\frac{5}{4}$ D、 $\frac{20}{3}$

查看试题解析
9. 七巧板起源于我国先秦时期，古算书《周髀算经》中有关于正方形的分割术，经历代演变而成七巧板，如图1所示.19世纪传到国外，被称为“唐图”（意为“来自中国的拼图”），图2是由边长为4的正方形分割制作的七巧板拼摆成的“叶问蹬”图.则图中抬起的“腿”（即阴影部分）的面积为（）

A、3 B、 $\frac{7}{2}$ C、2 D、 $\frac{5}{2}$

查看试题解析
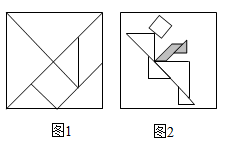10. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，有下列结论：① $a b c > 0$ ，② $4 a - 2 b + c < 0$ ，③ $a - b \geq x (a x + b)$ ，④ $3 a + c < 0$ ，正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
11. 如图，点 $E ， F$ 在矩形 $A B C D$ 的对角线 $B D$ 所在的直线上， $B E = D F$ ，则四边形 $A E C F$ 是（）

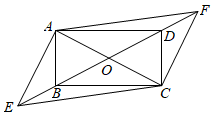A、平行四边形 B、矩形 C、菱形 D、正方形

查看试题解析
12. 在锐角△ABC中，∠A，∠B，∠C所对的边分别为a，b，c，有以下结论： $\frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC} = 2 R$ （其中R为△ABC的外接圆半径）成立.在△ABC中，若∠A=75°，∠B=45°，c=4，则△ABC的外接圆面积为（）

A、 $\frac{16 π}{3}$ B、 $\frac{64 π}{3}$ C、 $16 π$ D、 $64 π$

查看试题解析

二、填空题

13. 已知： $a = {(\frac{1}{2})}^{- 1} + {(- \sqrt{3})}^{0}$ ， $b = (\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})$ ，则 $\sqrt{a + b} =$ .

查看试题解析
14. 对于任意实数a、b，定义一种运算： $a \otimes b = a^{2} + b^{2} - a b$ ，若 $x \otimes (x - 1) = 3$ ，则x的值为.

查看试题解析
15. 如图1，在平面直角坐标系xOy中，抛物线y＝ax²+bx+c与x轴分别相交于A、B两点，与y轴相交于点C，下表给出了这条抛物线上部分点(x，y)的坐标值：
x
…
﹣1
0
1
2
3
…
y
…
0
3
4
3
0
…
则这条抛物线的解析式为．

查看试题解析
16. 如图，在平面直角坐标系中，正方形ABCD的顶点A在x轴正半轴上，顶点B，C在第一象限，顶点D的坐标 $(\frac{5}{2} ， 2)$ . 反比例函数 $y = \frac{k}{x}$ （常数 $k > 0$ ， $x > 0$ ）的图象恰好经过正方形ABCD的两个顶点，则k的值是.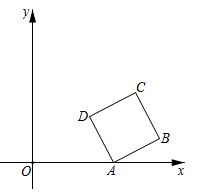

查看试题解析
17. 《九章算术》中记载了一种测量古井水面以上部分深度的方法．如图所示，在井口A处立一根垂直于井口的木杆 $A B$ ，从木杆的顶端B观察井水水岸D ，视线 $B D$ 与井口的直径 $A C$ 交于点E ，如果测得 $A B = 1$ 米， $A C = 1.6$ 米， $A E = 0.4$ 米，那么 $C D$ 为米．

查看试题解析
18. 如图，用火柴棍拼成一个由三角形组成的图形，拼第一个图形共需要3根火柴棍，拼第二个图形共需要5根火柴棍；拼第三个图形共需要7根火柴棍；……照这样拼图，则第n个图形需要根火柴棍.

查看试题解析

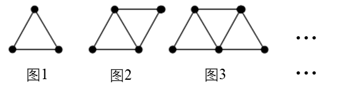
三、解答题

19. 解不等式组： ${\begin{array}{l} 2 x - 3 \leq 1 \\ \frac{x + 1}{3} > - 1 \end{array}$ ，并将解集在数轴上表示出来．

查看试题解析
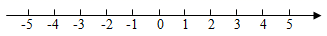20. “30天无理由退货”是营造我省“诚信旅游”良好环境，进一步提升旅游形象的创新举措．机场车站、出租车、景区、手机短信……，“30天无理由退货”的提示随处可见，它已成为一张云南旅行的“安心卡”，极大地提高了旅游服务的品质．刚刚过去的“五•一”假期，旅游线路、住宿、餐饮、生活服务、购物等旅游消费的供给更加多元，同步的是云南旅游市场强劲复苏．某旅行社今年5月1日租用A、B两种客房一天，供当天使用．下面是有关信息：
请根据上述信息，分别求今年5月1日该旅行社租用的A、B两种客房每间客房的租金．

查看试题解析
21. 随着科学技术的不断进步，无人机被广泛应用到实际生活中，小星利用无人机来测量广场 $B ， C$ 两点之间的距离.如图所示，小星站在广场的 $B$ 处遥控无人机，无人机在 $A$ 处距离地面的飞行高度是 $41 .6m$ ，此时从无人机测得广场 $C$ 处的俯角为 $63 °$ ，他抬头仰视无人机时，仰角为 $α$ ，若小星的身高 $B E = 1.6 m ， E A = 50 m$ （点 $A ， E ， B ， C$ 在同一平面内）.
$(\sin 63 ° \approx 0.89 ， \cos 63 ° \approx 0.45 ， \tan 63 ° \approx 1.96 ， \sin 27 ° \approx 0.45 ， \cos 27 ° \approx 0.89 ， \tan 27 ° \approx 0.51)$

(1)、求仰角 $α$ 的正弦值；

(2)、求 $B ， C$ 两点之间的距离（结果精确到 $1m$ ）.

查看试题解析
22. 如图，已知 $△$ ABC内接于⊙O，AB是⊙O的直径，∠CAB的平分线交BC于点D，交⊙O于点E，连接EB，作∠BEF＝∠CAE，交AB的延长线于点F．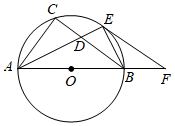

(1)、求证：EF是⊙O的切线；

(2)、若BF＝10，EF＝20，求⊙O的半径和AD的长．

查看试题解析
23. 一个不透明的箱子里装有3个红色小球和若干个白色小球，每个小球除颜色外其他完全相同，每次把箱子里的小球摇匀后随机摸出一个小球，记下颜色后再放回箱子里，通过大量重复实验后，发现摸到红色小球的频率稳定于0.75左右.

(1)、请你估计箱子里白色小球的个数；

(2)、现从该箱子里摸出1个小球，记下颜色后放回箱子里，摇匀后，再摸出1个小球，求两次摸出的小球颜色恰好不同的概率（用画树状图或列表的方法）.

查看试题解析
24. 如图，抛物线y=x²+bx+c与x轴相交于A，B两点，与y轴相交于点C，对称轴为直线x=2，顶点为D，点B的坐标为（3，0）．

(1)、填空：点A的坐标为，点D的坐标为，抛物线的解析式为．

(2)、当二次函数y=x²+bx+c的自变量x满足m≤x≤m+2时，函数y的最小值为 $\frac{5}{4}$ ，求m的值；

查看试题解析
25. 已知在 $△$ ABC中，O为BC边的中点，连接AO，将 $△$ AOC绕点O顺时针方向旋转（旋转角为钝角），得到 $△$ EOF，连接AE，CF.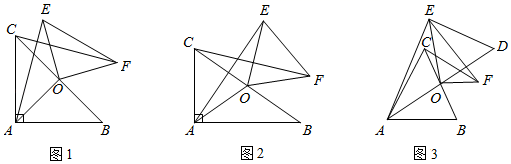

(1)、如图1，当∠BAC＝90°且AB＝AC时，则AE与CF满足的数量关系是；

(2)、如图2，当∠BAC＝90°且AB≠AC时，（1）中的结论是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由；

(3)、如图3，延长AO到点D，使OD＝OA，连接DE，当AO＝CF＝5，BC＝6时，求DE的长.

查看试题解析

x	…	﹣1	0	1	2	3	…
y	…	0	3	4	3	0	…