山西省吕梁市交城县2022年中考模拟试卷(一)数学试题
试卷更新日期:2022-04-15 类型:中考模拟
一、选择题
-
1. 下列各数中是无理数的是( )A、0 B、1.21 C、 D、2. 第二十四届冬季奥林匹克运动会于2022年2月20日在北京圆满落幕,中国体育健儿在本次运动会上取得了历史最好成绩,促进了全国冰雪运动的蓬勃发展.下面的图片都是冬奥会的会徽,上面有图案和文字说明,其中的图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 1968年科学家发现世界上最小的物质是夸克,物质就是由这种极其小的物质而构成的,夸克有多小呢?它的大小是1介米,约为原子核的百万分之一.百万分之一用科学记数法表示为( )A、1×10-5 B、1×10-6 C、1×106 D、1×10-84. 我国古代的数学家曾写下了许多数学名著,这些数学著作是了解古代数学成就的丰富宝库,其中有不少成就在世界范围内处于遥遥领先的地位.下列数学名著与其内容搭配不正确的一项是( )A、《周髀算经》 勾股定理 B、《九章算术》 负数的概念和正负数的运算 C、《海岛算经》 三斜求积术 D、《孙子算经》 鸡兔同笼5. 下列运算正确的是( )A、 B、 C、 D、6. 我国明代珠算家程大位的名著《直指算法统宗》里有一道著名算题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?如果译成白话文,其意思是:有100个和尚分100只馒头,正好分完.如果大和尚一人分3只,小和尚3人分一只,试问大、小和尚各有几人?设大和尚有人,则小和尚有(100-)人,根据题意列得方程( )A、3x+=100 B、3x+(100-x)=100 C、+3(100-x)=100 D、x+(100-x)=1007. 解分式方程时,去分母这一步方程两边不能同时乘以( )A、 B、 C、 D、8. 如图,在菱形ABCD中,∠ADC=120°,AB=4,连结AC,在AC上取一点F,使CF=CD,连结DF,则AF的长是( )
3. 1968年科学家发现世界上最小的物质是夸克,物质就是由这种极其小的物质而构成的,夸克有多小呢?它的大小是1介米,约为原子核的百万分之一.百万分之一用科学记数法表示为( )A、1×10-5 B、1×10-6 C、1×106 D、1×10-84. 我国古代的数学家曾写下了许多数学名著,这些数学著作是了解古代数学成就的丰富宝库,其中有不少成就在世界范围内处于遥遥领先的地位.下列数学名著与其内容搭配不正确的一项是( )A、《周髀算经》 勾股定理 B、《九章算术》 负数的概念和正负数的运算 C、《海岛算经》 三斜求积术 D、《孙子算经》 鸡兔同笼5. 下列运算正确的是( )A、 B、 C、 D、6. 我国明代珠算家程大位的名著《直指算法统宗》里有一道著名算题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?如果译成白话文,其意思是:有100个和尚分100只馒头,正好分完.如果大和尚一人分3只,小和尚3人分一只,试问大、小和尚各有几人?设大和尚有人,则小和尚有(100-)人,根据题意列得方程( )A、3x+=100 B、3x+(100-x)=100 C、+3(100-x)=100 D、x+(100-x)=1007. 解分式方程时,去分母这一步方程两边不能同时乘以( )A、 B、 C、 D、8. 如图,在菱形ABCD中,∠ADC=120°,AB=4,连结AC,在AC上取一点F,使CF=CD,连结DF,则AF的长是( )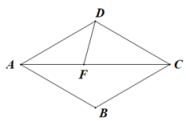 A、 B、 C、 D、9. 如图,正比例函数的图象经过点A(3,4),且与反比例函数的图象交于点B,C两点,点C是OA的中点,当时,的取值范围为( )
A、 B、 C、 D、9. 如图,正比例函数的图象经过点A(3,4),且与反比例函数的图象交于点B,C两点,点C是OA的中点,当时,的取值范围为( )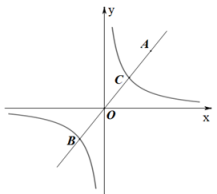 A、 B、 C、或 D、或10. 如图,正方形ABCD的边长是 , 以正方形对角线的一半OA为边作正六边形,其中一边与正方形的边CD交于点E,再以点O为圆心OE为半径画弧交AD于点F,则图中阴影部分的的面积为( )
A、 B、 C、或 D、或10. 如图,正方形ABCD的边长是 , 以正方形对角线的一半OA为边作正六边形,其中一边与正方形的边CD交于点E,再以点O为圆心OE为半径画弧交AD于点F,则图中阴影部分的的面积为( )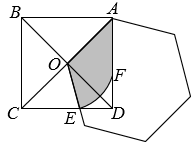 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 用配方法把二次函数化成顶点式为 .12. 不等式组的解集是 .13. 在平面直角坐标系中,△ABC和△DEF是以原点O为位似中心的位似图形,其位似比为1:3,那么点A(1,3)的对应点D的坐标为 .14. 如图,平面直角坐标系中,点A(1,2)、点C(4,4)是矩形ABCD的两个顶点,AB与轴平行,则直线与矩形公共部分的线段EF长为 .
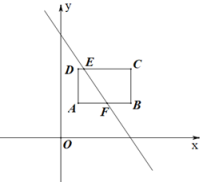 15. 如图,把△ABC绕着点A逆时针旋转90°得到△ADE,连接BE,CD,M是BE的中点,若AM= , 则CD的长为 .
15. 如图,把△ABC绕着点A逆时针旋转90°得到△ADE,连接BE,CD,M是BE的中点,若AM= , 则CD的长为 .
三、解答题
-
16.(1)、计算:÷sin45°.(2)、先化简,再求值: , 代入你喜欢的 , 值求结果.17. 我县某宾馆有若干间标准房,平时以市场管理部门批准的标价200元定价时(定价不得超过380元),平均每日可入住50间,在去年国庆黄金周中,为了增加营业额,该宾馆决定上调房价,经市场调查表明,定价每提高20元,每日入住房间数就减少1间,若不考虑其他因素,问国庆期间宾馆标准房的价格定为多少元时,每日的营业额可为11520元?18. 如图,△ABC内接于⊙O,AD与BC是⊙O的直径,延长线段AC至点G,使CG=AC,连接DG,点E在DG边上,并且∠ADG=2∠GCE.
 (1)、求证:CE是⊙O的切线;(2)、若AG=8,OA=5,求EG的长.19. 某校为了“中考体测”的顺利进行,引导同学们积极参加体育锻炼,学校购买了一批跳绳供学生借用,现从九年级随机抽取了部分学生对新跳绳进行测试,绘制了如下的两幅不完整的统计表和统计图.请根据相关信息,解答下列问题:
(1)、求证:CE是⊙O的切线;(2)、若AG=8,OA=5,求EG的长.19. 某校为了“中考体测”的顺利进行,引导同学们积极参加体育锻炼,学校购买了一批跳绳供学生借用,现从九年级随机抽取了部分学生对新跳绳进行测试,绘制了如下的两幅不完整的统计表和统计图.请根据相关信息,解答下列问题:一分钟跳绳成绩的分组统计表
组别
跳绳次数分段
频数
A
10
B
C
42
D
13
一分钟跳绳成绩的扇形统计图
 (1)、本次接受随机抽样调查的学生人数为人,统计表中的的值为;(2)、抽取学生一分钟跳绳成绩的中位数所在的组别是;(3)、现在指定两名男生和两名女生负责跳绳发放和整理工作,若两人一组,随机组合,则恰好分组都是一男一女的概率是多少?20. 阅读下列材料,并按要求完成相应的任务.
(1)、本次接受随机抽样调查的学生人数为人,统计表中的的值为;(2)、抽取学生一分钟跳绳成绩的中位数所在的组别是;(3)、现在指定两名男生和两名女生负责跳绳发放和整理工作,若两人一组,随机组合,则恰好分组都是一男一女的概率是多少?20. 阅读下列材料,并按要求完成相应的任务.黄金三角形与五角星
当等腰三角形的顶角为36°(或108°)时,它的底与腰的比(或腰与底的比)为 , 我们把这样的三角形叫做黄金三角形.
按下面的步骤画一个五角星(如图):
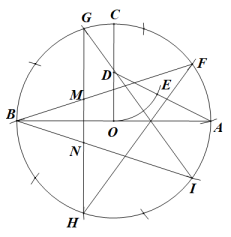
①作一个以AB为直径的圆,圆心为O;
②过圆心O作半径OC⊥AB;
③取OC的中点D,连接AD;
④以D为圆心OD为半径画弧交AD于点E;
⑤从点A开始以AE为半径顺时针依次画弧,
正好把⊙O十等分(其中点F,G,B,H,I为五等分点);
⑥以点F,G,B,H,I为顶点画出五角星.
任务:
(1)、求出的值为;(2)、如图,GH与BF,BI分别交于点M,N,求证:△BMN是黄金三角形.21. 如图,是放在水平桌面上的台灯的几何图,已知台灯底座高度为2cm,固定支点O到水平桌面的距离为7.5cm,当支架OA、AB拉直时所形成的线段与点M共线且与底座垂直,此时测得B到底座的距离为31.64cm(线段AB,AO,OM的和),经调试发现,当∠OAB=115°,∠AOM=160°时,台灯所投射的光线最适合写作业,测量得A到B的水平距离为10cm,求此时点B到桌面的距离.(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,)
 22. 综合与实践
22. 综合与实践问题情境
Rt△ABC和Rt△DEF如图1放置,点B与点D重合,∠ACB=∠EDF=90°,∠A=30°,AB=ED=FD=4,EF分别与AC,AB交于点N,点P,点M是AB的中点.
 (1)、数学思考
(1)、数学思考连接MN,求证:点N是EF的中点;并计算△MNP的面积;
(2)、操作探究如图2,先将△DEF沿BC的方向平移,使点D与点C重合,再沿CA的方向平移到点D为AC的中点时停止;过点C作CH∥AB交DE于点H,连接AH,AN,CM.试判断四边形AMCH的形状,并说明理由;
 (3)、在图2的基础上,将△DEF绕着点D顺时针旋转30°,CH∥AB仍然存在,延长CH交MN于点G,交EF于点Q,如图3.请直接写出三角形CMG的面积.
(3)、在图2的基础上,将△DEF绕着点D顺时针旋转30°,CH∥AB仍然存在,延长CH交MN于点G,交EF于点Q,如图3.请直接写出三角形CMG的面积. 23. 如图1,已知抛物线与轴交于A(-1,0),B两点,与轴交于点C(0,-2)连接BC.
23. 如图1,已知抛物线与轴交于A(-1,0),B两点,与轴交于点C(0,-2)连接BC. (1)、求抛物线的解析式与直线BC的解析式;(2)、点P是直线BC下方抛物线上一动点(不与B,C重合),当PD⊥BC于点D时,求出PD的最大值,并求此时点P的坐标;(3)、如图2,连接AC,抛物线的对称轴为直线EF,点M是直线EF右侧抛物线上一点,连接AM交EF于点Q,过点M作MN⊥EF于点N,是否存在这样的点M,使得△QMN与△ACO相似?若存在,请直接写出点M的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式与直线BC的解析式;(2)、点P是直线BC下方抛物线上一动点(不与B,C重合),当PD⊥BC于点D时,求出PD的最大值,并求此时点P的坐标;(3)、如图2,连接AC,抛物线的对称轴为直线EF,点M是直线EF右侧抛物线上一点,连接AM交EF于点Q,过点M作MN⊥EF于点N,是否存在这样的点M,使得△QMN与△ACO相似?若存在,请直接写出点M的坐标;若不存在,请说明理由.