广东省韶关市南雄市2021-2022学年九年级下学期 第一次质检数学试题
试卷更新日期：2022-04-15 类型：中考模拟
一、单选题
-
1. 下列交通标志中，既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
2. 下列事件中，是必然事件的是（ ）A、购买一张彩票，中奖 B、射击运动员射击一次，命中靶心 C、经过有交通信号灯的路口，遇到红灯 D、任意画一个三角形，其内角和是180°3. 反比例函数y＝的图象在（ ）A、第一、三象限 B、第二、四象限 C、第一、二象限 D、第三、四象限4. 把抛物线y=-2x2向上平移1个单位，再向右平移1个单位，得到的抛物线是（ ）A、 B、 C、 D、5. 方程x2－2x－1=0的根的情况是 （ ）
A、有两个不等实数根 B、有两个相等实数根 C、无实数根 D、无法判定6. 抛物线y＝（x﹣1）2﹣2的顶点坐标为（ ）A、（1，2） B、（1，﹣2） C、（﹣1，2） D、（﹣1，﹣2）7. 有一个正n边形的中心角是36°，则n为（ ）A、7 B、8 C、9 D、108. 如图，AB是⊙O的弦，OC⊥AB，交⊙O于点C，连接OA，OB，BC，若∠ABC＝20°，则∠AOB的度数是（ ）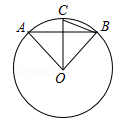
A、40° B、50° C、70° D、80°9. 设x1、x2是方程x2+3x﹣3=0的两个实数根，则+的值为（）A、5 B、﹣5 C、1 D、﹣110. 抛物线y＝ax2＋bx＋c的对称轴为直线x＝﹣1，部分图象如图所示，下列判断中：①abc＞0；②b2﹣4ac＞0；③9a﹣3b＋c＝0；④8a﹣2b＋c＞0；⑤若点（﹣0.5，y1），（﹣2，y2）均在抛物线上，则y1＞y2 ， 其中正确的有（ ）
A、②③④ B、①②③ C、②④⑤ D、②③二、填空题
-
11. 若x＝1是方程x2﹣4x＋m＝0的根，则m的值为 ．12. 某射击运动员在同一条件下的射击成绩记录如下：
射击次数
50
100
200
400
800
1000
“射中9环以上”的次数
38
82
157
317
640
801
“射中9环以上”的频率
0.760
0.820
0.785
0.793
0.800
0.801
根据频率的稳定性，估计这名运动员射击一次时“射中9环以上”的概率是 ． （结果保留小数点后一位）
13. 扇形的弧长为10πcm ， 面积为120πcm2 ， 则扇形的半径为cm ．14. 如图，△ABC以点O为旋转中心，旋转后得到 ， E、D分别是AB、AC的中点，经旋转后对应点分别为 ， 已知BC＝4，则等于 ．
15. 如图，△ABC 内接于⊙O，∠A＝72°，则∠OBC＝ ．
16. 如果点A（﹣3，2m＋1）关于原点对称的点在第一象限，则m的取值范围是 ．17. 如图，点A是反比例函数图象上的一点，过点A作AC⊥x轴，垂足为点C，D为AC的中点，若△AOD的面积为1，则k的值为 ．
三、解答题
-
18. 解下列方程：(1)、x2﹣x＝2（x﹣1）(2)、x2＋6x﹣1＝019. 在如图所示的直角坐标系中，解答下列问题：
(1)、分别写出A、B两点的坐标；(2)、将△ABC绕点A顺时针旋转90°，画出旋转后的△AB1C120. 如图，PA、PB是⊙O的切线，A、B为切点，AC是⊙O的直径，∠P=50°，求∠BAC的度数．
21. 一个盒中有4个完全相同的小球，把它们分别标号为1，2，3，4，随机摸取一个小球然后放回，再随机摸出一个小球．（Ⅰ）请用列表法（或画树状图法）列出所有可能的结果；
（Ⅱ）求两次取出的小球标号相同的概率；
（Ⅲ）求两次取出的小球标号的和大于6的概率．
22. 某水果批发商经销一种水果，进货价是12元/千克，如果销售价定为22元/千克，每日可售出500千克；经市场调查发现，在进货价不变的情况下，若每千克涨价1元，日销售量将减少20千克．(1)、若要每天销售盈利恰好为6000元，同时又可使顾客得到实惠，每千克应涨价为多少元？(2)、当销售价是多少时，每天的盈利最多？最多是多少？23. 如图，一次函数y=x+4的图象与反比例函数y= （k为常数且k≠0）的图象交于A（﹣1，a），B两点，与x轴交于点C．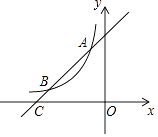
(1)、求此反比例函数的表达式；(2)、若点P在x轴上，且S△ACP=S△BOC ， 求点P的坐标．
