云南省2022年初中学业水平考试模拟数学试题
试卷更新日期:2022-04-15 类型:中考模拟
一、单选题
-
1. 某种食品保存的温度是-2±2℃,以下几个温度中,适合储存这种食品的是( )A、1℃ B、-8℃ C、4℃ D、-1℃2. 如图,直线a,b被直线c所截,a∥b,∠1=50°,则∠2的度数为( )
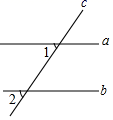 A、40° B、50° C、130° D、150°3. 对于任意实数k,关于x的方程 的根的情况为( )A、有两个相等的实数根 B、没有实数根 C、有两个不相等的实数根 D、无法判定4. 如图,在 中, ,D是 的中点, ,交 的延长线于点E . 若 , ,则 的长为( )
A、40° B、50° C、130° D、150°3. 对于任意实数k,关于x的方程 的根的情况为( )A、有两个相等的实数根 B、没有实数根 C、有两个不相等的实数根 D、无法判定4. 如图,在 中, ,D是 的中点, ,交 的延长线于点E . 若 , ,则 的长为( ) A、 B、 C、 D、5. 如图,小明从A点出发,沿直线前进8米后向左转45°,再沿直线前进8米,又向左转45°…照这样走下去,他第一次回到出发点A时,共走路程为( )
A、 B、 C、 D、5. 如图,小明从A点出发,沿直线前进8米后向左转45°,再沿直线前进8米,又向左转45°…照这样走下去,他第一次回到出发点A时,共走路程为( )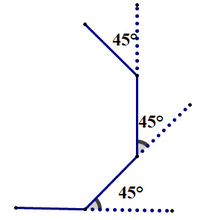 A、80米 B、96米 C、64米 D、48米6. 如图,在△ABC中,∠B=30°,AC=2,cosC= , 则AB的长为( )
A、80米 B、96米 C、64米 D、48米6. 如图,在△ABC中,∠B=30°,AC=2,cosC= , 则AB的长为( )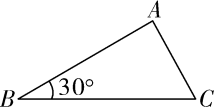 A、 B、 C、 D、7. 数形结合是解决数学问题常用的思想方法.如图,直线y=x+5和直线y=ax+b,相交于点P ,根据图象可知,方程x+5=ax+b的解是( )
A、 B、 C、 D、7. 数形结合是解决数学问题常用的思想方法.如图,直线y=x+5和直线y=ax+b,相交于点P ,根据图象可知,方程x+5=ax+b的解是( )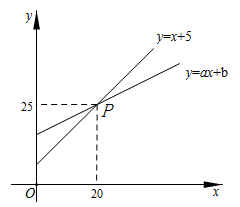 A、x=20 B、x=5 C、x=25 D、x=158. 如图, 是 的直径, 是弦,点 在直径 的两侧.若 , ,则 的长为( )
A、x=20 B、x=5 C、x=25 D、x=158. 如图, 是 的直径, 是弦,点 在直径 的两侧.若 , ,则 的长为( ) A、 B、 C、 D、9. 观察一列数: , …,按此规律,这一列数的第2022个数是( )A、 B、 C、 D、10. 如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A、 B、 C、 D、9. 观察一列数: , …,按此规律,这一列数的第2022个数是( )A、 B、 C、 D、10. 如图,若△ABC≌△ADE,则下列结论中一定成立的是( )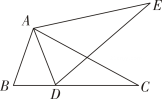 A、AC=DE B、∠BAD=∠CAE C、AB=AE D、∠ABC=∠AED11. 党的十八大以来,党中央把脱贫攻坚摆到更加突出的位置,根据国家统计局发布的数据,年年末全国农村贫困人口的情况如图所示,根据图中提供的信息,下列说法不正确的是( )
A、AC=DE B、∠BAD=∠CAE C、AB=AE D、∠ABC=∠AED11. 党的十八大以来,党中央把脱贫攻坚摆到更加突出的位置,根据国家统计局发布的数据,年年末全国农村贫困人口的情况如图所示,根据图中提供的信息,下列说法不正确的是( )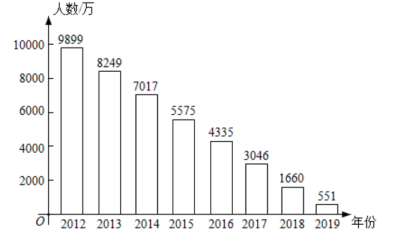 A、2019年末,农村贫困人口比上年末减少551万人 B、2012年末至2019年末,农村贫困人口累计减少超过9000万人 C、2012年末至2019年末,连续7年每年农村贫困人口减少1000万人以上 D、为在2020年末农村贫困人口全部脱贫,今年要确保完成减少551万农村人口的任务12. 若定义一种新运算: 例如: ; .则函数 的图象大致是( )A、
A、2019年末,农村贫困人口比上年末减少551万人 B、2012年末至2019年末,农村贫困人口累计减少超过9000万人 C、2012年末至2019年末,连续7年每年农村贫困人口减少1000万人以上 D、为在2020年末农村贫困人口全部脱贫,今年要确保完成减少551万农村人口的任务12. 若定义一种新运算: 例如: ; .则函数 的图象大致是( )A、 B、
B、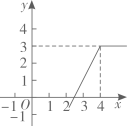 C、
C、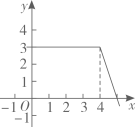 D、
D、
二、填空题
-
13. 已知a,b都是实数.若 , 则a+b= .14. 把多项式 分解因式的结果是 .15. 如图,若反比例函数y= (x<0)的图象经过点A , AB⊥x轴于B , 且△AOB的面积为6,则k= .
 16. 如图,在扇形OAB中,已知∠AOB=90°,OA= , 过的中点C作CD⊥OA,CE⊥OB,垂足分别为D、E,则图中阴影部分的面积为 .
16. 如图,在扇形OAB中,已知∠AOB=90°,OA= , 过的中点C作CD⊥OA,CE⊥OB,垂足分别为D、E,则图中阴影部分的面积为 . 17. 如图是一个几何体的三视图,则该几何体的体积为 .
17. 如图是一个几何体的三视图,则该几何体的体积为 . 18. 在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A出发向B以2cm秒的速度移动;点Q沿DA边从点D开始向A以1cm/秒的速度移动.如果P、Q同时出发,用t秒表示移动的时间(0<x<6)那么,当t为何值时,以点Q、A、P为顶点的三角形与ABC相似? .
18. 在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A出发向B以2cm秒的速度移动;点Q沿DA边从点D开始向A以1cm/秒的速度移动.如果P、Q同时出发,用t秒表示移动的时间(0<x<6)那么,当t为何值时,以点Q、A、P为顶点的三角形与ABC相似? .三、解答题
-
19. 每年的4月15日是我国全民国家安全教育日.某中学在全校七、八年级共800名学生中开展“国家安全法”知识竞赛,并从七、八年级学生中各抽取20名学生统计这部分学生的竞赛成绩(竞赛成绩均为整数,满分10分,6分及以上为合格).相关数据统计、整理如下:
八年级抽取的学生的竞赛成绩:
4,4,6,6,6,6,7,7,7,8,8,8,8,8,8,9,9,9,10,10.
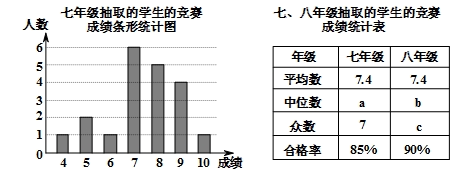
根据以上信息,解答下列问题:
(1)、填空:a= , b= , c= .(2)、估计该校七、八年级共800名学生中竞赛成绩达到9分及以上的人数;(3)、根据以上数据分析,从一个方面评价两个年级“国家安全法”知识竞赛的学生成绩谁更优异.20. 甲口袋中装有2个相同小球,它们分别写有数字1,2;乙口袋中装有3个相同小球,它们分别写有数字3,4,5;丙口袋中装有2个相同小球,它们分别写有数字6,7.从三个口袋各随机取出1个小球.用画树状图或列表法求:(1)、取出的3个小球上恰好有一个偶数的概率;(2)、取出的3个小球上全是奇数的概率.21. 如图,四边形ABCD为矩形,G是对角线BD的中点.连接GC并延长至F , 使CF=GC , 以DC , CF为邻边作菱形DCFE , 连接CE . (1)、判断四边形CEDG的形状,并证明你的结论;(2)、连接DF , 若BC= ,求DF的长.22. 受新冠肺炎疫情影响,一水果种植专业户有大量成熟水果无法出售.“一方有难,八方支援.”某水果经销商主动从该种植专业户购进甲,乙两种水果进行销售.专业户为了感谢经销商的援助,对甲种水果的出售价格根据购买量给予优惠,对乙种水果按25元/千克的价格出售.设经销商购进甲种水果x千克,付款y元,y与x之间的函数关系如图所示.
(1)、判断四边形CEDG的形状,并证明你的结论;(2)、连接DF , 若BC= ,求DF的长.22. 受新冠肺炎疫情影响,一水果种植专业户有大量成熟水果无法出售.“一方有难,八方支援.”某水果经销商主动从该种植专业户购进甲,乙两种水果进行销售.专业户为了感谢经销商的援助,对甲种水果的出售价格根据购买量给予优惠,对乙种水果按25元/千克的价格出售.设经销商购进甲种水果x千克,付款y元,y与x之间的函数关系如图所示.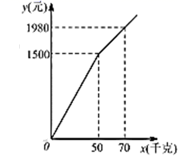 (1)、直接写出当 和 时,y与x之间的函数关系式;(2)、若经销商计划一次性购进甲,乙两种水果共100千克,且甲种水果不少于40千克,但又不超过60千克.如何分配甲,乙两种水果的则进量,才能使经销商付款总金额w(元)最少?(3)、若甲,乙两种水果的销售价格分别为40元/千克和36元/千克,经销商按(2)中甲,乙两种水果购进量的分配比例购进两种水果共a千克,且销售完a千克水果获得的利润不少于1650元,求a的最小值.23. 如图,点C在以AB为直径的⊙O上,BD平分∠ABC交⊙O于点D,过D作BC的垂线,垂足为E.
(1)、直接写出当 和 时,y与x之间的函数关系式;(2)、若经销商计划一次性购进甲,乙两种水果共100千克,且甲种水果不少于40千克,但又不超过60千克.如何分配甲,乙两种水果的则进量,才能使经销商付款总金额w(元)最少?(3)、若甲,乙两种水果的销售价格分别为40元/千克和36元/千克,经销商按(2)中甲,乙两种水果购进量的分配比例购进两种水果共a千克,且销售完a千克水果获得的利润不少于1650元,求a的最小值.23. 如图,点C在以AB为直径的⊙O上,BD平分∠ABC交⊙O于点D,过D作BC的垂线,垂足为E.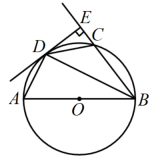 (1)、求证:DE与⊙O相切;(2)、若AB=5,BE=4,求BD的长;(3)、请用线段AB、BE表示CE的长,并说明理由.24. 已知直线l1:y=-2x+10交y轴于点A,交x轴于点B,二次函数的图象过A,B两点,交x轴于另一点C,BC=4,且对于该二次函数图象上的任意两点P1(x1 , y1),P2(x2 , y2),当x1>x2≥5时,总有y1>y2.(1)、求二次函数的表达式;(2)、若直线l2:y=mx+n(n≠10),求证:当m=-2时,l2//l1;(3)、E为线段BC上不与端点重合的点,直线l3:y=-2x+q过点C且交直线AE于点F,求与面积之和的最小值.
(1)、求证:DE与⊙O相切;(2)、若AB=5,BE=4,求BD的长;(3)、请用线段AB、BE表示CE的长,并说明理由.24. 已知直线l1:y=-2x+10交y轴于点A,交x轴于点B,二次函数的图象过A,B两点,交x轴于另一点C,BC=4,且对于该二次函数图象上的任意两点P1(x1 , y1),P2(x2 , y2),当x1>x2≥5时,总有y1>y2.(1)、求二次函数的表达式;(2)、若直线l2:y=mx+n(n≠10),求证:当m=-2时,l2//l1;(3)、E为线段BC上不与端点重合的点,直线l3:y=-2x+q过点C且交直线AE于点F,求与面积之和的最小值.