山西省2022年中考考前适应性训练(一模)数学试题
试卷更新日期:2022-04-15 类型:中考模拟
一、单选题
-
1. 下列各数:-4,-2.8,0, , 其中比-3小的数是( )A、-4 B、 C、0 D、-2.82. 党的十八大以来,坚持把教育扶贫作为脱贫攻坚的优先任务. 年,中央财政累计投入“全面改善贫困地区义务教育薄弱学校基本办学条件”专项补助资金1692亿元,将169200000000用科学记数法表示应为( )A、 B、 C、 D、3. 将如图所示的直棱柱展开,下列各示意图中不可能是它的表面展开图的是( )
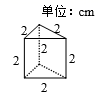 A、
A、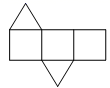 B、
B、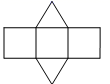 C、
C、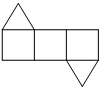 D、
D、 4. 下列运算正确的是( )A、 B、 C、 D、5. 若点 , , 都在反比例函的图象上,则 , , 的大小关系是( )A、 B、 C、 D、6. 为了保护环境加强环保教育,某中学组织学生参加义务收集废旧电池的活动,下面是随机抽取40名学生对收集废旧电池的数量进行的统计:
4. 下列运算正确的是( )A、 B、 C、 D、5. 若点 , , 都在反比例函的图象上,则 , , 的大小关系是( )A、 B、 C、 D、6. 为了保护环境加强环保教育,某中学组织学生参加义务收集废旧电池的活动,下面是随机抽取40名学生对收集废旧电池的数量进行的统计:废旧电池数/节
4
5
6
7
8
人数/人
9
11
11
5
4
请根据学生收集到的废旧电池数,判断下列说法正确的是( )
A、样本为40名学生 B、众数是11节 C、中位数是6节 D、平均数是5.6节7. 如图,在中, , 以点A为圆心,3为半径的圆与边相切于点D,与 , 分别交于点E和点G,点F是优弧上一点, , 则的度数是( )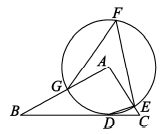 A、50° B、48° C、45° D、36°8. 某天早晨7:00,小明从家骑自行车去上学,途中因自行车发生故障,就地修车耽误了一段时间,修好车后继续骑行,7:30赶到了学校.图所示的函数图象反映了他骑车上学的整个过程.结合图象,判断下列结论正确的是( )
A、50° B、48° C、45° D、36°8. 某天早晨7:00,小明从家骑自行车去上学,途中因自行车发生故障,就地修车耽误了一段时间,修好车后继续骑行,7:30赶到了学校.图所示的函数图象反映了他骑车上学的整个过程.结合图象,判断下列结论正确的是( )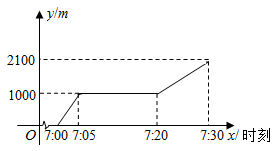 A、小明修车花了15min B、小明家距离学校1100m C、小明修好车后花了30min到达学校 D、小明修好车后骑行到学校的平均速度是3m/s9. 如图,正六边形 的边长为6,以顶点A为圆心, 的长为半径画圆,则图中阴影部分的面积为( )
A、小明修车花了15min B、小明家距离学校1100m C、小明修好车后花了30min到达学校 D、小明修好车后骑行到学校的平均速度是3m/s9. 如图,正六边形 的边长为6,以顶点A为圆心, 的长为半径画圆,则图中阴影部分的面积为( ) A、 B、 C、 D、10. 要得到抛物线 ,可以将抛物线 ( )A、向右平移6个单位长度,再向下平移3个单位长度 B、向右平移6个单位长度,再向上平移3个单位长度 C、向左平移6个单位长度,再向上平移3个单位长度 D、向左平移6个单位长度,再向下平移3个单位长度
A、 B、 C、 D、10. 要得到抛物线 ,可以将抛物线 ( )A、向右平移6个单位长度,再向下平移3个单位长度 B、向右平移6个单位长度,再向上平移3个单位长度 C、向左平移6个单位长度,再向上平移3个单位长度 D、向左平移6个单位长度,再向下平移3个单位长度二、填空题
-
11. 计算: .12. 如图,在平面直角坐标系中,菱形 对角线的交点坐标是 ,点 的坐标是 ,且 ,则点 的坐标是.
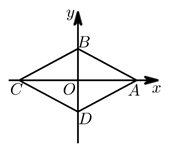 13. 已知一组数据:a、4、5、6、7的平均数为5,则这组数据的中位数是.14. 如图,四边形ABCD是⊙O的内接四边形,BE是⊙O的直径,连接AE.若∠BCD=2∠BAD,则∠DAE的度数是 .
13. 已知一组数据:a、4、5、6、7的平均数为5,则这组数据的中位数是.14. 如图,四边形ABCD是⊙O的内接四边形,BE是⊙O的直径,连接AE.若∠BCD=2∠BAD,则∠DAE的度数是 . 15. 如图,将三角形纸片 折叠,使点 、 都与点 重合,折痕分别为 、 .已知 , , ,则 的长为.
15. 如图,将三角形纸片 折叠,使点 、 都与点 重合,折痕分别为 、 .已知 , , ,则 的长为.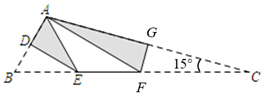
三、解答题
-
16.(1)、计算(2)、解不等式 .17. 2021年是中国共产党建党100周年,全国各地积极开展“弘扬红色文化,重走长征路”主题教育学习活动,我市“红二方面军长征出发地纪念馆”成为重要的活动基地.据了解,今年3月份该基地接待参观人数10万人,5月份接待参观人数增加到12.1万人.(1)、求这两个月参观人数的月平均增长率;(2)、按照这个增长率,预计6月份的参观人数是多少?18. 随着我国科技事业的不断发展,国产无人机大量进入快递行业.现有A,B两种型号的无人机都被用来运送快件,A型机比B型机平均每小时多运送20件,A型机运送700件所用时间与B型机运送500件所用时间相等,两种无人机平均每小时分别运送多少快件?19. 如图,大、小两个正方形的中心均与平面直角坐标系的原点O重合,边分别与坐标轴平行,反比例函数 的图象与大正方形的一边交于点A(1,2),且经过小正方形的顶点B.
 (1)、求反比例函数的解析式;(2)、求图中阴影部分的面积.20. 为庆祝中国共产党成立100周年,落实教育部《关于在中小学组织开展“从小学党史,永远跟党走”主题教育活动的通知》要求,某学校举行党史知识竞赛,随机调查了部分学生的竞赛成绩,绘制成两幅不完整的统计图表.根据统计图表提供的信息,解答下列问题:
(1)、求反比例函数的解析式;(2)、求图中阴影部分的面积.20. 为庆祝中国共产党成立100周年,落实教育部《关于在中小学组织开展“从小学党史,永远跟党走”主题教育活动的通知》要求,某学校举行党史知识竞赛,随机调查了部分学生的竞赛成绩,绘制成两幅不完整的统计图表.根据统计图表提供的信息,解答下列问题:
竞赛成绩统计表(成绩满分100分)
组别
分数
人数
A组
4
B组
C组
10
D组
E组
14
合计
(1)、本次共调查了名学生;C组所在扇形的圆心角为度;(2)、该校共有学生1600人,若90分以上为优秀,估计该校优秀学生人数为多少?(3)、若E组14名学生中有4人满分,设这4名学生为E1 , E2 , E3 , E4 , 从其中抽取2名学生代表学校参加上一级比赛,请用列表或画树状图的方法求恰好抽到 , 的概率.21. 图1是疫情期间测温员用“额温枪”对小红测温时的实景图,图2是其侧面示意图,其中枪柄 与手臂 始终在同一直线上,枪身 与额头保持垂直量得胳膊 , ,肘关节 与枪身端点 之间的水平宽度为 (即 的长度),枪身 .
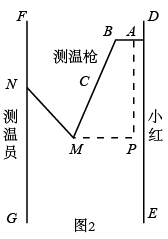
图1
(参考数据: , , , )
(1)、求 的度数;(2)、测温时规定枪身端点 与额头距离范围为 .在图2中,若测得 ,小红与测温员之间距离为 问此时枪身端点 与小红额头的距离是否在规定范围内?并说明理由.(结果保留小数点后一位)22.(1)、综合与实践如图1,AD为△ABC的角平分线, , 点E在AB上,AE=AC,求证:DE平分∠ADB.
 (2)、(思考探究)
(2)、(思考探究)如图2,在(1)的条件下,F为AB上一点,连结FC交AD于点G.若FB=FC,DG=2,CD=3,求BD的长.
 (3)、(拓展延伸)
(3)、(拓展延伸)如图3,在四边形ABCD中,对角线AC平分∠BAD,∠BCA=2∠DCA,点E在AC上,∠EDC=∠ABC.若BC=5, , AD=2AE,求AC的长.
 23. 如图,在平面直角坐标系中,抛物线的图象与坐标轴相交于A,B,C三点,其中A点坐标为 , B点坐标为 , 连接 , . 动点P从A点出发,在线段上以每秒个单位长度向点C做匀速运动;同时,动点Q从B点出发,在段上以每秒1个单位长度向点A做匀速运动,当其中一点到达终点时,另一点随之停止运动,连接 , 设运动时间为t秒.
23. 如图,在平面直角坐标系中,抛物线的图象与坐标轴相交于A,B,C三点,其中A点坐标为 , B点坐标为 , 连接 , . 动点P从A点出发,在线段上以每秒个单位长度向点C做匀速运动;同时,动点Q从B点出发,在段上以每秒1个单位长度向点A做匀速运动,当其中一点到达终点时,另一点随之停止运动,连接 , 设运动时间为t秒. (1)、b= , c=;(2)、在P,Q运动的过程中,当t为何值时,四边形的面积最小,最小值为多少?(3)、在线段上方的抛物线上是否存在点M,使是以点P为直角顶点的等腰直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
(1)、b= , c=;(2)、在P,Q运动的过程中,当t为何值时,四边形的面积最小,最小值为多少?(3)、在线段上方的抛物线上是否存在点M,使是以点P为直角顶点的等腰直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.