山东省烟台市2022年中考模拟数学试题

试卷更新日期：2022-04-15 类型：中考模拟

进入出卷网下载

一、单选题

1. 如果温度上升10℃记作+10℃，那么温度下降5℃记作（）

A、+10℃ B、﹣10℃ C、+5℃ D、﹣5℃

查看试题解析
2. 下列各式中，与 $2 a^{2} b$ 为同类项的是（）

A、 $- 2 a^{2} b$ B、 $- 2 a b$ C、 $2 a b^{2}$ D、 $2 a^{2}$

查看试题解析
3. 某市从2017年开始大力发展“竹文化”旅游产业．据统计，该市2017年“竹文化”旅游收入约为2亿元．预计2019“竹文化”旅游收入达到2.88亿元，据此估计该市2018年、2019年“竹文化”旅游收入的年平均增长率约为（）

A、2% B、4.4% C、20% D、44%

查看试题解析
4.
从棱长为2a的正方体零件的一角，挖去一个棱长为a的小正方体，得到一个如图所示的零件，则这个零件的俯视图是（）

A、 B、 C、 D、

查看试题解析
5. 不等式3（1﹣x）＞2﹣4x的解在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
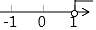6. 已知一个正多边形的内角是140°，则这个正多边形的边数是（　　）

A、6 B、7 C、8 D、9

查看试题解析
7. 已知m，n是一元二次方程 $x^{2} + x - 2021 = 0$ 的两个实数根，则代数式 $m^{2} + 2 m + n$ 的值等于（）

A、2019 B、2020 C、2021 D、2022

查看试题解析
8. 某校为了解学生的课外阅读情况，随机抽取了一个班级的学生，对他们一周的读书时间进行了统计，统计数据如下表所示：
读书时间（小时）
7
8
9
10
11
学生人数
6
10
9
8
7
则该班学生一周读书时间的中位数和众数分别是（）

A、9，8 B、9，9 C、9.5，9 D、9.5，8

查看试题解析
9. 如图，在 $△ A B C$ 中， $A B = B C$ ，由图中的尺规作图痕迹得到的射线 $B D$ 与 $A C$ 交于点E ，点F为 $B C$ 的中点，连接 $E F$ ，若 $B E = A C = 2$ ，则 $△ C E F$ 的周长为（）

A、 $\sqrt{3} + 1$ B、 $\sqrt{5} + 3$ C、 $\sqrt{5} + 1$ D、4

查看试题解析
10. 过三点A（2，2），B（6，2），C（4，5）的圆的圆心坐标为（）

A、（4， $\frac{17}{6}$ ） B、（4，3） C、（5， $\frac{17}{6}$ ） D、（5，3）

查看试题解析
11. 如图，PA、PB是⊙O的切线，切点分别为A、B ，若OA＝2，∠P＝60°，则 $\overset{⌢}{A B}$ 的长为（）

A、 $\frac{2}{3}$ π B、π C、 $\frac{4}{3} π$ D、 $\frac{5}{3} π$

查看试题解析
12. 已知二次函数y＝ax²+bx+c的自变量x与函数y的部分对应值见表格，则下列结论：①c＝2；②b²﹣4ac＞0；③方程ax²+bx＝0的两根为x₁＝﹣2，x₂＝0；④7a+c＜0.其中正确的有（）

x

…

﹣3

﹣2

﹣1

1

2

…

y

…

1.875

3

m

1.875

0

…

A、①④ B、②③ C、③④ D、②④

查看试题解析

二、填空题

13. 一个角是70°39′，则它的余角的度数是．

查看试题解析
14. 因式分解： $a^{2} - 9 =$ ．

查看试题解析
15. 如图，线段 $A B = 10 c m$ ，用尺规作图法按如下步骤作图．
⑴过点B作 $A B$ 的垂线，并在垂线上取 $B C = \frac{1}{2} A B$ ；
⑵连接 $A C$ ，以点C为圆心， $C B$ 为半径画弧，交 $A C$ 于点E；
⑶以点A为圆心， $A E$ 为半径画弧，交 $A B$ 于点D．即点D为线段 $A B$ 的黄金分割点．
则线段 $A D$ 的长度约为 $c m$ （结果保留两位小数，参考数据： $\sqrt{2} = 1.414 ， \sqrt{3} = 1.732 ， \sqrt{5} = 2.236$ ）

查看试题解析
16. 设 $A B$ ， $C D$ ， $E F$ 是同一平面内三条互相平行的直线，已知 $A B$ 与 $C D$ 的距离是 $12 c m$ ， $E F$ 与 $C D$ 的距离是 $5 c m$ ，则 $A B$ 与 $E F$ 的距离等于 $c m$ .

查看试题解析
17. 如图，在平面直角坐标系中，每个小方格的边长均为1， $Δ A O B$ 与 $Δ A^{'} O B^{'}$ 是以原点为位似中心的位似图形，且相似比为 $3 ： 2$ ，点 $A ， B$ 都在格点上，则点 $B^{'}$ 的坐标是.

查看试题解析
18. 如图，AB是⊙O的弦，AB＝5，点C是⊙O上的一个动点，且∠ACB＝45°，若点M、N分别是AB、AC的中点，则MN长的最大值是．

查看试题解析

三、解答题

19. 先化简，再求值： $\frac{x - 3}{x^{2} - 8 x + 16} \div \frac{x - 3}{x^{2} - 16} - \frac{x}{x - 4}$ ，其中 $x = \sqrt{2} + 4$

查看试题解析
20. 小云统计了自己所住小区5月1日至30日的厨余垃圾分出量（单位：千克），相关信息如下：
a．小云所住小区5月1日至30日的厨余垃圾分出量统计图：

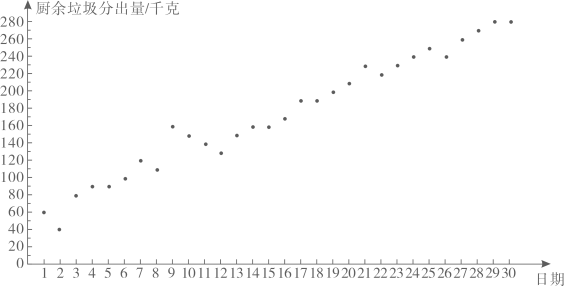
b．小云所住小区5月1日至30日分时段的厨余垃圾分出量的平均数如下：

时段

1日至10日

11日至20日

21日至30日

平均数

100

170

250

(1)、该小区5月1日至30日的厨余垃圾分出量的平均数约为（结果取整数）

(2)、已知该小区4月的厨余垃圾分出量的平均数为60，则该小区5月1日至30日的厨余垃圾分出量的平均数约为4月的倍（结果保留小数点后一位）；

(3)、记该小区5月1日至10日的厨余垃圾分出量的方差为 $s_{1}^{2} ，$ 5月11日至20日的厨余垃圾分出量的方差为 $s_{2}^{2}$ ，5月21日至30日的厨余垃圾分出量的方差为 $s_{3}^{2}$ ．直接写出 $s_{1}^{2} ， s_{2}^{2} ， s_{3}^{2}$ 的大小关系．

查看试题解析
21. 如图，在△ABC中，∠BAC＝90°，E为边BC上的点，且AB＝AE，D为线段BE的中点，过点E作EF⊥AE，过点A作AF∥BC，且AF、EF相交于点F.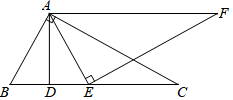

(1)、求证：∠C＝∠BAD；

(2)、求证：AC＝EF.

查看试题解析
22. 新冠疫情期间，口罩成为了人们出行必备的防护工具.某药店三月份共销售A，B两种型号的口罩9000只，共获利润5000元，其中A，B两种型号口罩所获利润之比为2：3.已知每只B型口罩的销售利润是A型口罩的1.2倍.

(1)、求每只A型口罩和B型口罩的销售利润；

(2)、该药店四月份计划一次性购进两种型号的口罩共10000只，其中B型口罩的进货量不超过A型口罩的1.5倍，设购进A型口罩m只，这10000只口罩的销售总利润为W元.该药店如何进货，才能使销售总利润最大？

查看试题解析
23. 如图，已知抛物线y=－x²+mx+3与x轴交于点A、B两点，与y轴交于C点，点B的坐标为（3，0），抛物线与直线y=－ $\frac{3}{2}$ x+3交于C、D两点.连接BD、AD.

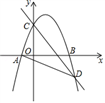(1)、求m的值.

(2)、抛物线上有一点P，满足S_△_ABP=4S_△_ABD ，求点P的坐标.

查看试题解析
24. 点P是平行四边形 $A B C D$ 的对角线 $A C$ 所在直线上的一个动点（点P不与点A、C重合），分别过点A、C向直线 $B P$ 作垂线，垂足分别为点E、F．点O为 $A C$ 的中点．

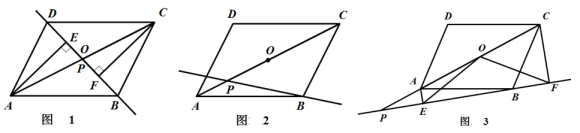(1)、如图1，当点P与点O重合时，线段OE和OF的关系是；

(2)、当点P运动到如图2所示的位置时，请在图中补全图形并通过证明判断（1）中的结论是否仍然成立？

(3)、如图3，点P在线段 $O A$ 的延长线上运动，当 $∠ O E F = 30 °$ 时，试探究线段 $C F$ 、 $A E$ 、 $O E$ 之间的关系．

查看试题解析
25. 如图，△ABC中，∠BAC为钝角，∠B=45°，点P是边BC延长线上一点，以点C为顶点，CP为边，在射线BP下方作∠PCF=∠B．

(1)、在射线CF上取点E，连接AE交线段BC于点D．
①如图1，若AD=DE，请直接写出线段AB与CE的数量关系和位置关系；
②如图2，若AD= $\sqrt{2}$ DE，判断线段AB与CE的数量关系和位置关系，并说明理由；

(2)、如图3，反向延长射线CF，交射线BA于点C′，将∠PCF沿CC′方向平移，使顶点C落在点C′处，记平移后的∠PCF为∠P′C′F′，将∠P′C′F′绕点C′顺时针旋转角α（0°＜α＜45°），C′F′交线段BC于点M，C′P′交射线BP于点N，请直接写出线段BM，MN与CN之间的数量关系．

查看试题解析

时段	1日至10日	11日至20日	21日至30日
平均数	100	170	250

读书时间（小时）	7	8	9	10	11
学生人数	6	10	9	8	7

x	…	﹣3	﹣2	﹣1	1	2	…
y	…	1.875	3	m	1.875	0	…