山东省聊城市东昌府区中考模拟考试(一)数学试题
试卷更新日期:2022-04-15 类型:中考模拟
一、单选题
-
1. 下列各数与互为相反数的是( )A、 B、 C、 D、2. 下面由8个完全相同的小正方体组成的几何体的左视图是( )
 A、
A、 B、
B、 C、
C、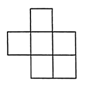 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 下列说法正确的是( )A、从小亮,小莹,小刚三人中抽1人参加诗歌比赛,小明被抽中是随机事件 B、要了解学校2000名学生的视力健康情况,随机抽取200名学生进行调查,在该调查中样本容量是200名学生 C、为了解人造卫星的设备零件的质量情况,应选择抽样调查 D、了解一批冰箱的使用寿命,采用抽样调查的方式5. 一块含有30°的直角三角板和直尺如图放置,若 , 则∠2的度数是( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 下列说法正确的是( )A、从小亮,小莹,小刚三人中抽1人参加诗歌比赛,小明被抽中是随机事件 B、要了解学校2000名学生的视力健康情况,随机抽取200名学生进行调查,在该调查中样本容量是200名学生 C、为了解人造卫星的设备零件的质量情况,应选择抽样调查 D、了解一批冰箱的使用寿命,采用抽样调查的方式5. 一块含有30°的直角三角板和直尺如图放置,若 , 则∠2的度数是( ) A、35° B、45° C、55° D、65°6. 下列计算正确的是( )A、 B、 C、 D、7. 如果不等式组的解集为 , 那么m的取值范围是( )A、 B、 C、 D、8. 已知在RtABC中, , , , 点D为边BC上的动点,点E为边AB上的中点,则线段的最小值是( )
A、35° B、45° C、55° D、65°6. 下列计算正确的是( )A、 B、 C、 D、7. 如果不等式组的解集为 , 那么m的取值范围是( )A、 B、 C、 D、8. 已知在RtABC中, , , , 点D为边BC上的动点,点E为边AB上的中点,则线段的最小值是( )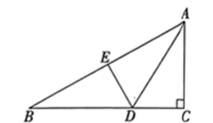 A、 B、 C、 D、9. 某通讯公司就上宽带网推出A,B,C三种月收费方式.这三种收费方式每月所需的费用y(元)与上网时间x(h)的函数关系如图所示,则下列判断不正确的是
A、 B、 C、 D、9. 某通讯公司就上宽带网推出A,B,C三种月收费方式.这三种收费方式每月所需的费用y(元)与上网时间x(h)的函数关系如图所示,则下列判断不正确的是 A、每月上网时间不足25h时,选择A方式最省钱 B、每月上网费用为60元时,B方式可上网的时间比A方式多 C、每月上网时间为35h时,选择B方式最省钱 D、每月上网时间超过70h时,选择C方式最省钱10. 如图,AB是⊙O的弦,圆心O到弦AB的距离 , 点C是弧AB中点,点D是优弧AB上的一点, , 则弦AB的长为( )
A、每月上网时间不足25h时,选择A方式最省钱 B、每月上网费用为60元时,B方式可上网的时间比A方式多 C、每月上网时间为35h时,选择B方式最省钱 D、每月上网时间超过70h时,选择C方式最省钱10. 如图,AB是⊙O的弦,圆心O到弦AB的距离 , 点C是弧AB中点,点D是优弧AB上的一点, , 则弦AB的长为( )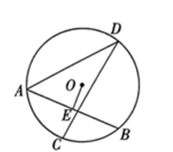 A、6 B、9 C、10 D、1211. 如图,在平面直角坐标系中,平行四边形OABC的顶点 , 点A在x轴的正半轴上,∠COA的平分线OD交BC于点 , 则点C的坐标为( )
A、6 B、9 C、10 D、1211. 如图,在平面直角坐标系中,平行四边形OABC的顶点 , 点A在x轴的正半轴上,∠COA的平分线OD交BC于点 , 则点C的坐标为( )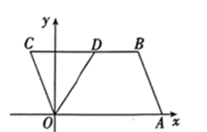 A、 B、 C、 D、12. 如图,已知抛物线(a,b,c为常数,)经过点 , 且对称轴为直线 , 有下列结论:
A、 B、 C、 D、12. 如图,已知抛物线(a,b,c为常数,)经过点 , 且对称轴为直线 , 有下列结论:①;②;③;④无论a,b,c取何值,抛物线一定经过;⑤ . 其中正确结论有( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
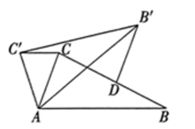
13. 因式分解:= .14. 若一个扇形的弧长是 , 面积是 , 由这个扇形所围成的圆锥的高是cm.15. 如图,在ABC中, , 在同一平面内,将ABC绕点A逆时针旋转到的位置,使 , 作交BC于点D,则 .
 16. 从标有数字1,2,3,4,5的五张卡片中,无放回地随机抽取两张,将抽取的卡片上的数字组成一个两位数,所组成的两位数的数字中为偶数的概率为 .17. 如图,直线与直线所成的角 , 过点作交直线于点 , , 以为边在外侧作等边三角形 , 再过点作 , 分别交直线和于 , 两点,以为边在外侧作等边三角形 , …按此规律进行下去,则第2022个等边三角形的周长为 .
16. 从标有数字1,2,3,4,5的五张卡片中,无放回地随机抽取两张,将抽取的卡片上的数字组成一个两位数,所组成的两位数的数字中为偶数的概率为 .17. 如图,直线与直线所成的角 , 过点作交直线于点 , , 以为边在外侧作等边三角形 , 再过点作 , 分别交直线和于 , 两点,以为边在外侧作等边三角形 , …按此规律进行下去,则第2022个等边三角形的周长为 .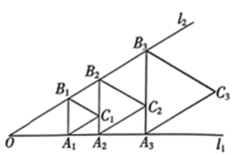
三、解答题
-
18. 先化简,再求值: , 其中 .19. “强我体魄,筑我精神”,某学校九年级在抓学生学习的同时,加强了学生的体育锻炼.为了解学生的体育锻炼情况,学校随机抽取30名男生进行引体向上的测试,成绩如下(单位:个):5 10 13 13 17 21 23 19 16 13 11 8 8 11 13 15 19 16 13 10 8 8 12 13 16 20 20 16 12 20,整理上面的数据得到频数分布表和频数分布直方图:
成绩(个)
频数
5
a
11
b
2
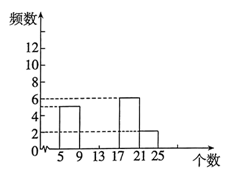
回答下列问题:
(1)、以上30个数据中,中位数是多少?频数分布表中a,b分别是多少?(2)、补全频数分布直方图;(3)、若成绩不低于13个为优秀,估计该校九年级300名学生中达到优秀等级的人数是多少?20. 已知菱形ABCD,E,F分别为菱形外的两点,且E,C,F三点共线,EF交AB于G,连接AE,DE,DF, , . 求证: .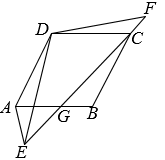 21. 我市某青少年素质教育实践基地,购买可重复使用的船模、航模器材,上学期采购船模器材共花费了2.88万元,采购航模器材共花费2.4万元,购进的船模器材的数量是购进的航模器材数量的 , 每个船模器材的价格比每个航模器材的价格少120元.(1)、求这两种器材的单价分别是多少元?(2)、本学期由于参加实践的学生人数增加,需要再购进这两种模型的器材50个,由于这两种器材的价格有所调整,每个船模器材的价格比上学期提高了5%,每个航模器材的价格比上学期降低了10%,若购买这两种器材的总费用不超过去年总费用的 , 那么最大可购进多少航模器材?22. 美丽的徒骇河穿城而过,成为市民休闲娱乐的风景带.某数学兴趣小组在一次课外活动中,测量徒骇河某段河的宽CD.如图所示,小组成员选取的点A,B是桥上的两点,点A,E,C在河岸的同一直线上,且 . 若 , 间的距离80米,在B点处测得与平行于AC的直线间的夹角为30°,在点E处测得ED与直线AC之间的夹角为60°,求这段河的宽度CD.(结果保留根号)
21. 我市某青少年素质教育实践基地,购买可重复使用的船模、航模器材,上学期采购船模器材共花费了2.88万元,采购航模器材共花费2.4万元,购进的船模器材的数量是购进的航模器材数量的 , 每个船模器材的价格比每个航模器材的价格少120元.(1)、求这两种器材的单价分别是多少元?(2)、本学期由于参加实践的学生人数增加,需要再购进这两种模型的器材50个,由于这两种器材的价格有所调整,每个船模器材的价格比上学期提高了5%,每个航模器材的价格比上学期降低了10%,若购买这两种器材的总费用不超过去年总费用的 , 那么最大可购进多少航模器材?22. 美丽的徒骇河穿城而过,成为市民休闲娱乐的风景带.某数学兴趣小组在一次课外活动中,测量徒骇河某段河的宽CD.如图所示,小组成员选取的点A,B是桥上的两点,点A,E,C在河岸的同一直线上,且 . 若 , 间的距离80米,在B点处测得与平行于AC的直线间的夹角为30°,在点E处测得ED与直线AC之间的夹角为60°,求这段河的宽度CD.(结果保留根号) 23. 如图,在平面直角坐标系中,一次函数的图象与x轴、y轴分别交于点A,B,且 , , 同时交反比例函数在第一象限的图象于点 , 反比例函数图象上的点P的纵坐标 , 轴交直线AB于点Q,D是x轴上任意一点,连接PD,QD.
23. 如图,在平面直角坐标系中,一次函数的图象与x轴、y轴分别交于点A,B,且 , , 同时交反比例函数在第一象限的图象于点 , 反比例函数图象上的点P的纵坐标 , 轴交直线AB于点Q,D是x轴上任意一点,连接PD,QD. (1)、求一次函数和反比例函数的表达式;(2)、求△PDQ面积的最大值.24. 如图,已知AB是⊙的直径,C,D分别为⊙上和⊙外的两点,连接AC,BC,连接DB并延长交AC的延长线于点H,作 , DG分别交AB,AC和⊙于点E、点G和点F,连接CF,若 .
(1)、求一次函数和反比例函数的表达式;(2)、求△PDQ面积的最大值.24. 如图,已知AB是⊙的直径,C,D分别为⊙上和⊙外的两点,连接AC,BC,连接DB并延长交AC的延长线于点H,作 , DG分别交AB,AC和⊙于点E、点G和点F,连接CF,若 .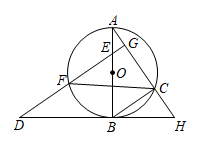 (1)、求证:BD与⊙相切;(2)、若 , 平分 , , 求DE的长.25. 如图,在平面直角坐标系中,直线与x轴,y轴相交于A,B两点,点C的坐标是 . 连接AC,BC.
(1)、求证:BD与⊙相切;(2)、若 , 平分 , , 求DE的长.25. 如图,在平面直角坐标系中,直线与x轴,y轴相交于A,B两点,点C的坐标是 . 连接AC,BC.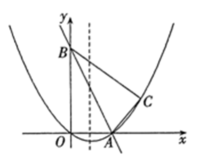 (1)、求过O,A,C三点的抛物线的函数表达式,并判断△ABC的形状;(2)、动点P从点O出发,沿OB以每秒2个单位长度的速度向点B运动;同时,动点Q从点B出发,沿BC以每秒1个单位长度的速度向点C运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为ts,当t为何值时,BPQ的面积最大?(3)、当抛物线的对称轴上有一点M,使以A,B,M为顶点的三角形是等腰三角形时,求出点M的坐标.
(1)、求过O,A,C三点的抛物线的函数表达式,并判断△ABC的形状;(2)、动点P从点O出发,沿OB以每秒2个单位长度的速度向点B运动;同时,动点Q从点B出发,沿BC以每秒1个单位长度的速度向点C运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为ts,当t为何值时,BPQ的面积最大?(3)、当抛物线的对称轴上有一点M,使以A,B,M为顶点的三角形是等腰三角形时,求出点M的坐标.