山东省济宁市金乡县2022年中考一模数学试题
试卷更新日期:2022-04-15 类型:中考模拟
一、单选题
-
1. 二次根式中的x取值范围是( )A、x≥-3 B、x≥3 C、x≥0 D、x≤-32. 点M(-4,3)关于x轴对称的点的坐标是( )A、(4,3) B、(-4,-3) C、(4,-3) D、(3,-4)3. “扶贫”是新时期党和国家的重点工作之一,为落实习近平总书记提出的“精准扶贫”战略构想,某省预计三年内脱贫1020000人,数字1020000用科学记数法可表示为( )A、1.02×106 B、1.02×105 C、10.2×105 D、102×1044. 不等式 的解集在数轴上表示,正确的是( )A、
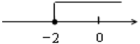 B、
B、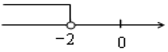 C、
C、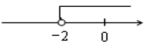 D、
D、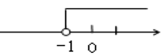 5. 如图,直线a、b被直线c所截.若∠1=55°,a∥b,则∠2的度数是( )
5. 如图,直线a、b被直线c所截.若∠1=55°,a∥b,则∠2的度数是( )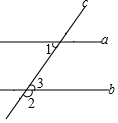 A、35° B、45° C、125° D、145°6. 数轴上点A表示的数是-2,将点A在数轴上移动6个单位长度得到点B,则点B表示的数是( )A、4 B、-4或8 C、-8 D、4或-87. 一组样本数据为1、2、3、3、6,下列说法不正确的是( )A、平均数是3 B、中位数是3 C、方差是3 D、众数是38. 如图,菱形ABCD的对角线AC,BD相交于点O,E为DC的中点,若OE=2,则菱形的周长为 ( )
A、35° B、45° C、125° D、145°6. 数轴上点A表示的数是-2,将点A在数轴上移动6个单位长度得到点B,则点B表示的数是( )A、4 B、-4或8 C、-8 D、4或-87. 一组样本数据为1、2、3、3、6,下列说法不正确的是( )A、平均数是3 B、中位数是3 C、方差是3 D、众数是38. 如图,菱形ABCD的对角线AC,BD相交于点O,E为DC的中点,若OE=2,则菱形的周长为 ( )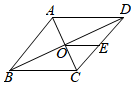 A、10 B、12 C、16 D、209. 如图,蒙古包可以近似地看作是由圆锥和圆柱组成,若用毛毡搭建一个底面半径为5米,圆柱高3米,圆锥高2米的蒙古包,则需要毛毡的面积为( )
A、10 B、12 C、16 D、209. 如图,蒙古包可以近似地看作是由圆锥和圆柱组成,若用毛毡搭建一个底面半径为5米,圆柱高3米,圆锥高2米的蒙古包,则需要毛毡的面积为( ) A、米2 B、米2 C、米2 D、米210. 如图,AB为⊙O的直径,AB=10,C,D为⊙O上两动点(C,D不与A,B重合),且CD为定长,CE⊥AB于E,M是CD的中点,则EM的最大值为( ).
A、米2 B、米2 C、米2 D、米210. 如图,AB为⊙O的直径,AB=10,C,D为⊙O上两动点(C,D不与A,B重合),且CD为定长,CE⊥AB于E,M是CD的中点,则EM的最大值为( ).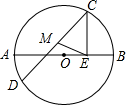 A、4 B、4.5 C、5 D、6
A、4 B、4.5 C、5 D、6二、填空题
-
11. 单项式 的次数.12. 图象经过点A(-2,6)的正比例函数y=kx,则k为 .13. 把多项式m3-16m分解因式的结果是 .14. 2021年3月25日,国家卫健委新闻发言人米锋在发布会上表示,疫情仍在全球扩散蔓延,但我国疫情已得到有效控制.新冠肺炎具有人传人的特性,若一人携带病毒,未进行有效隔离,经过两轮传染后共有169人患新冠肺炎(假设每轮传染的人数相同),则每轮传染中平均每个人传染了人.
三、解答题
-
15. 如图,已知等边三角形ABC绕点B顺时针旋转60°得△BCD,点E、F分别为线段AC和线段CD上的动点,若AE=CF,下列结论正确的有个.
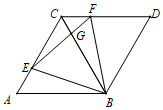
①四边形ABDC为菱形;②△ABE≌△CBF;③△BEF为等边三角形;④∠CFB=∠CGE;⑤若CE=3,CF=1,则BG= .
16.(1)、计算:;(2)、解方程: .17. 如图,在中,∠C=90°.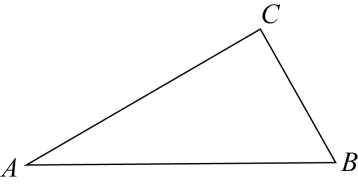 (1)、作∠BAC的平分线AD交边BC于点D.(尺规作图,保留作图痕迹,不写作法)(2)、在(1)的条件下,若∠BAC=38°,求∠ADB的度数.18. 随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)、作∠BAC的平分线AD交边BC于点D.(尺规作图,保留作图痕迹,不写作法)(2)、在(1)的条件下,若∠BAC=38°,求∠ADB的度数.18. 随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题: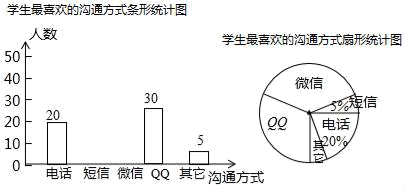 (1)、这次统计共抽查了名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为;(2)、将条形统计图补充完整;(3)、某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选中同一种沟通方式的概率.说明:设“微信,QQ和电话”三种沟通方式分别用字母W,Q和D表示.)19. 如图,AB与⊙O相切于点B,AO交⊙O于点C,AO的延长线交⊙O于点D,E是上不与B,D重合的点,sinA= .
(1)、这次统计共抽查了名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为;(2)、将条形统计图补充完整;(3)、某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选中同一种沟通方式的概率.说明:设“微信,QQ和电话”三种沟通方式分别用字母W,Q和D表示.)19. 如图,AB与⊙O相切于点B,AO交⊙O于点C,AO的延长线交⊙O于点D,E是上不与B,D重合的点,sinA= .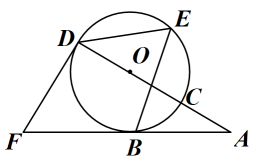 (1)、求∠DEB的度数;(2)、若⊙O的半径为2,点F在AB的延长线上,且BF=2 , 求证:DF与⊙O相切.20. 猕猴嬉戏是王屋山景区的一大特色,猕猴玩偶非常畅销.小李在某网店选中A,B两款猕猴玩偶,决定从该网店进货并销售.两款玩偶的进货价和销售价如下表:
(1)、求∠DEB的度数;(2)、若⊙O的半径为2,点F在AB的延长线上,且BF=2 , 求证:DF与⊙O相切.20. 猕猴嬉戏是王屋山景区的一大特色,猕猴玩偶非常畅销.小李在某网店选中A,B两款猕猴玩偶,决定从该网店进货并销售.两款玩偶的进货价和销售价如下表:类别
价格
A款玩偶
B款玩偶
进货价(元/个)
40
30
销售价(元/个)
56
45
(1)、第一次小李用1100元购进了A,B两款玩偶共30个,求两款玩偶各购进多少个?(2)、第二次小李进货时,网店规定A款玩偶进货数量不得超过B款玩偶进货数量的一半.小李计划购进两款玩偶共30个,应如何设计进货方案才能获得最大利润,最大利润是多少?21. 阅读理解:如图1,若一个四边形的两条对角线互相垂直,则称这个四边形为垂美四边形. (1)、概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由;(2)、性质探究:如图1,试在垂美四边形ABCD中探究AB2 , CD2 , AD2 , BC2之间的关系,并说明理由;(3)、解决问题:如图3,分别以Rt△ABC的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结CE、BG、GE、CE交BG于点N,交AB于点M.已知AC= , AB=2,求GE的长.22. 综合与探究:如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(-1,0),B(3,0),C(0,-4)三点,点P(m,n)是直线BC下方抛物线上的一个动点.
(1)、概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由;(2)、性质探究:如图1,试在垂美四边形ABCD中探究AB2 , CD2 , AD2 , BC2之间的关系,并说明理由;(3)、解决问题:如图3,分别以Rt△ABC的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结CE、BG、GE、CE交BG于点N,交AB于点M.已知AC= , AB=2,求GE的长.22. 综合与探究:如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(-1,0),B(3,0),C(0,-4)三点,点P(m,n)是直线BC下方抛物线上的一个动点.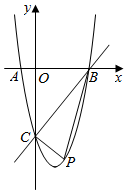 (1)、求这个二次函数的解析式;(2)、动点P运动到什么位置时,△PBC的面积最大,求出此时P点坐标及△PBC面积的最大值;(3)、在y轴上是否存在点Q,使以O,B,Q为顶点的三角形与△AOC相似?若存在,请写出点Q的坐标;若不存在,请说明理由.
(1)、求这个二次函数的解析式;(2)、动点P运动到什么位置时,△PBC的面积最大,求出此时P点坐标及△PBC面积的最大值;(3)、在y轴上是否存在点Q,使以O,B,Q为顶点的三角形与△AOC相似?若存在,请写出点Q的坐标;若不存在,请说明理由.