山东省济南市高新区2022年一模数学试题

试卷更新日期：2022-04-15 类型：中考模拟

进入出卷网下载

一、单选题

1. 5的相反数是（）

A、5 B、﹣5 C、5或﹣5 D、 $\frac{1}{5}$

查看试题解析
2. 如图所示的几何体，其主视图是（）

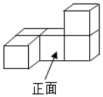A、 B、 C、 D、

查看试题解析
3. 2021年10月16日，神舟十三号载人飞船顺利将三位宇航员送入太空，飞船平均飞行速度为每小时28440000米，用科学记数法表示28440000为（）

A、2.844×10⁷ B、2.844×10⁸ C、28.44×10⁷ D、0.2844×10⁸

查看试题解析
4. 如图，直线 $l_{1} ∥ l_{2}$ 被直线 $l_{3}$ 所截， $∠ 1 = ∠ 2 = 36 °$ ， $∠ P = 90 °$ ，则 $∠ 3 =$ （）．

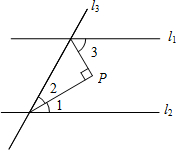A、36° B、54° C、46° D、44°

查看试题解析
5. 下列计算正确的是（　　）

A、a²+a³＝a⁵ B、a³•a³＝a⁹ C、（a³）²＝a⁶ D、（ab）²＝ab²

查看试题解析
6. 窗花是我国传统民间艺术，下列窗花中，是轴对称图形的为（）

A、 B、 C、 D、

查看试题解析
7. 计算 $\frac{x}{a + 1} \cdot \frac{a^{2} - 1}{2 x}$ 的结果正确的是（）

A、 $\frac{a - 1}{2}$ B、 $\frac{a + 1}{2}$ C、 $\frac{a - 1}{2 x}$ D、 $\frac{a + 1}{2 a + 2}$

查看试题解析
8. 如图A是某公园的进口，B，C，D是三个不同的出口，小明从A处进入公园，那么从B，C，D三个出口中恰好在C出口出来的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
9. 一次函数y＝mx﹣n（m，n为常数）的图象如图所示，则不等式mx﹣n≥0的解集是（）

A、x≥2 B、x≤2 C、x≥3 D、x≤3

查看试题解析
10. 如图钓鱼竿AC长6m，露在水面上的鱼线BC长3 $\sqrt{2}$ m，钓者想看看鱼钓上的情况，把鱼竿AC逆时针转动15°到AC′的位置，此时露在水面上的鱼线B'C'长度是（）

A、3m B、 $3 \sqrt{3}$ m C、 $2 \sqrt{3}$ m D、4m

查看试题解析
11. 如图，在Rt△ABC中，∠B＝90°，AB＝8，BC＝6，延长BC至E，使得CE＝BC，将△ABC沿AC翻折，使点B落点D处，连接DE，则DE的长为（）

A、 $\frac{18}{5}$ B、 $\frac{24}{5}$ C、 $\frac{32}{5}$ D、 $\frac{36}{5}$

查看试题解析
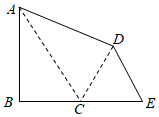12. 对于一个函数：当自变量x取a时，其函数值y也等于a，我们称a为这个函数的不动点．若二次函数y＝x²+2x+c（c为常数）有两个不相等且都小于1的不动点，则c的取值范围是（）

A、 $c < - 3$ B、 $- 3 < c < - 2$ C、 $- 2 < c < \frac{1}{4}$ D、 $c > - \frac{1}{4}$

查看试题解析

二、填空题

13. 因式分解：1-2x+x²= ．

查看试题解析
14. 如图，随机闭合开关S₁、S₂、S₃中的两个，则灯泡发光的概率为．

查看试题解析
15. 如图，在正六边形ABCDEF中，连接DA、DF，则 $\frac{D F}{D A}$ 的值为．

查看试题解析
16. 已知x=m是一元二次方程x²−x−1=0的一个根，则代数式m²−m+2021的值为．

查看试题解析
17. 一个横断面是抛物线的渡槽如图所示，根据图中所给的数据求出水面的宽度是cm．

查看试题解析
18. 如图，已知正方形ABCD，延长AB至点E使BE＝AB，连接CE、DE，DE与BC交于点N，取CE的中点F，连接BF，AF，AF交BC于点M，交DE于点O，则下列结论：①DN＝EN；②OA＝OE；③tan∠CED $= \frac{1}{3}$ ；④S_四_边_形BEFM＝2S△_CMF ．其中正确的是．（只填序号）

查看试题解析

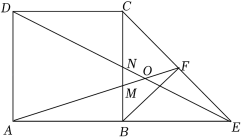
三、解答题

19. 计算： $2^{- 1} + 4 c o s 45 ° - \sqrt{8} + {(π - 2022)}^{0}$

查看试题解析
20. 解不等式组 ${\begin{array}{l} 2 (x + 1) > 1 \\ \frac{x - 1}{2} < 1 \end{array}$ ，求出解集并写出此不等式组的整数解．

查看试题解析
21. 如图，四边形ABCD是平行四边形，E为BC的中点，连接AE交DC延长线于点F．求证：DC＝CF．

查看试题解析
22. 某校要加强中小学生作业、睡眠、手机、读物、体质管理．数学社团成员采用随机抽样的方法，抽取了七年级若干名学生，对他们一周内平均每天的睡眠时间t（单位：h）进行了调查，将数据整理后得到下列不完整的统计图表和扇形统计图：
组别
睡眠时间分组
频数
A
t＜6
4
B
6≤t＜7
8
C
7≤t＜8
10
D
8≤t＜9
21
E
t≥9
m
请根据图表信息回答下列问题：

(1)、本次被抽取的七年级学生共有名；

(2)、统计图表中，m＝；

(3)、扇形统计图中，C组所在扇形的圆心角的度数是°；

(4)、请估计该校800名七年级学生中睡眠不足7小时的人数．

查看试题解析
23. 如图，AB为⊙O的直径，C为⊙O上一点，经过点C的切线交AB的延长线于点E ， $A D ⊥ E C$ 交EC的延长线于点D，连接AC .

(1)、求证： AC平分∠DAE ；

(2)、若 $c o s ∠ D A E = \frac{2}{3} ， B E = 2$ ，求⊙O的半径.

查看试题解析
24. 为了防控“新冠肺炎”疫情，某校积极进行校园环境消毒，购买了甲、乙两种消毒液共100瓶，其中甲种8元/瓶，乙种12元/瓶．

(1)、如果购买这两种消毒液共用1040元，求甲，乙两种消毒液各购买多少瓶？

(2)、该校准备再次购买这两种消毒液（不包括已购买的100瓶），使乙种瓶数是甲种瓶数的2倍少4瓶，且所需费用不多于1200元，求甲种消毒液最多能再购买多少瓶？

查看试题解析
25. 如图，在平面直角坐标系 $x O y$ 中，一次函数 $y = k_{1} x + b$ 的图象与反比例函数 $y = \frac{k_{2}}{x}$ 的图象交于点 $A (2 ， 4)$ 和点 $B (m ， - 2)$ ．

(1)、求一次函数与反比例函数的表达式；

(2)、直线 $A B$ 与 $x$ 轴交于点 $D$ ，与 $y$ 轴交于点 $C$ ．
①过点 $C$ 作 $C E / / x$ 轴交反比例函数 $y = \frac{k_{2}}{x}$ 的图象于点 $E$ ，连接 $A E$ ，试判断 $Δ A C E$ 的形状，并说明理由；
②设 $M$ 是 $x$ 轴上一点，当 $∠ C M O = \frac{1}{2} ∠ D C O$ 时，求点 $M$ 的坐标．

查看试题解析
26. 如图，△ABC和△ADE是有公共顶点的直角三角形，∠BAC＝∠DAE＝90°，点P为射线BD，CE的交点．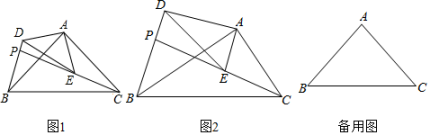

(1)、如图1，若△ABC和△ADE是等腰三角形，猜想∠ABD和∠ACE的数量关系是 ▲ ，并说明理由；

(2)、如图2，若∠ADE＝∠ABC＝30°，则（1）中的结论是否仍然成立成立？请说明理由．

(3)、在（1）的条件下，AB＝6，AD＝4，若把△ADE绕点A旋转，当∠EAC＝90°时，请直接写出PB的长度．

查看试题解析
27. 如图，在平面直角坐标系中，抛物线y $= - \frac{1}{2} x^{2} +$ bx+c与x轴交于A（﹣2，0）、B（4，0）两点（点A在点B的左侧），与y轴交于点C，连接AC、BC，点P为直线BC上方抛物线上一动点，连接OP交BC于点Q．

(1)、求抛物线的函数表达式；

(2)、当 $\frac{P Q}{O Q}$ 的值最大时，求点P的坐标和 $\frac{P Q}{O Q}$ 的最大值；

(3)、把抛物线y $= - \frac{1}{2} x^{2} +$ bx+c沿射线AC方向平移 $\sqrt{5}$ 个单位得新抛物线y'，M是新抛物线上一点，N是新抛物线对称轴上一点，当以M、N、B、C为顶点的四边形是平行四边形时，直接写出N点的坐标．

查看试题解析

组别	睡眠时间分组	频数
A	t＜6	4
B	6≤t＜7	8
C	7≤t＜8	10
D	8≤t＜9	21
E	t≥9	m