山东省菏泽市曹县2022年中考一模数学试题
试卷更新日期:2022-04-15 类型:中考模拟
一、单选题
-
1. 下列实数中,最小的数是( )A、-2 B、 C、0 D、2. 某种计算机完成一次基本运算的时间约为0.0000000015秒,数字0.0000000015用科学记数法表示为( )A、1.5×10﹣7 B、1.5×10﹣8 C、1.5×10﹣9 D、1.5×10﹣103. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 若关于x的一元二次方程x2﹣2x+m=0没有实数根,则m的值可以是( )A、﹣1 B、0 C、1 D、5. 如图,在 中, ,分别以点 为圆心, 的长为半径作弧,两弧交于点D,连接 则四边形 的面积为( )
4. 若关于x的一元二次方程x2﹣2x+m=0没有实数根,则m的值可以是( )A、﹣1 B、0 C、1 D、5. 如图,在 中, ,分别以点 为圆心, 的长为半径作弧,两弧交于点D,连接 则四边形 的面积为( ) A、 B、9 C、6 D、6. 某校九年级一班准备举行一次演讲比赛,甲、乙、丙三人通过抽签的方式决定出场顺序,则出场顺序恰好是甲、乙、丙的概率为( )A、 B、 C、 D、7. 如图,在菱形中,点分别是边的中点,连接 . 若菱形的面积为8,则的面积为( )
A、 B、9 C、6 D、6. 某校九年级一班准备举行一次演讲比赛,甲、乙、丙三人通过抽签的方式决定出场顺序,则出场顺序恰好是甲、乙、丙的概率为( )A、 B、 C、 D、7. 如图,在菱形中,点分别是边的中点,连接 . 若菱形的面积为8,则的面积为( ) A、2 B、3 C、4 D、58. 二次函数y=ax2﹣2ax+c(a>0)的图象经过点A(﹣3,y1),B(﹣1,y2),C(2,y3),D(4,y4)四个点,若y2y4<0,则下列结论正确的是( )A、y1y3>0 B、y1y3≥0 C、y1y3<0 D、y1y3≤0
A、2 B、3 C、4 D、58. 二次函数y=ax2﹣2ax+c(a>0)的图象经过点A(﹣3,y1),B(﹣1,y2),C(2,y3),D(4,y4)四个点,若y2y4<0,则下列结论正确的是( )A、y1y3>0 B、y1y3≥0 C、y1y3<0 D、y1y3≤0二、填空题
-
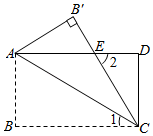
9. 已知: ,则 .10. 如图,将矩形ABCD沿AC折叠,使点B落在点B'处,B'C交AD于点E,若∠1=25°,则∠2的度数为 .
 11. 已知则的值为 .12. 如图,在▱ABCD中,AB=10,AD=6,AC⊥BC,交BD于点O,则BD的长为 .
11. 已知则的值为 .12. 如图,在▱ABCD中,AB=10,AD=6,AC⊥BC,交BD于点O,则BD的长为 .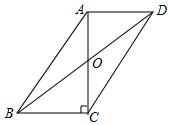 13. 如图,△ABC中,∠C=90°,AC=BC , 将△ABC绕点A顺时针方向旋转60°到△AB'C'的位置,连接BC',BC'的延长线交AB'于点D,则BD的长为 .
13. 如图,△ABC中,∠C=90°,AC=BC , 将△ABC绕点A顺时针方向旋转60°到△AB'C'的位置,连接BC',BC'的延长线交AB'于点D,则BD的长为 .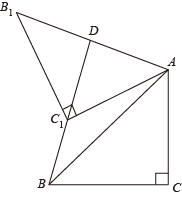 14. 如图,正方形 的边长为4, 的半径为1.若 在正方形 内平移( 可以与该正方形的边相切),则点A到 上的点的距离的最大值为.
14. 如图,正方形 的边长为4, 的半径为1.若 在正方形 内平移( 可以与该正方形的边相切),则点A到 上的点的距离的最大值为.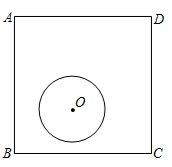
三、解答题
-
15. 计算:()0﹣6cos30°+()-2 .16. 先化简,再求值:(a+1) , 其中a .17. 如图,∠BAC=90°,AB=AC,BE⊥AD于点E,CF⊥AD于点F,求证:AF=BE.
 18. 如图,某海岸线MN的方向为北偏东75°,甲,乙两船分别向海岛C运送物资,甲船从港口A处沿北偏东45°方向航行,乙船从港口B处沿北偏东30°方向航行,已知港口B到海岛C的距离为30海里,求港口A到海岛C的距离.
18. 如图,某海岸线MN的方向为北偏东75°,甲,乙两船分别向海岛C运送物资,甲船从港口A处沿北偏东45°方向航行,乙船从港口B处沿北偏东30°方向航行,已知港口B到海岛C的距离为30海里,求港口A到海岛C的距离. 19. 为了有效推进儿童青少年近视防控工作,某校积极落实教育部办公厅等十五部门联合制定《儿童青少年近视防控光明行动工作方案》,决定开设以下四种球类的课外选修课程:篮球、足球、排球、乒乓球,为了解学生需求,该校随机对本校部分学生进行了“你选择哪种球类课程”的调查(要求必须选择且只能选择其中一门课程),并根据调查结果绘制成如下不完整的统计图表.
19. 为了有效推进儿童青少年近视防控工作,某校积极落实教育部办公厅等十五部门联合制定《儿童青少年近视防控光明行动工作方案》,决定开设以下四种球类的课外选修课程:篮球、足球、排球、乒乓球,为了解学生需求,该校随机对本校部分学生进行了“你选择哪种球类课程”的调查(要求必须选择且只能选择其中一门课程),并根据调查结果绘制成如下不完整的统计图表.课程
人数
篮球
m
足球
21
排球
30
兵乓球
n
 (1)、求m,n的值;(2)、求扇形统计图中“足球”对应扇形圆心角的度数;(3)、该校共有1800名学生,请你估计全校选择“乒乓球”课程的学生人数.20. 如图,一次函数y1=kx+b(k≠0)的图象与x轴、y轴分别交于A、B两点,与反比例函数y2(n≠0)的图象在第二象限交于点C,CD⊥x轴于点D,OB=2OA,AB=3 , CD=10.
(1)、求m,n的值;(2)、求扇形统计图中“足球”对应扇形圆心角的度数;(3)、该校共有1800名学生,请你估计全校选择“乒乓球”课程的学生人数.20. 如图,一次函数y1=kx+b(k≠0)的图象与x轴、y轴分别交于A、B两点,与反比例函数y2(n≠0)的图象在第二象限交于点C,CD⊥x轴于点D,OB=2OA,AB=3 , CD=10. (1)、求一次函数与反比例函数的表达式;(2)、当x<0时,比较y1 , y2的大小.21. 某地遭遇强降雨,引发洪涝灾害,人民的生活受到了极大的影响.某市筹集了大量的生活物资,用A,B两种型号的货车,分两批运往受灾严重的地区.具体运输情况如表:
(1)、求一次函数与反比例函数的表达式;(2)、当x<0时,比较y1 , y2的大小.21. 某地遭遇强降雨,引发洪涝灾害,人民的生活受到了极大的影响.某市筹集了大量的生活物资,用A,B两种型号的货车,分两批运往受灾严重的地区.具体运输情况如表:第一批
第二批
A种型号货车的辆数
1
2
B种型号货车的辆数
3
5
累计运送物资的吨数
28
50
(1)、求A,B两种型号的货车每辆分别能运多少吨生活物资?(2)、该市后续又筹集了62.4吨生活物资,现已联系了3辆A种型号的货车.试问至少还需要联系多少辆B种型号货车?才能一次将这批生活物资运往目的地.22. 如图,AB是⊙O的直径,点C是⊙O上一点,连接AC,BC,点D在BA的延长线上,∠DCA=∠ABC,BE⊥DC,交DC的延长线于点E. (1)、求证:DC是⊙O的切线;(2)、若 , BE=6,求AD的长.23. 如图,正方形ABCD中,点E是BC边上一点,点F是BA延长线上一点,AF=CE,连接EF,交AD于点K,过点D作DH⊥EF,垂足为点H,延长DH交BF于点G,连接HC,HB.
(1)、求证:DC是⊙O的切线;(2)、若 , BE=6,求AD的长.23. 如图,正方形ABCD中,点E是BC边上一点,点F是BA延长线上一点,AF=CE,连接EF,交AD于点K,过点D作DH⊥EF,垂足为点H,延长DH交BF于点G,连接HC,HB.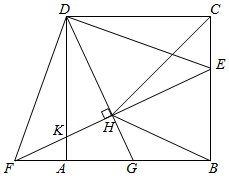 (1)、求证:HDEF;(2)、若DK•HC=4 , 求HE的长.24. 如图,抛物线y=ax2+bx﹣3与x轴相交于B(﹣1,0),C(3,0)两点.
(1)、求证:HDEF;(2)、若DK•HC=4 , 求HE的长.24. 如图,抛物线y=ax2+bx﹣3与x轴相交于B(﹣1,0),C(3,0)两点.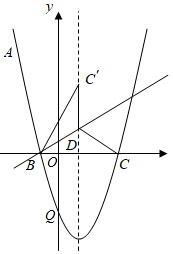 (1)、求抛物线的函数表达式;(2)、抛物线的对称轴与x轴的交点为H,点D在抛物线的对称轴上,且位于x轴的上方,将△BCD沿直线BD翻折得到△BC'D,若点C'恰好落在抛物线的对称轴上,求点C',D的坐标;(3)、设点P在抛物线上,位于对称轴右侧且在x轴的上方,点Q在抛物线的对称轴上,当△CPQ为等边三角形时,求直线BP的函数表达式.
(1)、求抛物线的函数表达式;(2)、抛物线的对称轴与x轴的交点为H,点D在抛物线的对称轴上,且位于x轴的上方,将△BCD沿直线BD翻折得到△BC'D,若点C'恰好落在抛物线的对称轴上,求点C',D的坐标;(3)、设点P在抛物线上,位于对称轴右侧且在x轴的上方,点Q在抛物线的对称轴上,当△CPQ为等边三角形时,求直线BP的函数表达式.