山东省东明县2022年九年级中考第一次模拟数学试题
试卷更新日期:2022-04-15 类型:中考模拟
一、单选题
-
1. 下面四个几何体中,左视图为圆形的是( )A、
 B、
B、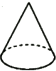 C、
C、 D、
D、 2. 矩形具有而菱形不具有的性质是( )A、两组对边分别相等 B、两组对边分别平行 C、两条对角线相等 D、两条对角线互相垂直3. 直线不经过第二象限,则关于x的方程实数解的个数是( )A、0个或1个 B、0个或2个 C、1个或2个 D、0个或1个或2个4. 以下说法合理的是( )A、小明做了3次掷图钉的实验,发现1次钉尖朝上,由此他说钉尖朝上的概率是 B、小明做了3次掷均匀硬币的实验,其中有一次正面朝上,2次正面朝下,他认为再掷一次,正面朝上的概率还是 C、某射击运动员射击一次只有两种可能的结果:中靶与不中靶,所以他击中靶的概率是 D、某彩票的中奖概率是5%,那么买1000张彩票一定有50张中奖5. 一个扇形的半径为3,圆心角为40°,则该扇形的面积是( )A、 B、 C、 D、6. 如图,将以O为位似中心,扩大到 , 各点坐标分别为 , , , 则点C的坐标为( )
2. 矩形具有而菱形不具有的性质是( )A、两组对边分别相等 B、两组对边分别平行 C、两条对角线相等 D、两条对角线互相垂直3. 直线不经过第二象限,则关于x的方程实数解的个数是( )A、0个或1个 B、0个或2个 C、1个或2个 D、0个或1个或2个4. 以下说法合理的是( )A、小明做了3次掷图钉的实验,发现1次钉尖朝上,由此他说钉尖朝上的概率是 B、小明做了3次掷均匀硬币的实验,其中有一次正面朝上,2次正面朝下,他认为再掷一次,正面朝上的概率还是 C、某射击运动员射击一次只有两种可能的结果:中靶与不中靶,所以他击中靶的概率是 D、某彩票的中奖概率是5%,那么买1000张彩票一定有50张中奖5. 一个扇形的半径为3,圆心角为40°,则该扇形的面积是( )A、 B、 C、 D、6. 如图,将以O为位似中心,扩大到 , 各点坐标分别为 , , , 则点C的坐标为( ) A、 B、 C、 D、7. 已知反比例函数 , 则下列说法正确的是( )A、y随x的增大而减小 B、y随x的增大而增大 C、y随x的增大保持不变 D、图象在第一、三象限8. 如图,在中, , , , 则的面积是( )
A、 B、 C、 D、7. 已知反比例函数 , 则下列说法正确的是( )A、y随x的增大而减小 B、y随x的增大而增大 C、y随x的增大保持不变 D、图象在第一、三象限8. 如图,在中, , , , 则的面积是( ) A、 B、 C、 D、9. 已知平面内有⨀O和点A,B,若⨀O的半径为2cm,线段OA=3cm,OB=2cm,则直线AB与⨀O 的位置关系为( )A、相交 B、相切 C、相交或相切10. 已知在同一直角坐标系中,二次函数y= ax2+bx和反比例函数y=的图象如图所示,则一次函数y=x+b的图象可能是( )
A、 B、 C、 D、9. 已知平面内有⨀O和点A,B,若⨀O的半径为2cm,线段OA=3cm,OB=2cm,则直线AB与⨀O 的位置关系为( )A、相交 B、相切 C、相交或相切10. 已知在同一直角坐标系中,二次函数y= ax2+bx和反比例函数y=的图象如图所示,则一次函数y=x+b的图象可能是( )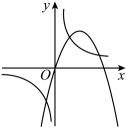 A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
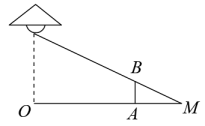
11. 据统计,上海学生人数每年以较快的幅度增长,2019年的学生人数是15万人,2021年的学生人数达到23万人,设平均年增长率为x,则根据题意,可列方程 .12. 若点 , 在同一个反比例函数的图象上,则m的值为 .13. 抛物线经过点、两点,则关于x的一元二次方程的解是 .14. 如图,路灯距离地面6米,身高1.2米的小明站在距离路灯的底部(点O)10米的A处,则小明的影长为米.
 15. 如图,正方形ABCD的边长为6cm,则图中阴影部分的面积为cm2 .
15. 如图,正方形ABCD的边长为6cm,则图中阴影部分的面积为cm2 . 16. 如图,A,B,C,D是⊙上的四个点, , 则度.
16. 如图,A,B,C,D是⊙上的四个点, , 则度. 17. 如图,CD是⊙的直径,AB是弦, , 若 , , 则AC的长为 .
17. 如图,CD是⊙的直径,AB是弦, , 若 , , 则AC的长为 . 18. 如图,等边被一平行于BC的矩形所截,AB被截成三等份,若的面积为12cm2 , 图中阴影部分的面积为cm2 .
18. 如图,等边被一平行于BC的矩形所截,AB被截成三等份,若的面积为12cm2 , 图中阴影部分的面积为cm2 .
三、解答题
-
19.(1)、解方程: .(2)、计算: .20. 如图,在中, , 延长CB到点E,使 , 连接AE.
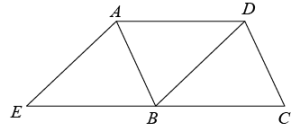 (1)、求证:四边形AEBD是菱形;(2)、连接DE交AB于点F,若 , , 求AD的长.21. 全面两孩政策实施后,甲、乙两个家庭有了各自的规划,假定生男生女的概率相同,回答下列问题:(1)、甲家庭已有一个男孩,准备再生一个孩子,则第二个孩子是男孩的概率是;(2)、乙家庭没有孩子,准备生两个孩子,求有一个男孩一个女孩的概率.22. 为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时60海里的速度向正东方航行,在A处测得灯塔P在北偏东60°方向上;继续航行1小时到达B处,此时测得灯塔P在北偏东30°方向上.
(1)、求证:四边形AEBD是菱形;(2)、连接DE交AB于点F,若 , , 求AD的长.21. 全面两孩政策实施后,甲、乙两个家庭有了各自的规划,假定生男生女的概率相同,回答下列问题:(1)、甲家庭已有一个男孩,准备再生一个孩子,则第二个孩子是男孩的概率是;(2)、乙家庭没有孩子,准备生两个孩子,求有一个男孩一个女孩的概率.22. 为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时60海里的速度向正东方航行,在A处测得灯塔P在北偏东60°方向上;继续航行1小时到达B处,此时测得灯塔P在北偏东30°方向上.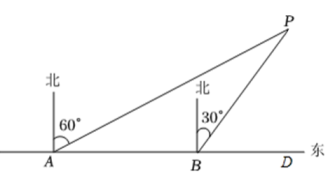 (1)、求的度数;(2)、已知在灯塔P的周围30海里内有暗礁,问海监船继续向正东方向航行是否安全?
(1)、求的度数;(2)、已知在灯塔P的周围30海里内有暗礁,问海监船继续向正东方向航行是否安全?

