辽宁省葫芦岛市2022年六校联考第二次模拟数学试题
试卷更新日期:2022-04-15 类型:中考模拟
一、单选题
-
1. 下面四个数中,分数是( )A、3 B、 C、 D、2. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
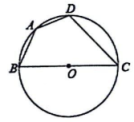
D、 3. 估计 ﹣1的值在( )A、1到2之间 B、2到3之间 C、3到4之间 D、4到5之间4. 下列运算正确的是( )A、 B、 C、 D、5. 甲、乙两人在相同条件下进行射击练习,每人10次射击成绩的平均数都是8环,方差分别为 , 则两人射击成绩波动情况是( )A、甲波动大 B、乙波动大 C、甲、乙波动一样 D、无法比较6. 下列事件中,是必然事件的是( )A、抛掷一个骰子,出现8点朝上 B、三角形的内角和是 C、汽车经过一个有红绿灯的路口时,前方恰好是绿灯 D、明天考试,小明会考满分7. 若一次函数的图象向下平移3个单位后经过点 , 则b的值为( )A、3 B、4 C、5 D、68. 如图,为直径,点A,D在上, , 若 , 则的长为( )
3. 估计 ﹣1的值在( )A、1到2之间 B、2到3之间 C、3到4之间 D、4到5之间4. 下列运算正确的是( )A、 B、 C、 D、5. 甲、乙两人在相同条件下进行射击练习,每人10次射击成绩的平均数都是8环,方差分别为 , 则两人射击成绩波动情况是( )A、甲波动大 B、乙波动大 C、甲、乙波动一样 D、无法比较6. 下列事件中,是必然事件的是( )A、抛掷一个骰子,出现8点朝上 B、三角形的内角和是 C、汽车经过一个有红绿灯的路口时,前方恰好是绿灯 D、明天考试,小明会考满分7. 若一次函数的图象向下平移3个单位后经过点 , 则b的值为( )A、3 B、4 C、5 D、68. 如图,为直径,点A,D在上, , 若 , 则的长为( )
 A、2 B、1 C、 D、9. 在育红学校开展的课外阅读活动中,学生人均阅读量从七年级的每年100万字增加到九年级的每年121万字.设该校七至九年级人均阅读量年均增长率为x , 根据题意,所列方程正确的是( )A、 B、 C、 D、10. 如图, , 垂足为点B,平分 , 点A从点B出发,沿射线运动,连接交于点C,设的面积为y,则下列图象中能大致反映y与x的函数关系的图象是( )
A、2 B、1 C、 D、9. 在育红学校开展的课外阅读活动中,学生人均阅读量从七年级的每年100万字增加到九年级的每年121万字.设该校七至九年级人均阅读量年均增长率为x , 根据题意,所列方程正确的是( )A、 B、 C、 D、10. 如图, , 垂足为点B,平分 , 点A从点B出发,沿射线运动,连接交于点C,设的面积为y,则下列图象中能大致反映y与x的函数关系的图象是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 某地积极响应党中央号召,大力推进农村厕所革命,已经累计投资110200000元资金.数据110200000用科学记数法可表示为 .12. 方程组的解是 .13. 函数中,自变量x的取值范围是 .14. 不透明袋子中装有黑球1个、白球2个,这些球除了颜色外无其他差别.从袋子中随机摸出一个球,记下颜色后放回,将袋子中的球摇匀,再随机摸出一个球,记下颜色,前后两次摸出的球都是白球的概率是.15. 如图,中, , 点D在边上,以为折痕将折叠,得到 , 若 , 则的长为 .
 16. 如图,矩形的对角线交于点O,点A,C在y轴上,交x轴于点E, , , 反比例函数的图象经过点D,则k的值为 .
16. 如图,矩形的对角线交于点O,点A,C在y轴上,交x轴于点E, , , 反比例函数的图象经过点D,则k的值为 .
三、解答题
-
17. 如图,中, , 分别以A,C为圆心,大于长为半径作弧,两弧交于点D,点E,直线与交交于点F,交于点G,与交于点H,若 , 则的长为 .
 18. 如图,正方形的边长为4,点E是对角线上的动点(点E不与A,C重合),连接交于点F,线段绕点F逆时针旋转得到线段 , 连接 . 下列结论:①;②;③若四边形的面积是正方形面积的一半,则的长为;④ . 其中正确的是 . (填写所有正确结论的序号)
18. 如图,正方形的边长为4,点E是对角线上的动点(点E不与A,C重合),连接交于点F,线段绕点F逆时针旋转得到线段 , 连接 . 下列结论:①;②;③若四边形的面积是正方形面积的一半,则的长为;④ . 其中正确的是 . (填写所有正确结论的序号) 19. 先化简,再求值:÷(x+1﹣),其中x=﹣2.20. 为迎接2022年北京冬奥会,冬奥组委准备印发一些宣传海报,某印刷厂由甲、乙两台机器印刷,甲机器的印刷效率是乙机器的倍,甲机器印刷360份比乙机器印刷同样数量少3分钟.(1)、甲、乙两台机器每分钟能印刷多少份宣传海报?(2)、若甲、乙两台机器同时印刷,为保证印刷的宣传海报不少于5000份,两台机器至少应印刷多长时间?21. 2021年,为了能源资源配置更加合理,我国多地发布限电令.某校为了解学生对限电原因的了解程度,在九年级学生中作了一次抽样调查,并将结果分成四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查结果绘制成了如下不完整的统计图:
19. 先化简,再求值:÷(x+1﹣),其中x=﹣2.20. 为迎接2022年北京冬奥会,冬奥组委准备印发一些宣传海报,某印刷厂由甲、乙两台机器印刷,甲机器的印刷效率是乙机器的倍,甲机器印刷360份比乙机器印刷同样数量少3分钟.(1)、甲、乙两台机器每分钟能印刷多少份宣传海报?(2)、若甲、乙两台机器同时印刷,为保证印刷的宣传海报不少于5000份,两台机器至少应印刷多长时间?21. 2021年,为了能源资源配置更加合理,我国多地发布限电令.某校为了解学生对限电原因的了解程度,在九年级学生中作了一次抽样调查,并将结果分成四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查结果绘制成了如下不完整的统计图: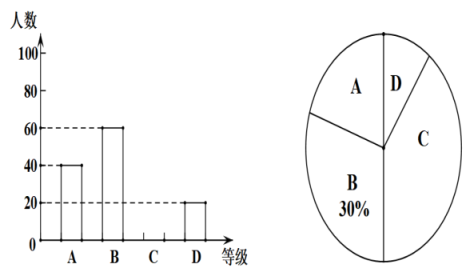
请根据图中信息回答下列问题:
(1)、本次被调查的学生有 ▲ 人;请补全条形统计图;(2)、若该校九年级共有1200名学生,请你估计该校九年级学生中“比较了解”限电原因的学生有多少人?(3)、九年(1)班被查的学生中A等级的有5人,其中2名男生,3名女生,现打算从这5名学生中随意抽取2人进行电话采访,请用列表或画树状图的方法求恰好抽到一男一女的概率.22. 如图,是的直径,是的内接三角形, , 与交于点E,过点C作交的延长线于点F. (1)、求证:是的切线;(2)、若半径为5, , 求线段的长.23. 为了维护我国海域安全,某巡逻艇从码头A出发向东航行40海里后到达B处,再从B处沿北偏东方向行驶40海里到达C处,然后沿北偏西方向航行到D处,发现码头A在正南方向.求此时巡逻艇与码头A的距离.
(1)、求证:是的切线;(2)、若半径为5, , 求线段的长.23. 为了维护我国海域安全,某巡逻艇从码头A出发向东航行40海里后到达B处,再从B处沿北偏东方向行驶40海里到达C处,然后沿北偏西方向航行到D处,发现码头A在正南方向.求此时巡逻艇与码头A的距离. 24. 小明购进一些糖果,把这些糖果进行包装后销售,包装后每千克售价为30元,已知购进糖果的总价(元)与数量x(千克)之间满足如图所示的二次函数 , 这些糖果的包装总费用(元)与数量x(千克)满足一次函数 .
24. 小明购进一些糖果,把这些糖果进行包装后销售,包装后每千克售价为30元,已知购进糖果的总价(元)与数量x(千克)之间满足如图所示的二次函数 , 这些糖果的包装总费用(元)与数量x(千克)满足一次函数 . (1)、求与x之间的函数关系式;(2)、若小明购进的糖果不少于8千克且不多于10千克,他最多能获得多少利润?最少能获得多少利润?
(1)、求与x之间的函数关系式;(2)、若小明购进的糖果不少于8千克且不多于10千克,他最多能获得多少利润?最少能获得多少利润?

