辽宁省抚顺市顺城区2022年初中毕业生第一次质量调查数学试题
试卷更新日期:2022-04-15 类型:中考模拟
一、单选题
-
1. 下列方程是一元二次方程的是( )A、 B、 C、 D、2. 在下列四个图案中,是轴对称图形但不是中心对称图形的是( )A、
 B、
B、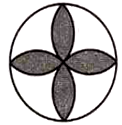 C、
C、 D、
D、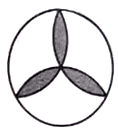 3. 下列事件中,是必然事件的是( )A、掷一次骰子,向上一面的点数是2 B、买一张电影票座位号是奇数 C、菱形的对角线互相垂直 D、射击运动员射击一次,命中靶心4. 掷一枚质地均匀的硬币,前6次都是正面朝上,则掷第7次时正面朝上的概率是( )A、1 B、 C、 D、05. 如果在二次函数的表达式y=ax2+bx+c中,a>0,b<0,c<0,那么这个二次函数的图象可能是( )A、
3. 下列事件中,是必然事件的是( )A、掷一次骰子,向上一面的点数是2 B、买一张电影票座位号是奇数 C、菱形的对角线互相垂直 D、射击运动员射击一次,命中靶心4. 掷一枚质地均匀的硬币,前6次都是正面朝上,则掷第7次时正面朝上的概率是( )A、1 B、 C、 D、05. 如果在二次函数的表达式y=ax2+bx+c中,a>0,b<0,c<0,那么这个二次函数的图象可能是( )A、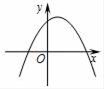 B、
B、 C、
C、 D、
D、 6. 若关于x的方程x2+x﹣m+ =0有实数根,则实数m的取值范围是( )A、m≥2 B、m≤2 C、m>2 D、m<27. 把抛物线的图象向右平移1个单位,再向上平移3个单位后,所得图象的函数表达式是( )A、 B、 C、 D、8. 如图,在△ABC中,∠BAC=90°,∠B=70°,将△ABC绕着点A逆时针旋转,得到△ADE,使得点D落在BC边上,过点E的直线l∥BC,则∠1=( )
6. 若关于x的方程x2+x﹣m+ =0有实数根,则实数m的取值范围是( )A、m≥2 B、m≤2 C、m>2 D、m<27. 把抛物线的图象向右平移1个单位,再向上平移3个单位后,所得图象的函数表达式是( )A、 B、 C、 D、8. 如图,在△ABC中,∠BAC=90°,∠B=70°,将△ABC绕着点A逆时针旋转,得到△ADE,使得点D落在BC边上,过点E的直线l∥BC,则∠1=( )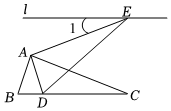 A、 B、 C、 D、9. 如图,点是的内心,的延长线和的外接圆相交于点 , 连接 , , , 若 , 则的大小为( )
A、 B、 C、 D、9. 如图,点是的内心,的延长线和的外接圆相交于点 , 连接 , , , 若 , 则的大小为( )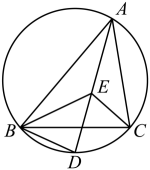 A、 B、 C、 D、10. 如图,抛物线( , , 为常数,)经过点 , 且对称轴为直线 , 有下列结论:①;②;③;④无论 , , 取何值,抛物线一定经过;⑤ , 其中正确结论的个数是( )
A、 B、 C、 D、10. 如图,抛物线( , , 为常数,)经过点 , 且对称轴为直线 , 有下列结论:①;②;③;④无论 , , 取何值,抛物线一定经过;⑤ , 其中正确结论的个数是( )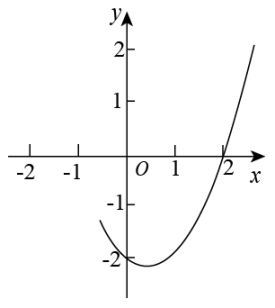 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
11. 方程3x=x2的根是 .12. 已知⊙O的半径为3,圆心O到直线L的距离为2,则直线L与⊙O的位置关系是.13. 设 分别为一元二次方程 的两个实数根,则 .14. 在如图所示的同心圆组成的盘面上投掷飞镖,飞镖落在阴影区域的概率是 .
 15. 如图,在△BOC中,∠COB=90°,OC=12,OB=5,将△BOC绕边OC所在直线旋转一周得到圆锥,则该圆锥的全面积是 .
15. 如图,在△BOC中,∠COB=90°,OC=12,OB=5,将△BOC绕边OC所在直线旋转一周得到圆锥,则该圆锥的全面积是 .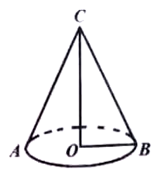 16. 要组织一次篮球赛,赛制为单循环形式(每两队之间都赛一场)计划安排15场比赛,应邀请个球队参加比赛.17. 如图,点在以为直径的半圆上, , , 点在线段上运动,点与点关于对称,于点 , 并交的延长线与点 . 下列结论:①;②;③线段的最小值为;④当时,与半圆相切;⑤当点从点运动到点时,线段扫过的面积是 . 其中正确的结论的序号为 .
16. 要组织一次篮球赛,赛制为单循环形式(每两队之间都赛一场)计划安排15场比赛,应邀请个球队参加比赛.17. 如图,点在以为直径的半圆上, , , 点在线段上运动,点与点关于对称,于点 , 并交的延长线与点 . 下列结论:①;②;③线段的最小值为;④当时,与半圆相切;⑤当点从点运动到点时,线段扫过的面积是 . 其中正确的结论的序号为 .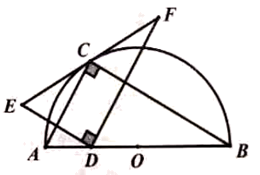
三、解答题
-
18. 如图,边长为4的等边三角形中,是对称轴上的一个动点,连接 , 将线段绕点顺时针旋转得到 , 连接 , 则在点运动过程中,的最小值是 .
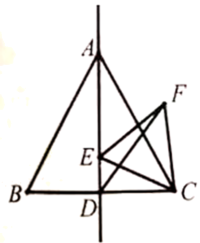 19. 解方程:(1)、(2)、20. 在如图所示平面直角坐标系中,每个小正方形的边长均为1,的三个顶点均在格点上.
19. 解方程:(1)、(2)、20. 在如图所示平面直角坐标系中,每个小正方形的边长均为1,的三个顶点均在格点上.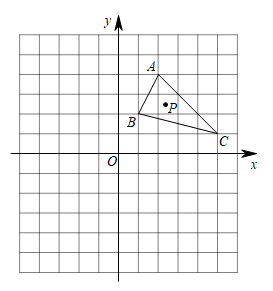
⑴将以为旋转中心逆时针旋转 , 画出旋转后的 , 并直接写出坐标 ▲ , ▲ , ▲ ;
⑵画出关于原点对称的 , 并直接写出坐标 ▲ , ▲ , ▲ ;
⑶若内有一点 , 经过上面两次变换后点在中的对应点为 , 请直接写出点的坐标 ▲ . (用含 , 的代数式表示)
21. 为庆祝中国共产党建党100周年,某校开展了党史知识竞赛.某年级随机选出了一个班的初赛成绩进行统计,得到如下统计图表,已知在扇形统计图分数段对应的扇形六圆心角为 . 某校组织读书征文比赛活动,评选出一、二、三等奖若干名,并绘成如图所示的统计表和扇形统计图(不完整),请你根据图中信息解答下列问题:统计表
分段
成绩范围(分)
频数
频率
90~100
0.1
80~89
20
70~79
0.3
70分以下
10
注:90~100表示成绩 , 满足 , 以下相同.
扇形统计图
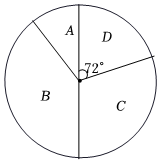 (1)、在统计表中, , , ;(2)、若该年级参加初赛的学生共有2000人,根据以上统计数据估计该年级成绩在90分及以上的学生人数;(3)、若统计表分数段的男生比女生少1人,从段中任选2人参加复赛,请用列表法或画树状图的方法,求出恰好抽到1名男生和1名女生的概率.22. 如图,将边长为40cm的正方形硬纸板的四个角各剪掉一个同样大小的正方形,剩余部分折成一个无盖的盒子.(纸板的厚度忽略不计).
(1)、在统计表中, , , ;(2)、若该年级参加初赛的学生共有2000人,根据以上统计数据估计该年级成绩在90分及以上的学生人数;(3)、若统计表分数段的男生比女生少1人,从段中任选2人参加复赛,请用列表法或画树状图的方法,求出恰好抽到1名男生和1名女生的概率.22. 如图,将边长为40cm的正方形硬纸板的四个角各剪掉一个同样大小的正方形,剩余部分折成一个无盖的盒子.(纸板的厚度忽略不计).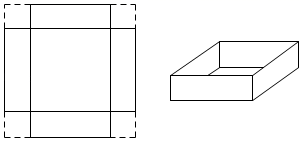 (1)、若该无盖盒子的底面积为900cm2 , 求剪掉的正方形的边长;(2)、求折成的无盖盒子的侧面积的最大值.23. 如图,是的内接三角形,是的直径,点在上,且 , 过点作的垂线与的延长线交于点 .
(1)、若该无盖盒子的底面积为900cm2 , 求剪掉的正方形的边长;(2)、求折成的无盖盒子的侧面积的最大值.23. 如图,是的内接三角形,是的直径,点在上,且 , 过点作的垂线与的延长线交于点 .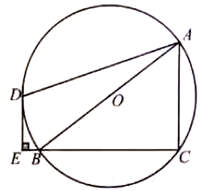 (1)、求证:是的切线;(2)、若 , , 求的半径.24. 经研究表明,某市跨河大桥上的车流速度V(单位:千米/时)是车流密度x(单位:辆/千米)的函数,函数图象如图所示.
(1)、求证:是的切线;(2)、若 , , 求的半径.24. 经研究表明,某市跨河大桥上的车流速度V(单位:千米/时)是车流密度x(单位:辆/千米)的函数,函数图象如图所示.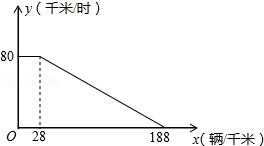 (1)、求当28≤x≤188时,关于x的函数表达式;(2)、求车流量P(单位:辆/时)与车流密度x之间的函数关系式;(注:车流量是单位时间内通过观测点的车辆数,计算公式为:车流量=车流速度×车流密度)(3)、若车流速度V不低于50千米时,求当车流密度x为多少时,车流量P达到最大,并求出这一最大值.25. 如图,中, , , , 垂足为 , 点在直线上,连接 , 将线段绕点逆时针旋转 , 得到线段 , 连接 , 直线与直线相交于点 .
(1)、求当28≤x≤188时,关于x的函数表达式;(2)、求车流量P(单位:辆/时)与车流密度x之间的函数关系式;(注:车流量是单位时间内通过观测点的车辆数,计算公式为:车流量=车流速度×车流密度)(3)、若车流速度V不低于50千米时,求当车流密度x为多少时,车流量P达到最大,并求出这一最大值.25. 如图,中, , , , 垂足为 , 点在直线上,连接 , 将线段绕点逆时针旋转 , 得到线段 , 连接 , 直线与直线相交于点 . (1)、连接 , 请直接写出线段与线段的数量关系;(2)、猜想线段与线段的数量关系,并说明理由;(3)、若 , , 请直接写出线段的长.26. 如图,抛物线的对称轴是x=1,与x轴交于点A,B(3,0),与y轴交于点C(0,3).
(1)、连接 , 请直接写出线段与线段的数量关系;(2)、猜想线段与线段的数量关系,并说明理由;(3)、若 , , 请直接写出线段的长.26. 如图,抛物线的对称轴是x=1,与x轴交于点A,B(3,0),与y轴交于点C(0,3).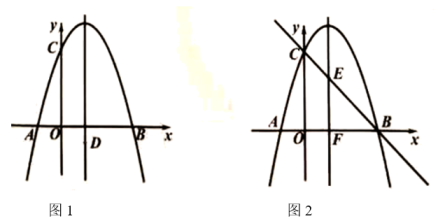 (1)、求抛物线的解析式;(2)、如图1,点在抛物线的对称轴上,连接 , 将线段以点为旋转中心顺时针旋转 , 得到线段 , 当点落在抛物线上,求出此时点的坐标;(3)、如图2,抛物线的对称轴与直线相交于点 , 于轴交于点 , 点在直线上,点在抛物线上,是否存在以 , , , 为顶点的四边形为平行四边形,若存在请直接写出点的坐标,若不存在请说明理由.
(1)、求抛物线的解析式;(2)、如图1,点在抛物线的对称轴上,连接 , 将线段以点为旋转中心顺时针旋转 , 得到线段 , 当点落在抛物线上,求出此时点的坐标;(3)、如图2,抛物线的对称轴与直线相交于点 , 于轴交于点 , 点在直线上,点在抛物线上,是否存在以 , , , 为顶点的四边形为平行四边形,若存在请直接写出点的坐标,若不存在请说明理由.